An infinite wire carries a current I. An S- shaped conducting rod of two semicircles esch of radius r is placed at an angle θ to the wire. The center of the conductor is at a distance d from the wire. If the rod translates parallel to the wire with a velocity v as shown in Fig. .3.56, calculate the emf induced across the ends Ob of the rod.

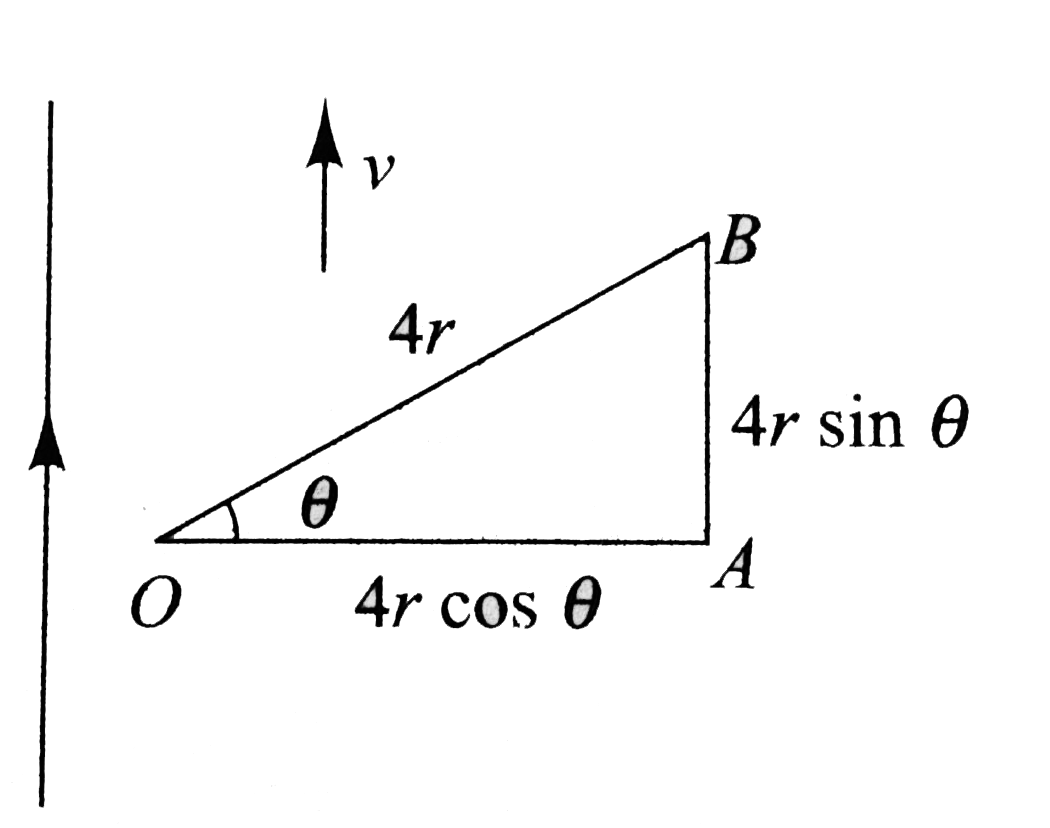
Join the end points O and b and replace the two semicircles bya straight rod of length 4r (Fig. 3.57).
Induced emf in straight rod OB will be same as in the actual conductor. Now this straight rod can be replaced by a combination of two rods OA and AB. induced emf in OB will be same as the sum of induced emf in OA and induced emf in AB. But induced emf in AB will be zero because its velocity will be parallel to its length. Hence, induced emf in OA will be the net induced emf in actual conductor.
We now have a ros of effective length 4rcosθ translating in a non-uniform magnetic field. consider a small element of the wire of length dx located at a distance x from the wire. The magnetic field at this element is B=(μ)(0)I2πx ltbr> The potential difference across this element is dV=μ0I2πxvdx.
The potential difference across the ends of the rod can be calculated by integrating over the whole end. Therefore,
V=∫dV=∫d−2rcosθd+2rcosθμ0I2πxvdx
=μ0Iv2π1n[d+2rcosθd−2rcosθ]
From the right hand rule, we see that electrons will accumulate at end B. Therefore, end O is at a higher potential than B.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Solved Example
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.1
15 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
Figure shows an irregular shaped wire AB moving with velocity v, as shown. Find the emf induced in the wire
View SolutionThe current carrying wire and the rod AB are in the same plane. The rod moves parallel to the wire with a velocity v . Which one of the following statements is true about induced emf in the rod
View SolutionA straight wire carrying current is parallel to the y-axis as shown in Fig. The
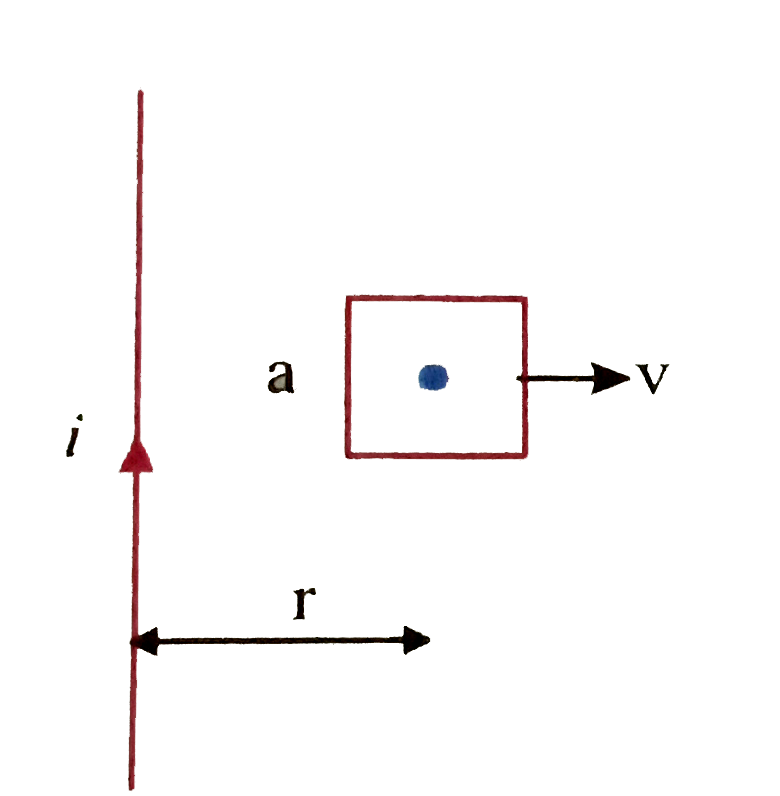
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
View SolutionA long wire carrying a steady current I lies in the plane of circular conducting loop placed at a certain distance from the wire. There will be an induced current in the loop if it is
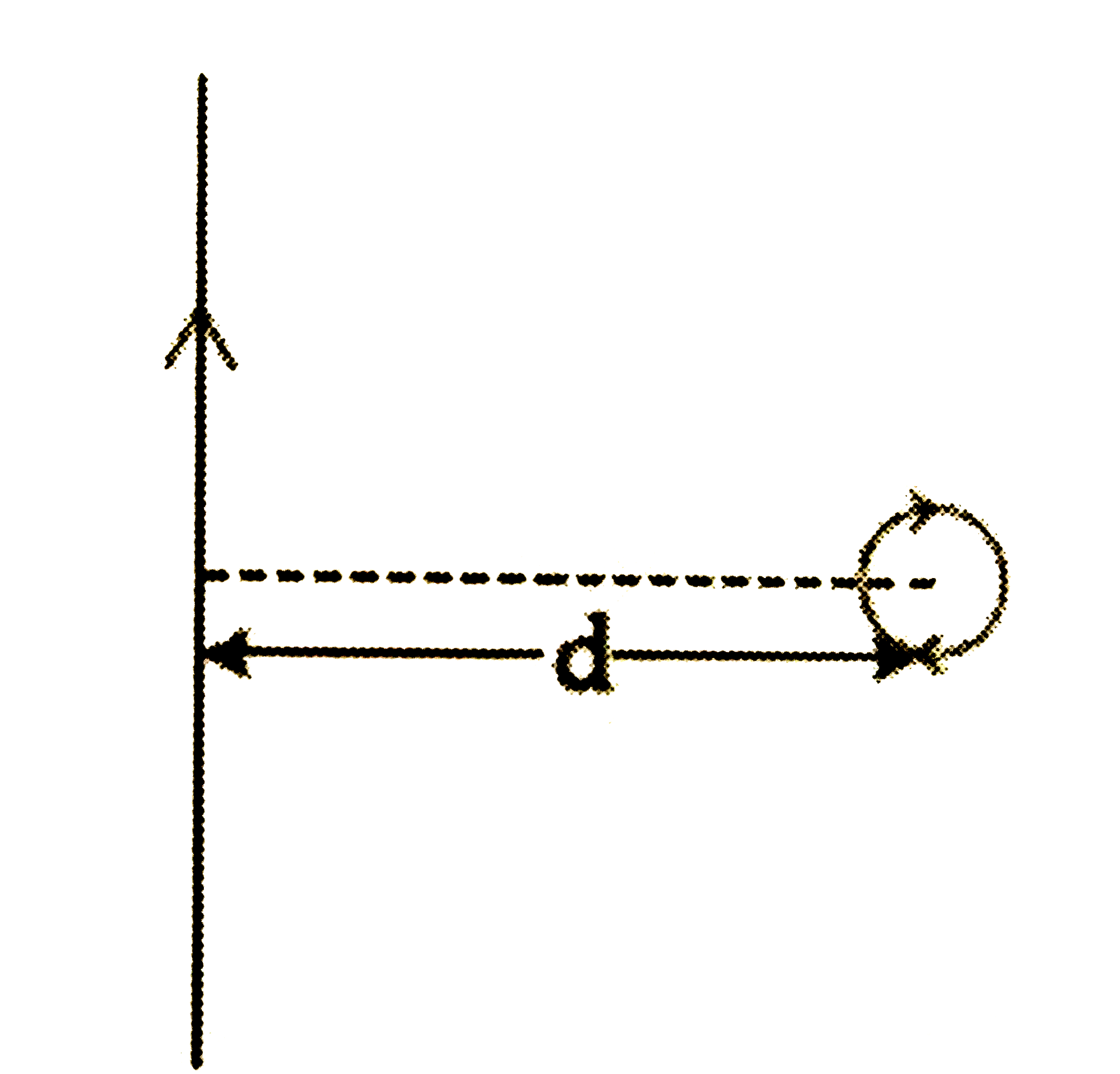
View SolutionAn infinitely long current carrying wire and a small current carrying loop are in the plane of the paper as shown. The radius of the loop is a and distance of its centre from the wire is d (d>>a). If the loop applies a force F on the wire then :
View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View SolutionAn infinitely long current carrying wire and a small current carrying loop are in the plane of the paper as shown. The radius of the loop is a and distance of its centre from the wire is d (d>>a). If the loop applies a force F on the wire then :

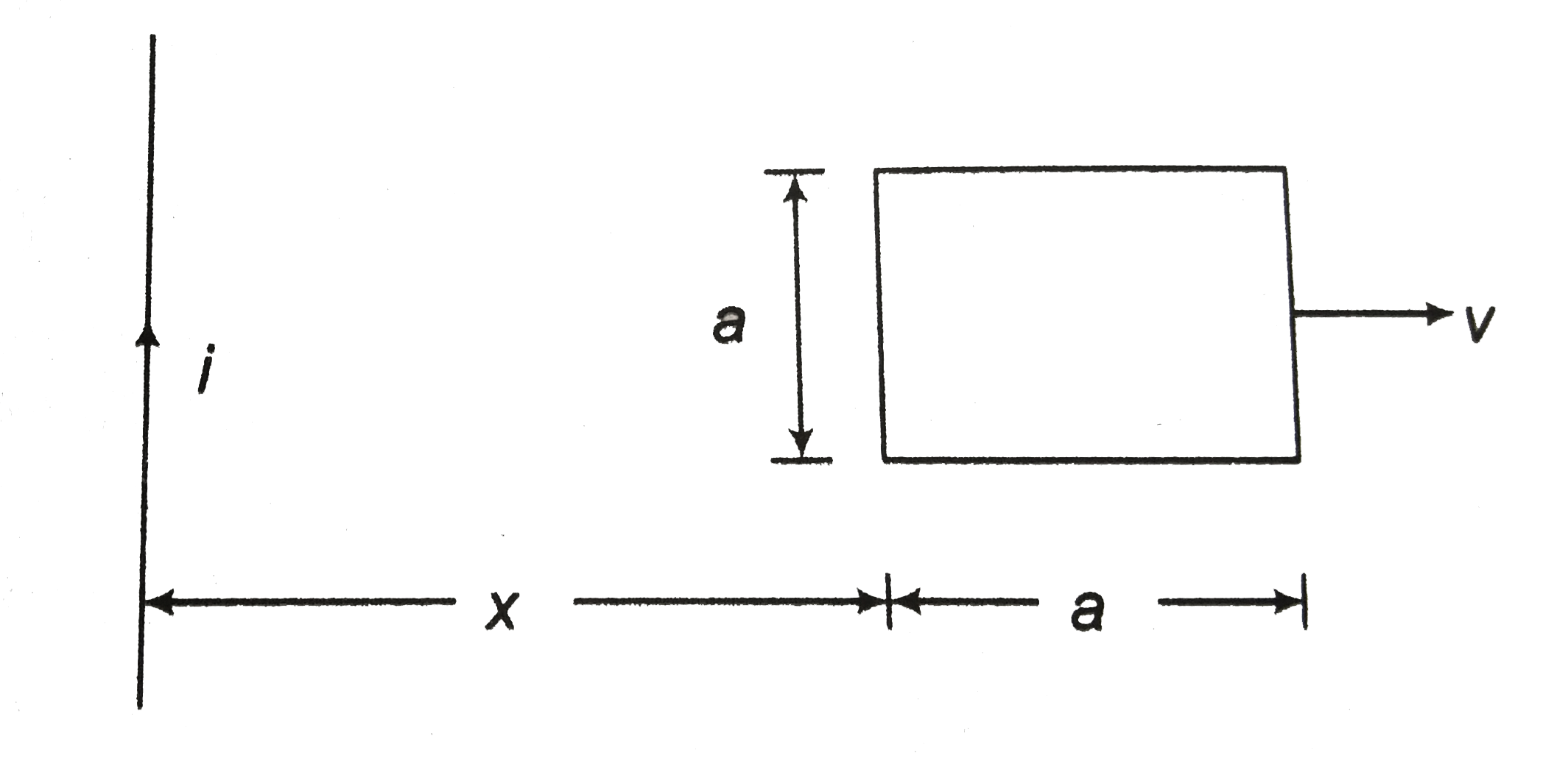
View SolutionA square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
View Solution