A long solenoid with radius 2cm carries a current of 2A. The solenoid is 70cm long and is composed of 300 turns of wire. Assuming ideal solenoid model, calculate the flux linked with a circular surface if
(a) it has a radius of 1cm and is perpendicular to the axis of the solenoid:
(i) inside,
(ii) outside.
(b)it has a radius of 3cm and is perpendicular to the axis of the solenoid with its center lying on the axis of the solenoid.
( c ) it has a radius greater than 2cm and axis of the solenoid subtend an angle of 60∘ with the normal to the area (the center of the circular surface being on the axis of the solenoid).
(d) the plane of the circular area is parallel to the axis of the solenoid.
To solve the problem step by step, we will calculate the magnetic flux linked with a circular surface in different scenarios as described in the question.
Given Data:
- Radius of the solenoid, Rs=2cm=0.02m
- Current through the solenoid, I=2A
- Length of the solenoid, L=70cm=0.7m
- Number of turns, N=300
Step 1: Calculate the number of turns per unit length n
n=NL=3000.7≈428.57turns/m
Step 2: Calculate the magnetic field inside the solenoid B
Using the formula for the magnetic field inside an ideal solenoid:
B=μ0nI
Where μ0=4π×10−7T m/A.
Calculating B:
B=(4π×10−7)×(428.57)×(2)≈1.076×10−3T
Part (a): Circular surface with radius 1cm
(i) Inside the solenoid
1. Area A of the circular surface:
A=πr2=π(0.01)2=π×10−4m2
2. Calculate the magnetic flux Φ:
Φ=B⋅A⋅cos(0)=B⋅A
Φ=(1.076×10−3)⋅(π×10−4)≈3.38×10−7Wb
(ii) Outside the solenoid
Since the magnetic field outside an ideal solenoid is zero:
Φ=0Wb
Part (b): Circular surface with radius 3cm
1. The area A of the circular surface:
A=π(0.03)2=π×9×10−4m2
2. Calculate the magnetic flux Φ:
Φ=B⋅A⋅cos(0)=B⋅A
Φ=(1.076×10−3)⋅(π×9×10−4)≈3.04×10−6Wb
Part (c): Circular surface with radius greater than 2cm at 60∘
1. The area A remains the same as for 2cm:
A=π(0.02)2=π×4×10−4m2
2. Calculate the magnetic flux Φ:
Φ=B⋅A⋅cos(60∘)=B⋅A⋅12
Φ=(1.076×10−3)⋅(π×4×10−4)⋅12≈6.77×10−7Wb
Part (d): Circular area parallel to the axis of the solenoid
1. The angle θ=90∘:
Φ=B⋅A⋅cos(90∘)=0
Summary of Results:
- (a)(i) Inside: Φ≈3.38×10−7Wb
- (a)(ii) Outside: Φ=0Wb
- (b) Radius 3cm: Φ≈3.04×10−6Wb
- (c) Angle 60∘: Φ≈6.77×10−7Wb
- (d) Parallel: Φ=0Wb
- Radius of the solenoid, Rs=2cm=0.02m
- Current through the solenoid, I=2A
- Length of the solenoid, L=70cm=0.7m
- Number of turns, N=300
n=NL=3000.7≈428.57turns/m
Using the formula for the magnetic field inside an ideal solenoid:
B=μ0nI
Where μ0=4π×10−7T m/A.
B=(4π×10−7)×(428.57)×(2)≈1.076×10−3T
1. Area A of the circular surface:
A=πr2=π(0.01)2=π×10−4m2
2. Calculate the magnetic flux Φ:
Φ=B⋅A⋅cos(0)=B⋅A
Φ=(1.076×10−3)⋅(π×10−4)≈3.38×10−7Wb
Since the magnetic field outside an ideal solenoid is zero:
Φ=0Wb
A=π(0.03)2=π×9×10−4m2
2. Calculate the magnetic flux Φ:
Φ=B⋅A⋅cos(0)=B⋅A
Φ=(1.076×10−3)⋅(π×9×10−4)≈3.04×10−6Wb
A=π(0.02)2=π×4×10−4m2
2. Calculate the magnetic flux Φ:
Φ=B⋅A⋅cos(60∘)=B⋅A⋅12
Φ=(1.076×10−3)⋅(π×4×10−4)⋅12≈6.77×10−7Wb
Φ=B⋅A⋅cos(90∘)=0
- (a)(i) Inside: Φ≈3.38×10−7Wb
- (a)(ii) Outside: Φ=0Wb
- (b) Radius 3cm: Φ≈3.04×10−6Wb
- (c) Angle 60∘: Φ≈6.77×10−7Wb
- (d) Parallel: Φ=0Wb
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Solved Example
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.1
15 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A long solenoid of radius 4 cm, length 400 cmcarries a current of 3 A. The total number of turns is 100. Assuming ideal solenoid, find the flux passing through a circular surface having centre on axis of solenoid of radius 3 cm and is perpendicular to the axis of solenoid (i) inside and (ii) at the end of solenoid.
View SolutionA long solenoid with 40 turns per cm carries a current of 1 A. The magnetic energy stored per unit volume is..... J m−3.
View Solution
Knowledge Check
A solenoid of length 0.6 m has a radius of 2 cm and is made up of 600 turns If it carries a current of 4 A, then the magnitude of the magnetic field inside the solenoid is
A6.024×10−3TB8.024×10−3TC5.024×10−3TD7.024×10−3TThe torque required to hold a small circular coil of 10 turns, area 1mm2 and carrying a current of (2144)A in the middle of a long solenoid of 103turns/m carrying a current of 2.5A, with its axis perpendicular to the axis of the solenoid is
 A1.5×10−6NmB1.5×10−8NmC1.5×106NmD1.5×108Nm
A1.5×10−6NmB1.5×10−8NmC1.5×106NmD1.5×108Nm
A long solenoid of 50 cm length having 100 turns carries a current of 2.5A. The magnetic field at centre of solenoid is:
View SolutionA thin solenoid of length 0.4m and having 500 turns of wire carries a current 1A,then find the magnetic field on the axis inside the solenoid.
View SolutionA solenoid of length 0.4m and having 500 turns of wire carries a current of 3amp.Calculate the torque requred to hold a coil (having radius 0.02cm current 2A and turns 50)in the middle of the solenoid with its axis perpendicular to the axis of the solenoid.(π2=10)
View SolutionA long thin solenoid has 900tuns/metre and radius 2.50cm,. The current in the solenoid is increasing at a uniform rate of 60A/s. What is the magnitude of the induced electric field at a point?
a. 0.5cm from the axis of the solenoid.
b. 1.0cm from the axis of the solenoid.
View SolutionA solenoid of length 0⋅5m has a radius of 1cm and is made up of 500 turns. It carries a current of 5A. What is the magnitude of the magnetic field inside the solenoid?
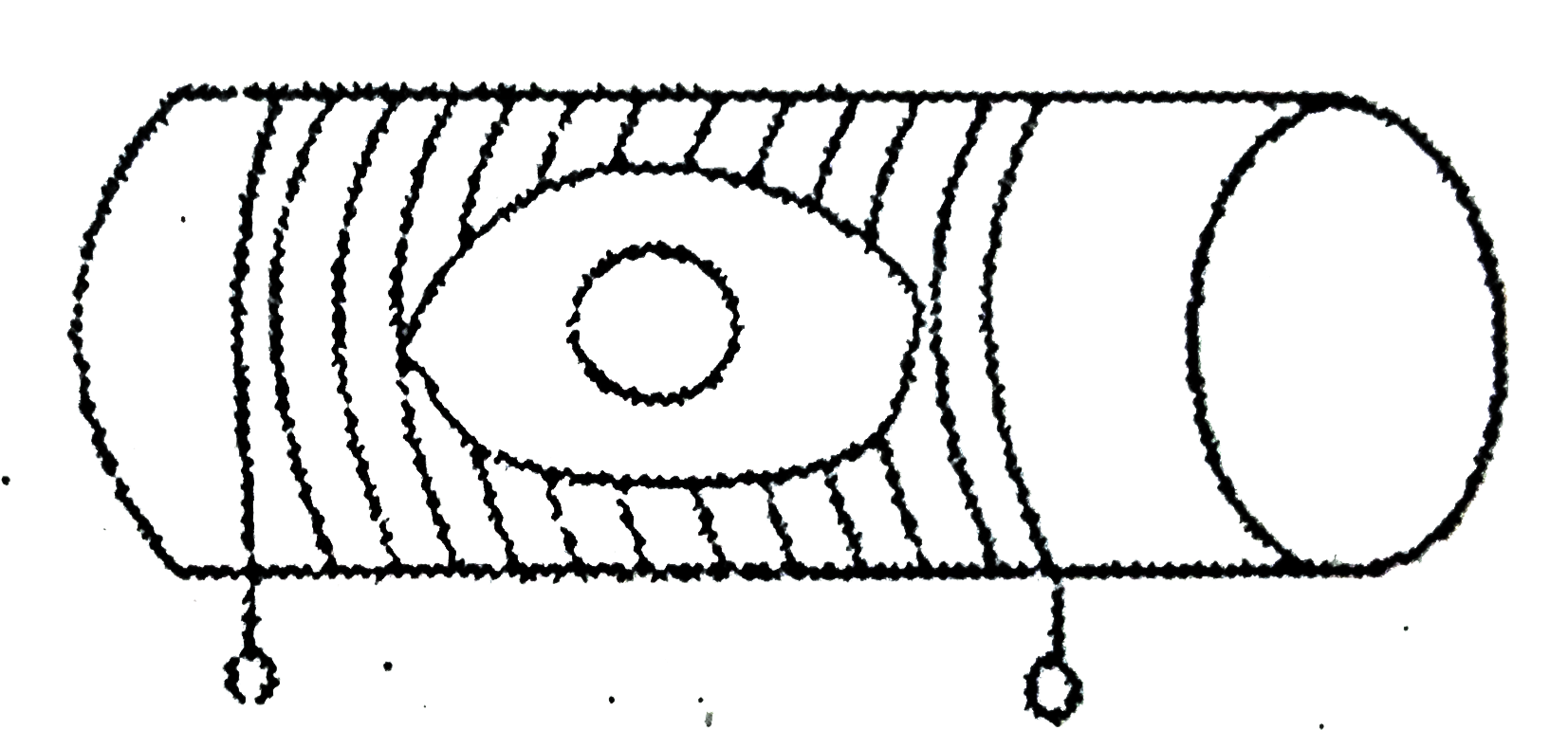
View SolutionA circular coil with a cross-sectional area of 4cm2 has 10 turns. It is placed at the center of a long solenoid that has 15 turns/cm and a cross sectional area of 10cm2, shown in the figure. The axis of the coil conicides with the axis of the solenoid. What is their mutual inductance?
View Solution
