A wire carrying current i has the configuration as shown in figure. Two semi-infinite straight sections, both tangent to the same circle, are connected by a circular arc of central angle theta, along the circumference of the circle, with all sections lying in the same plane. What must be for B to be zero at the centre of the circle?
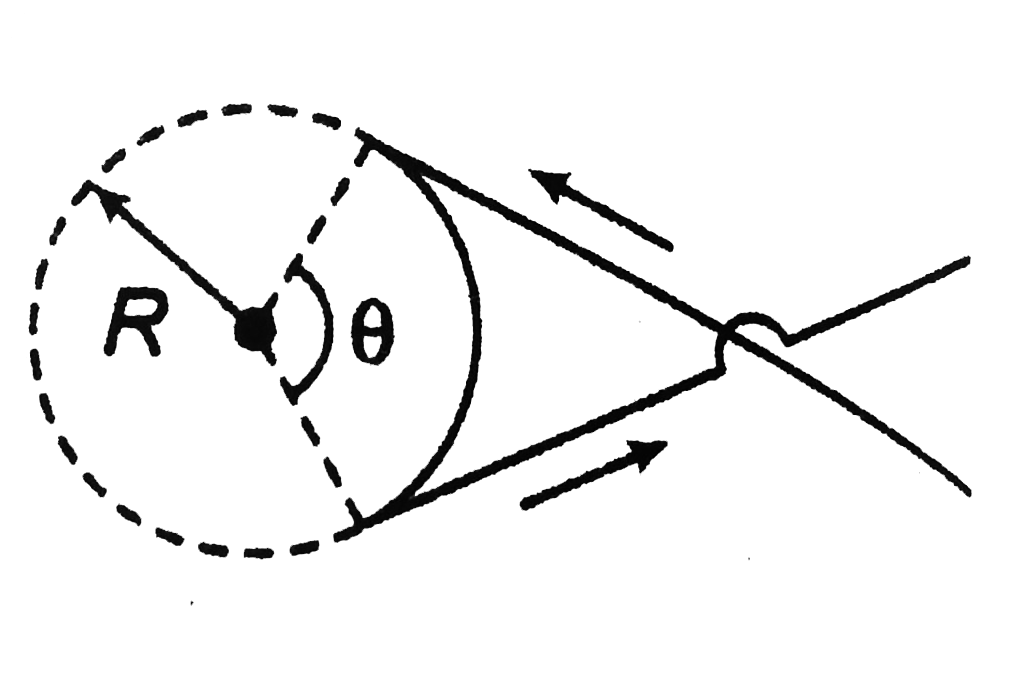
The correct Answer is:(2)
(2) Magnetic field at O due to wire 1 is,
→B1=μ0i4πR⊙
and that due to wire 2 is
→B2=μ0i4πR⊙⇒→B=→B1+→B2=μ0i2πR⊙

Magnetic field at the centre due to circular are subtending angle
θ at the centre is given by
→Barc=μ0i2R(θ2π)⊗
If →Bnet=0⇒→B+→Barc=0
⇒→B=−→Barc
⇒μ0i2πR⊙=−μ0i2R(θ2π)⊗
⇒μ0i2πR=μ0i2R(θ2π)=1π=θ2π⇒θ=2rad
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (fill In The Blanks)
1 Video
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (single Correct Anser)
13 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (linked Comprehension)
21 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
A part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View SolutionTwo very long wires carrying equal current i are bent and arranged as shown in figure. Both AB and CD are arcs of the same circle, both subtending right angles at the centre O. The magnetic field at O is:

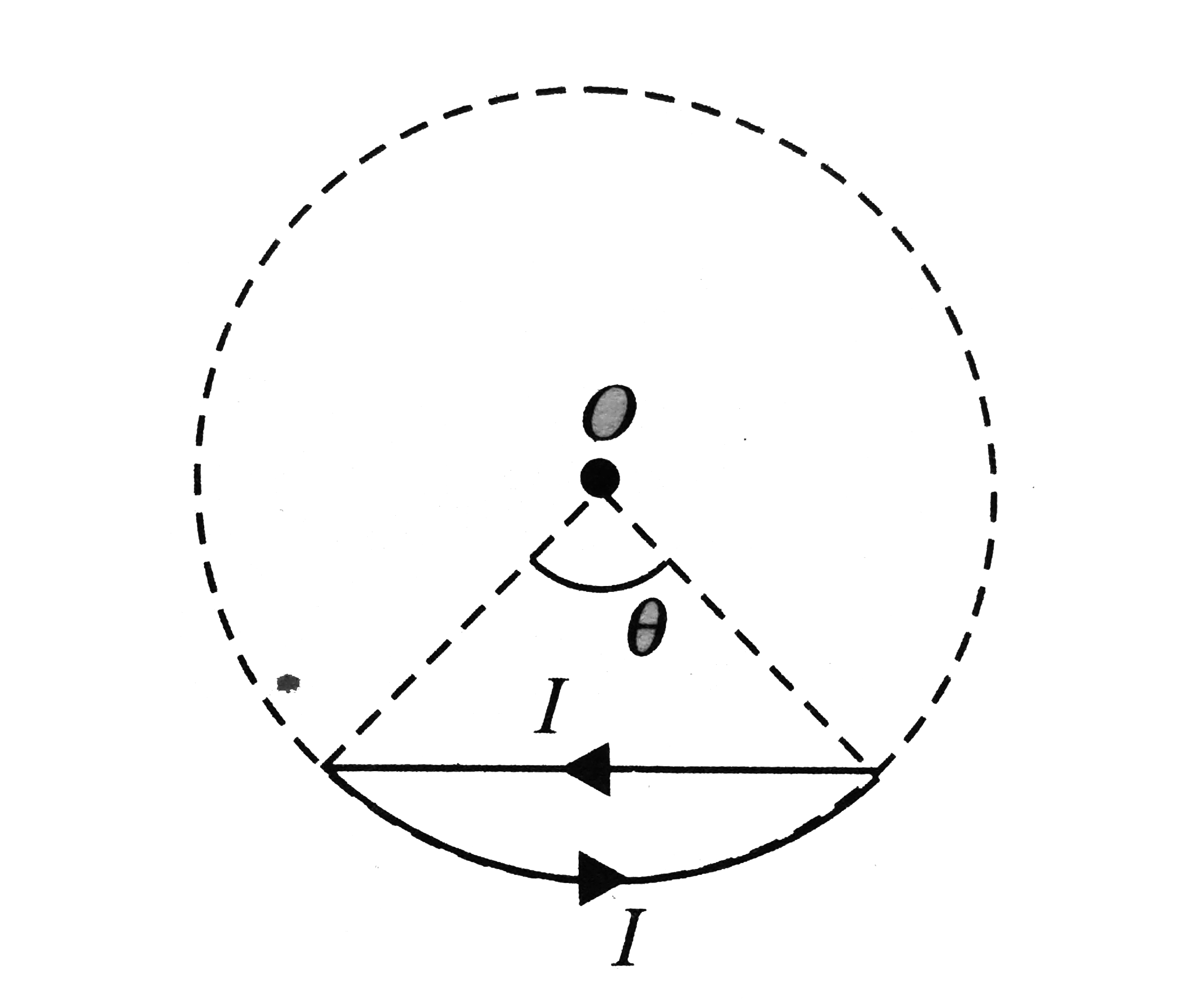
View SolutionFigure. Shows a small loop carrying a current I. The curved portion is an arc of a circle of radius R and the straight portion is a chord to the same circle subtending an angle θ. The magnetic induction at centor O is
View SolutionA conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.

View SolutionA current of 10A flows around a closed path in a circuit which is in the horizontal plane as shown in the figure. The circuit consists oi eight alternating arcs of radii r1=0.08m and r2=0.12m. Each subtends the same angle at the centre.
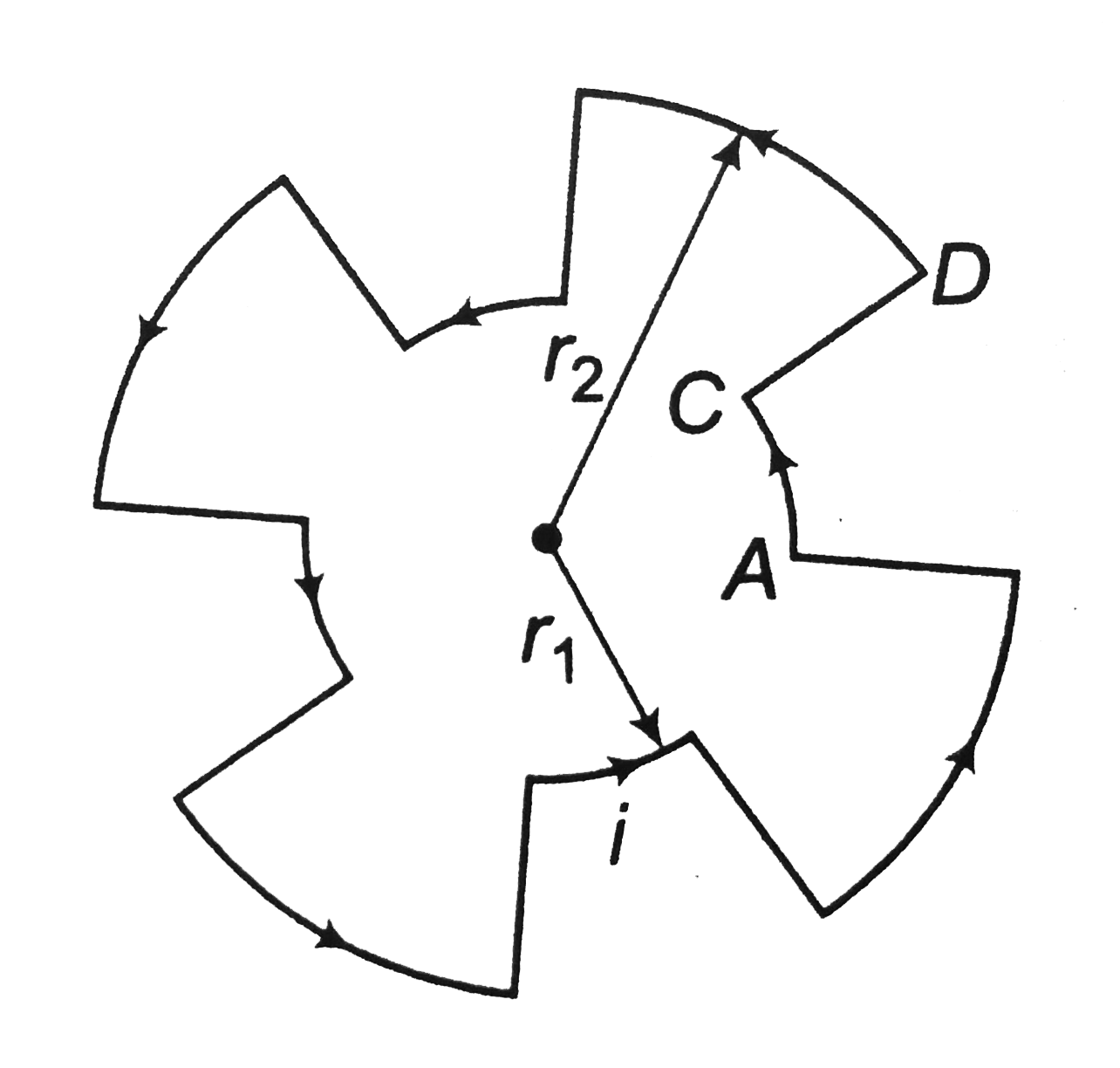
a. Find the magnetic field produced by this circuit at the centre.
b. An infinitely long straight wire carrying as current of 10A is passing through the centre of the above circuit vertically with the direction of the current being into the pane of the circuit. what is the force acting on the wire at the centre due to the current in the circuit? What is the force acting on the arc AC and the straight segment CD due to the current at the centre?
View SolutionA semi circular arc of radius r and a straight wire along the diameter, both are carrying same current i find out magnetic force per unit length on the small element P, which is at the centre of curvature.

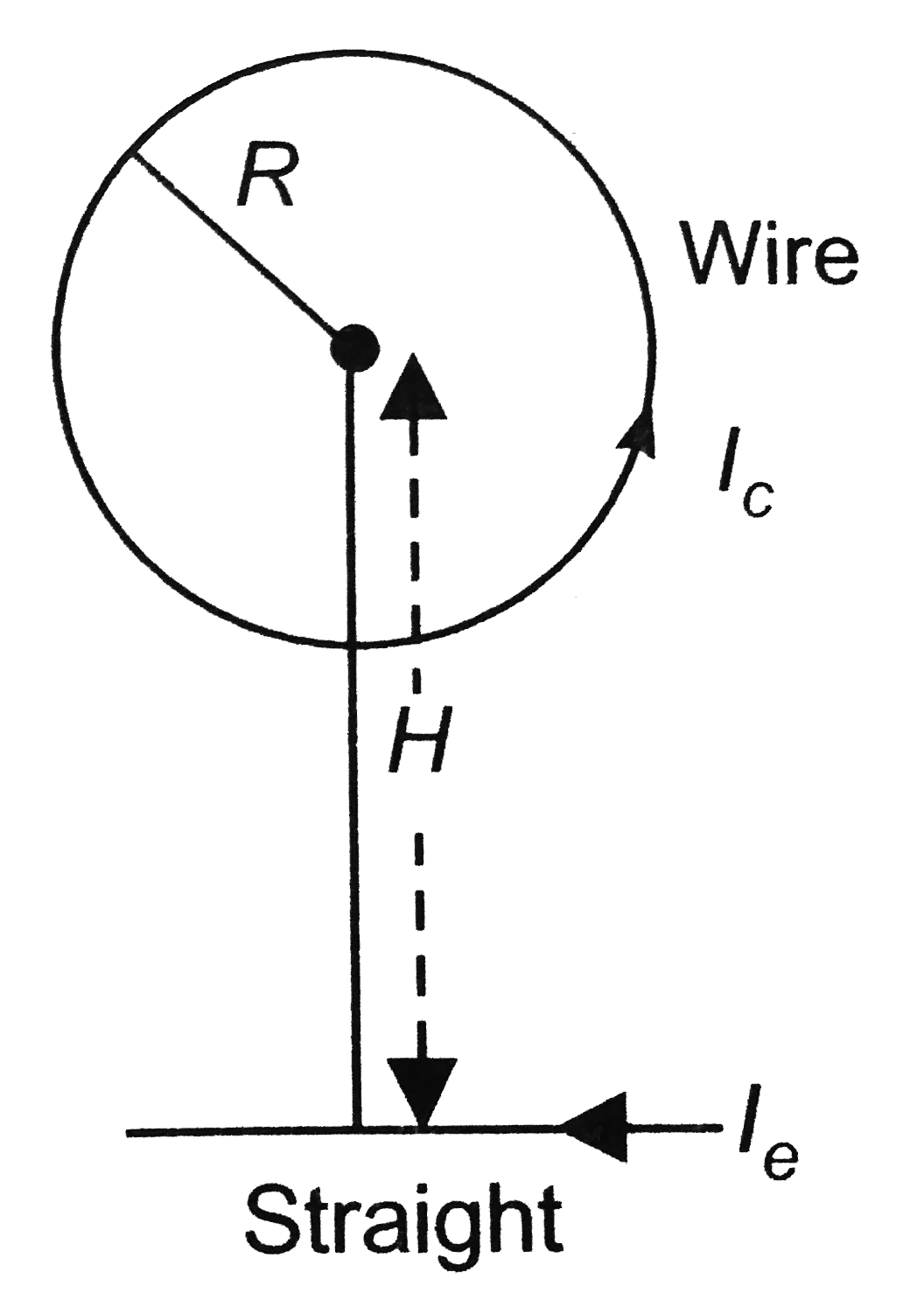
View SolutionCircular loop of a wire and a long straight wire carry current Ic and Ierespectively as shown in figure. Assuming that these are placed in the same plane. The magnetic field will be zero at the centre of the loop when the separation H is:
View SolutionA current I, flowing in a long and straight wire along z-axis, is directed into two identical semicircular portions lying in y-z and x-z planes as shown in the figure. The magnetic field at the centre O is
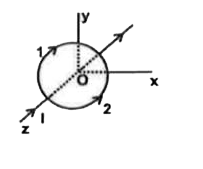
View SolutionFind :
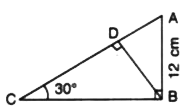
(i) BC
View Solution
