Let BPandBQ be the magnetic field produced by wire P and Q which are placed symmetrically in a rectangular loop ABCD. Current in wire P is directed I inward and in Q is 2I outward.
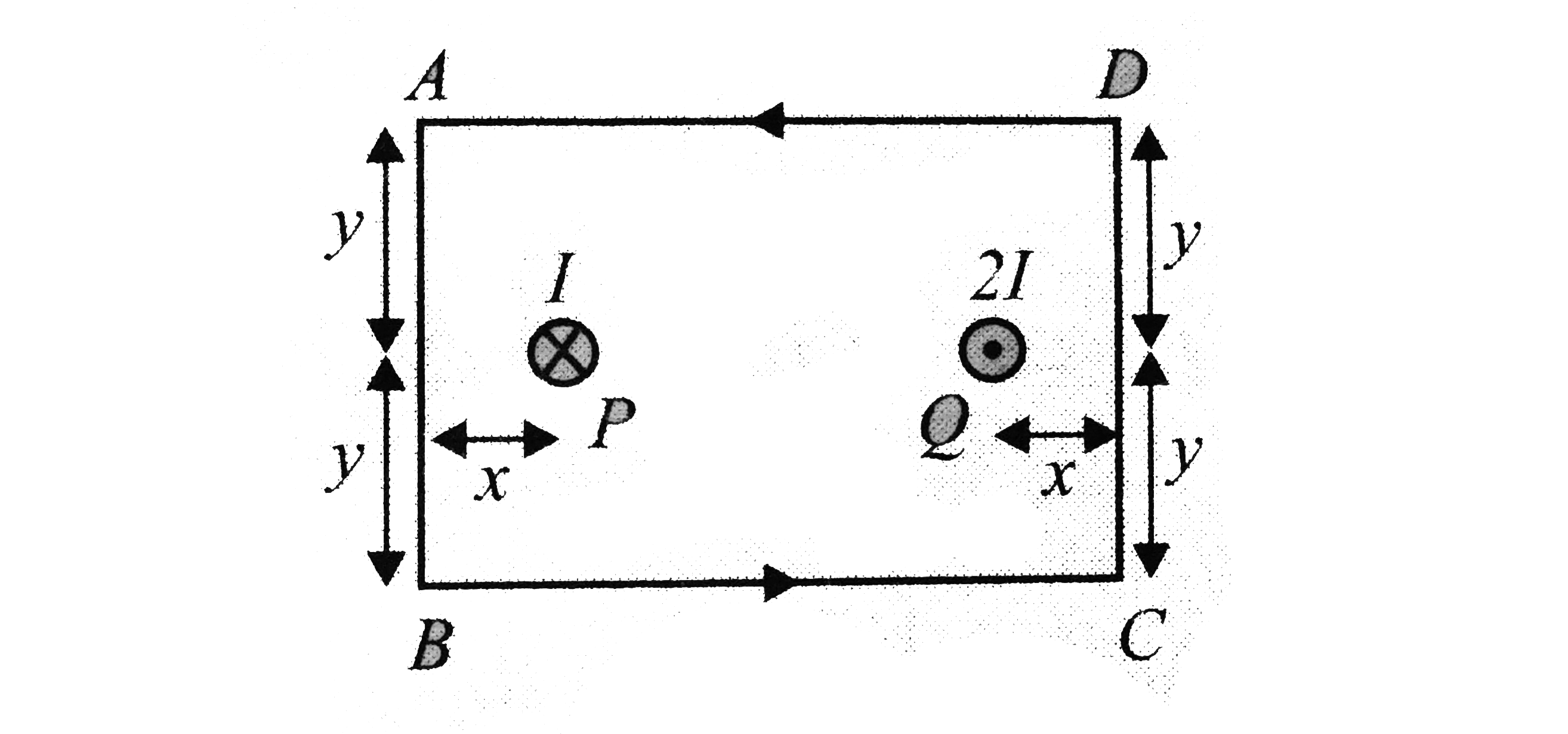
If ∫BA→BQ.d→l=2μ0T−m
∫BD→BP.d→l=−2μ0T−m
∫BA→BP.d→l=−μ0T−m
Then find I.
P→AB,CD,DA,BC
Q→AB,CD,DA,BC
Given ∫BA→BQ.d→l=2μ0T−m
∫BD→BP.d→l=−2μ0T−m
∫BA→BP.d→l=−μ0T−m
we know ∫→Bnet.D→l=μ0(2I−I)=μ0I
Using superpostion taking wire P only
∫→BP.d→l=−μ0Iand∫→BQ.d→l=μ02I
∫BA→BPd→l+∫CB→BPd→l+∫DA→BPd→l+∫AD→BPd→l=−μ0I
From symmetry it is clear ∫CB→BPd→l=∫AD→BPd→l
As ∫BA→BQd→l=2μ0I
Hence, ∫CB→BPd→l=−μ0I
Also, ∫AD→BQd→l=−2μ0I
Then, ∫DA→BQd→l=4μ0I=∫→BQd→l
∫BA→BPd→l=−μ0I⇒∫CD→BQd→l=2μ0I
∫→Bnetd→l=∫→BPd→l+∫→BQd→l=μ0I
=[−μ0I−μ0I−2μ0I−2μ0I]
+[2μ0I+2μ0I+4μ0I+4μ0I]
=−6μ0I+12μ0I=μ0(6I)
Hence, I=6A.
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example
20 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.1
35 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
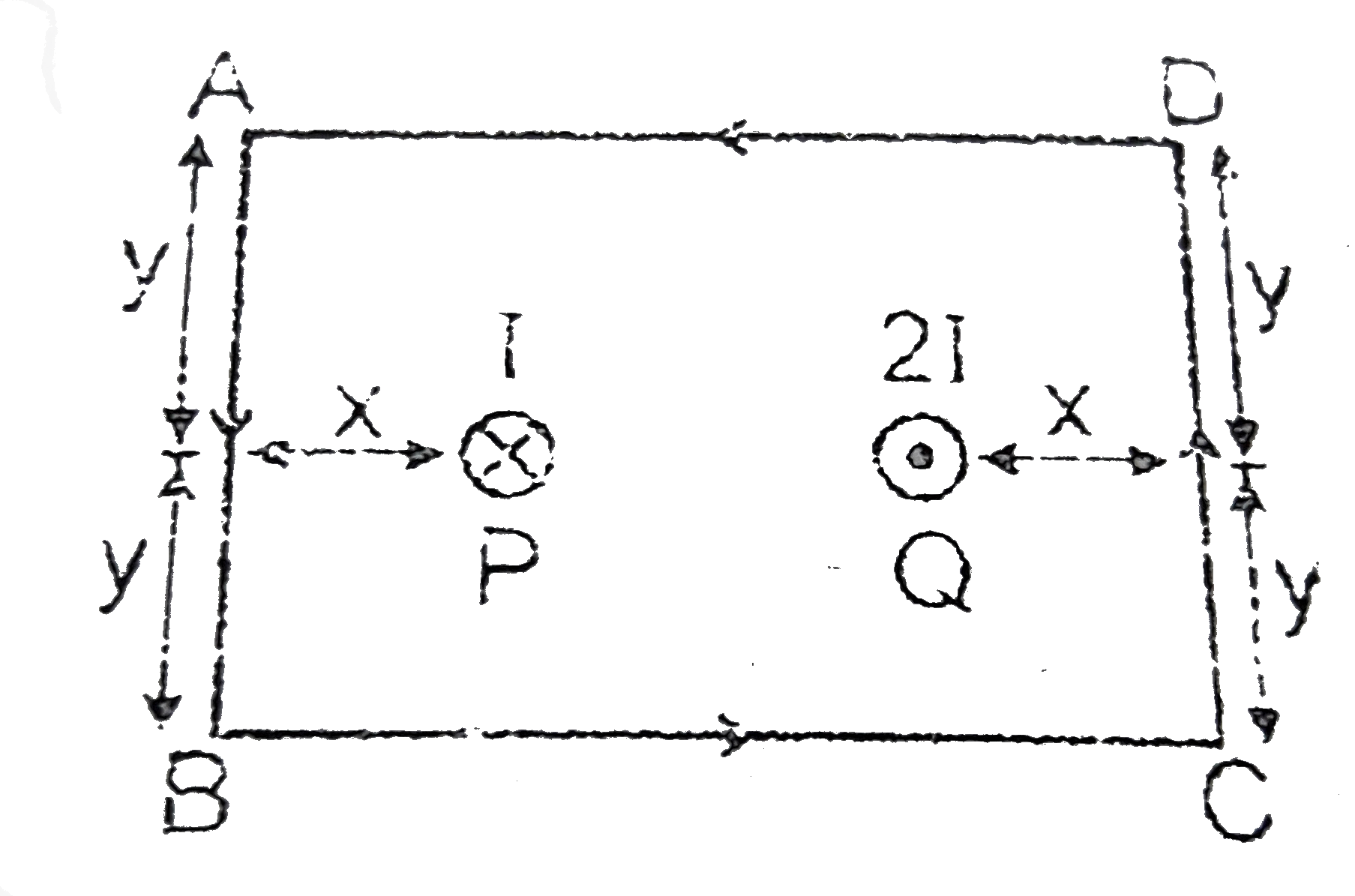
Let BP and BQ be the magnetic field produced by the wire P and Q which are placed symmetrically in a rectangular loop ABCD as shown in figure.Current in wire P is I directed inward and in Q is 2I directed outwards.if ∫BA→BQ.→dl=2μ0 tesla meter,∫AD→BP.→dl=−2μ0 tesla meter,&∫BA→BP.→dl=−μ0 tesla meter tesla meter the value of I will be:
View SolutionIn Fig. Two long wires W1andW2, each carrying current I, are placed parallel to each other and parallel to z-axis. The direction of current in W1is outward and in W2 it is inward. Find →B at p and Q.

View SolutionIn Fig. Two long wires W1andW2, each carrying current I, are placed parallel to each other and parallel to z-axis. The direction of current in W1is outward and in W2 it is inward. Find →B at p and Q.

View SolutionIf →B1,→B2,→B3and→B4 are the magnetic field due to current I1,I2,I3andI4respectively then in ampere circuital law ∮→B.d→l=μ0I, →B is
_PHY_E06_049_Q01.png)
View SolutionFind the dimensions of
a. electric dipole moment p and
b. magnetic dipole moment M.
The defining equations are p=q.dandM=IA,
whre d is distance, A is area, q is charge and I is current.
View Solutionsides QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350 and ∠PQT=1100, find ∠PRQ.
View SolutionA particle of charge -q and mass m enters a uniform magnetic field →B (perpendicular to paper inward) at P with a velocity v0 at an angle α and leaves the field at Q with velocity v at angle β as shown in fig.

View SolutionTP and TQ are tangents to the parabola y2=4ax at PandQ, respectively. If the chord PQ passes through the fixed point (−a,b), then find the locus of T.
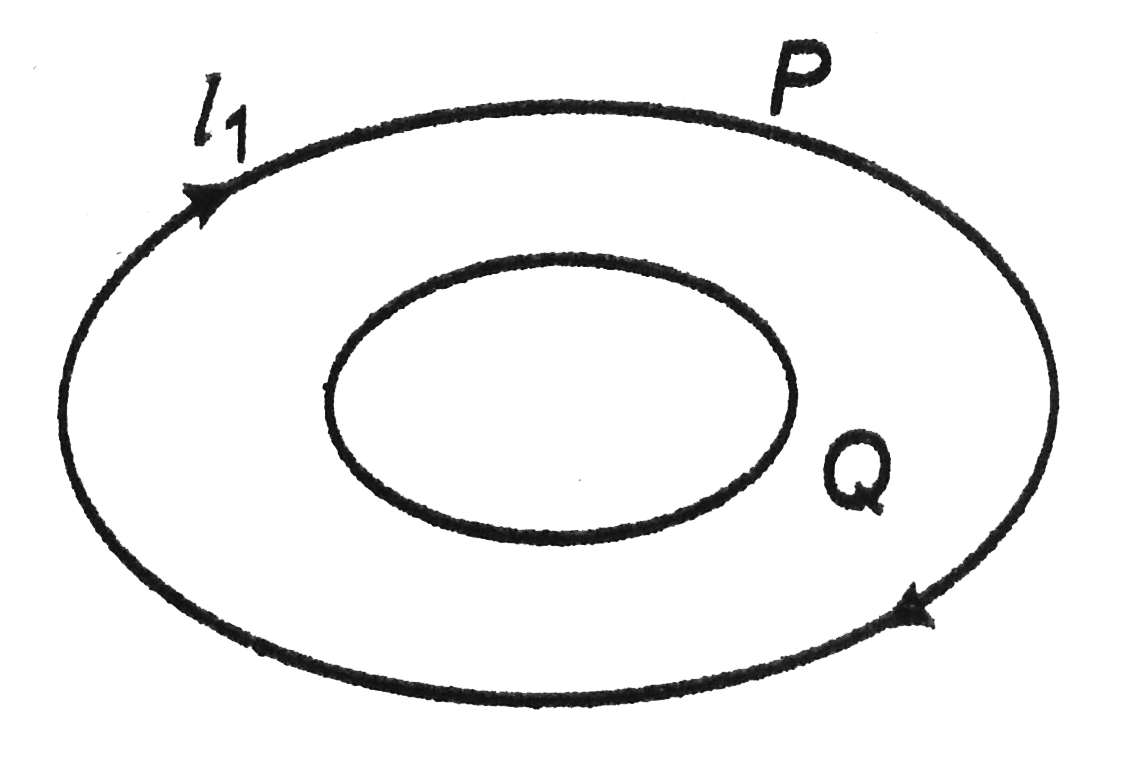
View SolutionTwo circular loops P and Q are concentric and coplanar as shown in figure. The loop Q is smaller than. P. If the current I1 flowing i loop P is decreasing with time, then the curren I2 in the loop Q
View SolutionP and Q are points on sides AB and AC respectively of ABC . If AP=3cm , PB=6cm , AQ=5cm and QC=10cm , show that BC=3 PQ .
View Solution
