A charged particle of mass 10−3kg and charge 10−5C enters a magnetic field of induction 1 T. If g=10ms−2, for what value of velocity will it pass straight through the field without deflection?
10−3ms−1
103ms−1
106ms−1
1ms−1
The correct Answer is:b
To solve the problem, we need to find the velocity at which a charged particle will pass straight through a magnetic field without deflection. This occurs when the magnetic force acting on the particle is equal to the gravitational force acting on it.
1. Identify the Forces Acting on the Particle:
- The gravitational force (F_gravity) acting on the particle is given by:
Fgravity=mg
- The magnetic force (F_magnetic) acting on the particle when it moves through the magnetic field is given by:
Fmagnetic=QvB
where:
- m=10−3kg (mass of the particle)
- g=10m/s2 (acceleration due to gravity)
- Q=10−5C (charge of the particle)
- B=1T (magnetic field induction)
- v is the velocity of the particle.
2. Set the Forces Equal:
For the particle to pass straight through the field without deflection, the magnetic force must equal the gravitational force:
Fgravity=Fmagnetic
Therefore, we have:
mg=QvB
3. Rearrange the Equation to Solve for Velocity (v):
Rearranging the equation gives us:
v=mgQB
4. Substitute the Given Values:
Now, substitute the known values into the equation:
v=(10−3kg)(10m/s2)(10−5C)(1T)
5. Calculate the Velocity:
Performing the calculation:
v=10−2kg m/s210−5C=103m/s
6. Final Answer:
Thus, the velocity at which the charged particle will pass straight through the magnetic field without deflection is:
v=1000m/s
- The gravitational force (F_gravity) acting on the particle is given by:
Fgravity=mg
- The magnetic force (F_magnetic) acting on the particle when it moves through the magnetic field is given by:
Fmagnetic=QvB
where:
- m=10−3kg (mass of the particle)
- g=10m/s2 (acceleration due to gravity)
- Q=10−5C (charge of the particle)
- B=1T (magnetic field induction)
- v is the velocity of the particle.
For the particle to pass straight through the field without deflection, the magnetic force must equal the gravitational force:
Fgravity=Fmagnetic
Therefore, we have:
mg=QvB
Rearranging the equation gives us:
v=mgQB
Now, substitute the known values into the equation:
v=(10−3kg)(10m/s2)(10−5C)(1T)
Performing the calculation:
v=10−2kg m/s210−5C=103m/s
Thus, the velocity at which the charged particle will pass straight through the magnetic field without deflection is:
v=1000m/s
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Exercises Multiple Correct
Explore 25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Exercises Assertion -reasoning
Explore 8 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Exercises Subjective
Explore 10 Videos
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Concept Based
Explore 8 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 3Exercise:True and False
Explore 3 Videos
Similar Questions
A particle of mass 2×10−3 kg, charge 4×10−3C enters in an electric field of 5V/m, then its kinetic energy after 10 s is
View SolutionA particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be
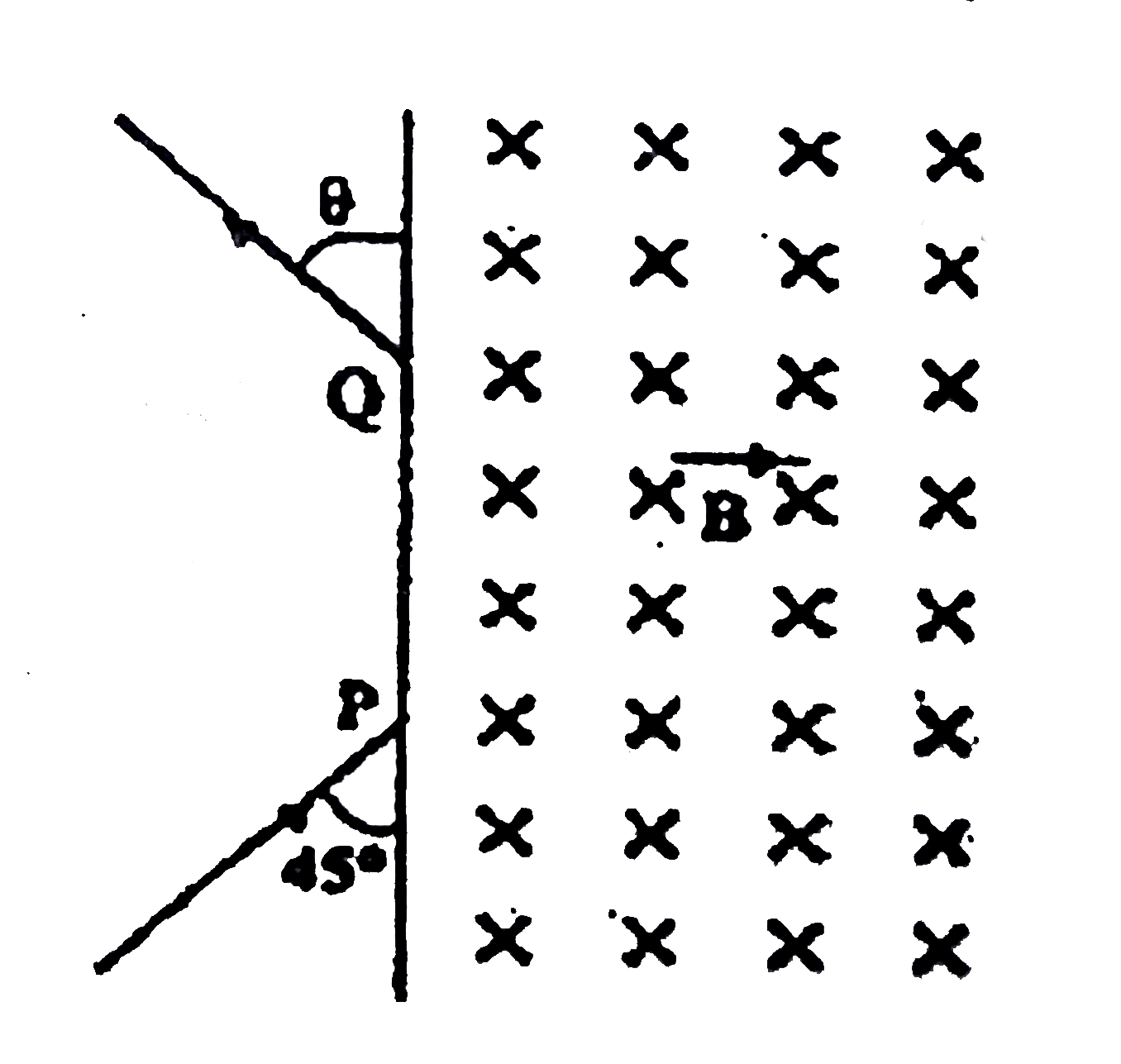
View SolutionA uniform magnetic field of intensity 1T is applied in a circular region of radius 0.1m, directed into the plane of paper. A charged particle of mass 5×10−5kg and charge q=5×10−4C enters the field with velocity 1/√3m/s making an angle of ϕ with a radial line of circular region in such a way that it passes through centre of applied field the angle ϕ is
View SolutionA particle of mass m, charge q and kinetic energy T enters in a transverse uniform magnetic field of induction B. After the 3 s, the kinetic energy of the particle will be
View SolutionA charge particle of mass m and charge q enters in a region of uniform magnetic field as shown in figure.The magnitude of change in linear momentum due to magnetic field will be
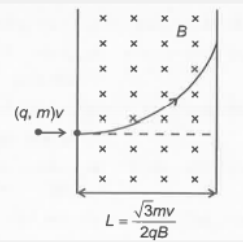
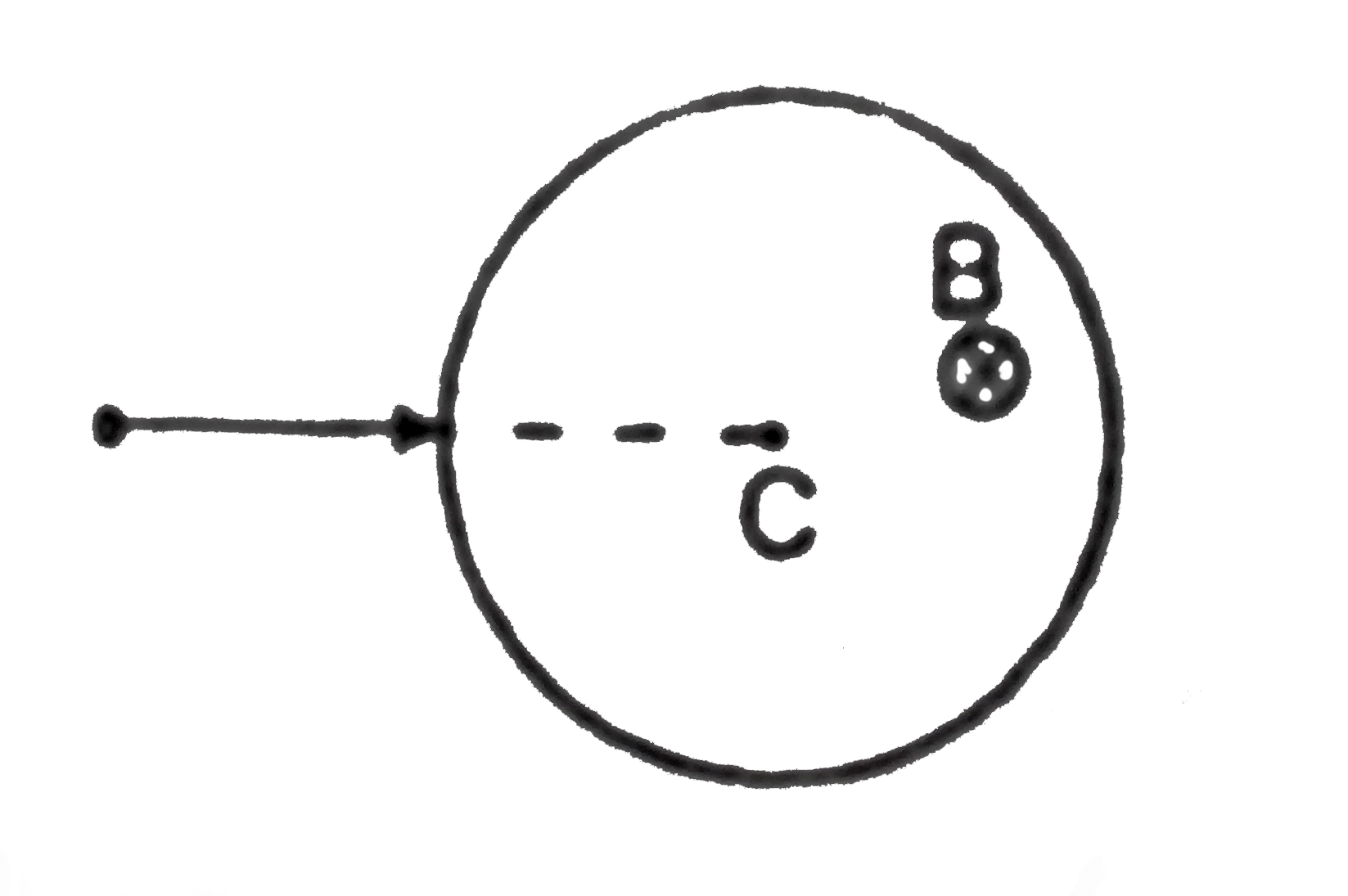
View SolutionIn the figure shown, a charged particle of mass 2 g and charge 5μC enters a circular region of radius 10cm, in which there is a uniform magnetic field of strength 4 T and directed perpendicular to the plane of circular region in the figure. If the particle velocity vector rotates through 90∘ angle in passing through this region then its period is :
View SolutionA proton of mass 1.67×10−27 kg and charge 1.6×10−19C is shot a uniform magnetic field, and perpendicular to the field with a velocity 5×106m/s. If the magnetic induction of the field is 1 tesla, find
(ii) The frequency of revolution.
View SolutionA particle of mass m=1.6X10−27 kg and charge q=1.6X10−19 C moves at a speed of 1.0X107ms−7. It enters a region of uniform magnetic field at a point E, as shown in The field has a strength of 1.0 T. (a) The magnetic field is directed into the plane of the paper. The particle leaves the region of the filed at the point F. Find the distance EF and the angle theta. (b) If the field is coming out of the paper, find the time spent by the particle in the regio the magnetic feld after entering it at E.

View SolutionA charged particle of mass 5×10−5kg is held stationary in space by placing it in an electric field of strength 107NC−1 directed vertically downwards. The charge on the particle is
View SolutionA small particle of mass m = 1 kg and charge of 1C enters perpendicularly in a triangular region of uniform magnetic field of strength 2T as shown in figure :
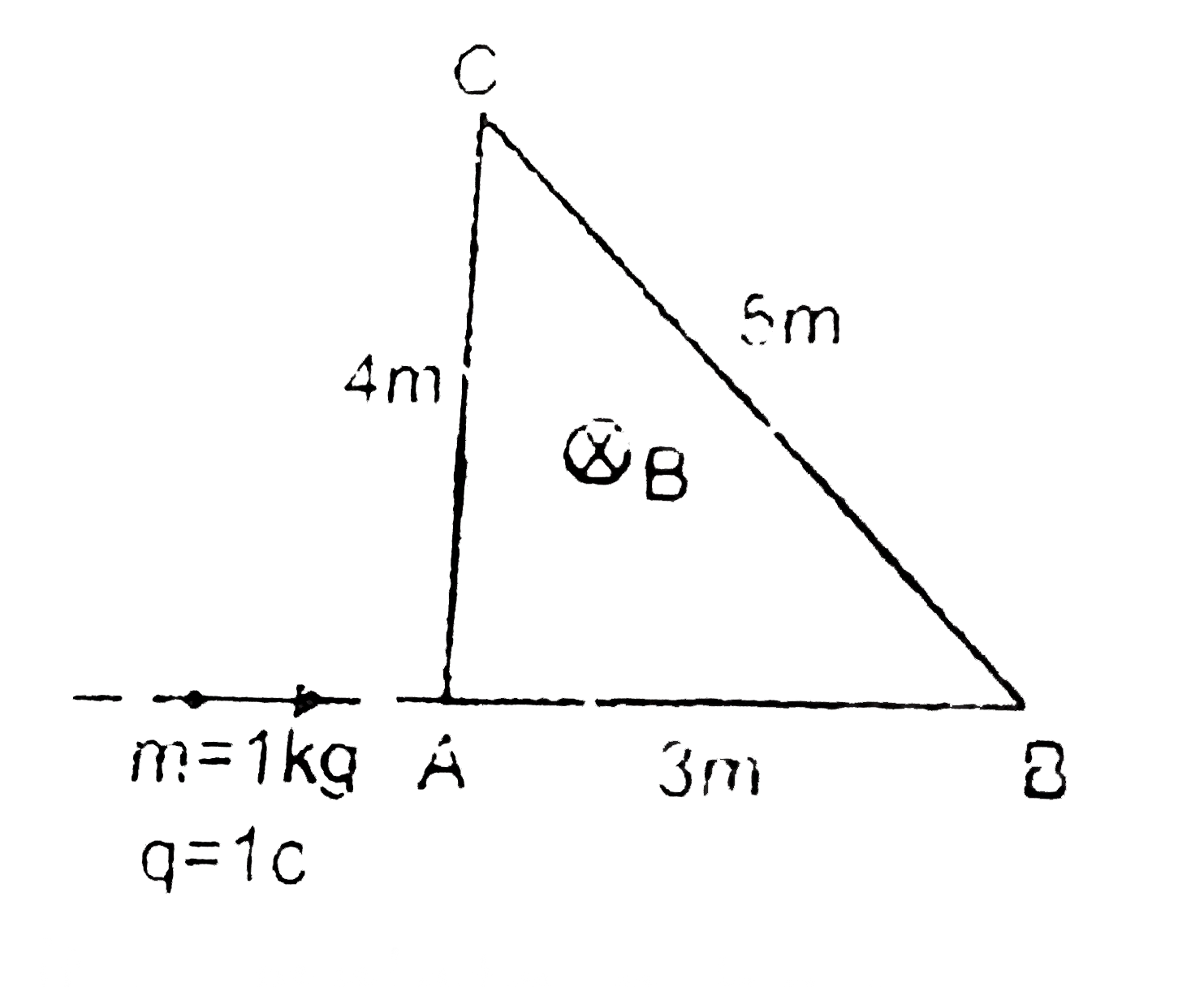
Calculate maximum velocity of the particle with which it should enter so that it complete a half-circle in magnetic region :
View Solution
