Shows two long metal rails placed horizontally and parallel to each other at a separation i. A uniform magnetic field b exists in the vertically downward direction. A wire of mass m can slide on the rails. The rails are connected to a constant current source which drives a current I in the circuirt. The friction coefficient between the rails and the wire is μ. (a) What should be the minimum value of μ which can prevent the wire from sliding on the rails? (b) Describe the motion of the wire if the value of μ is half the value found in the previous part.

(a) The force on the wire due to the magnetic field is
→F=i→l×→BorF=ilb
It acts towards right in the figure provided. If the wire does not
slide on the rails, the force of friction by the rails should be
equal to F. If μ0 be the minimum coefficient of friction which
can prevent sliding, this force is equal to μ0mg. Thus,
μ0mg=ilBorμ0=ilBmg
(b) If the friction coefficient is μ=μ02=ilB2ng, the wire will
slide towards right. The frictional force by the rails is f=μmg=ilB2→wards≤ft
The resultant force is ilB−ilB2=ilB2 towards right. The
accleration will be a=ilB2m. The wire will slide towards
right with this acceleration.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise1.3
14 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Subjective
10 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
Figure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
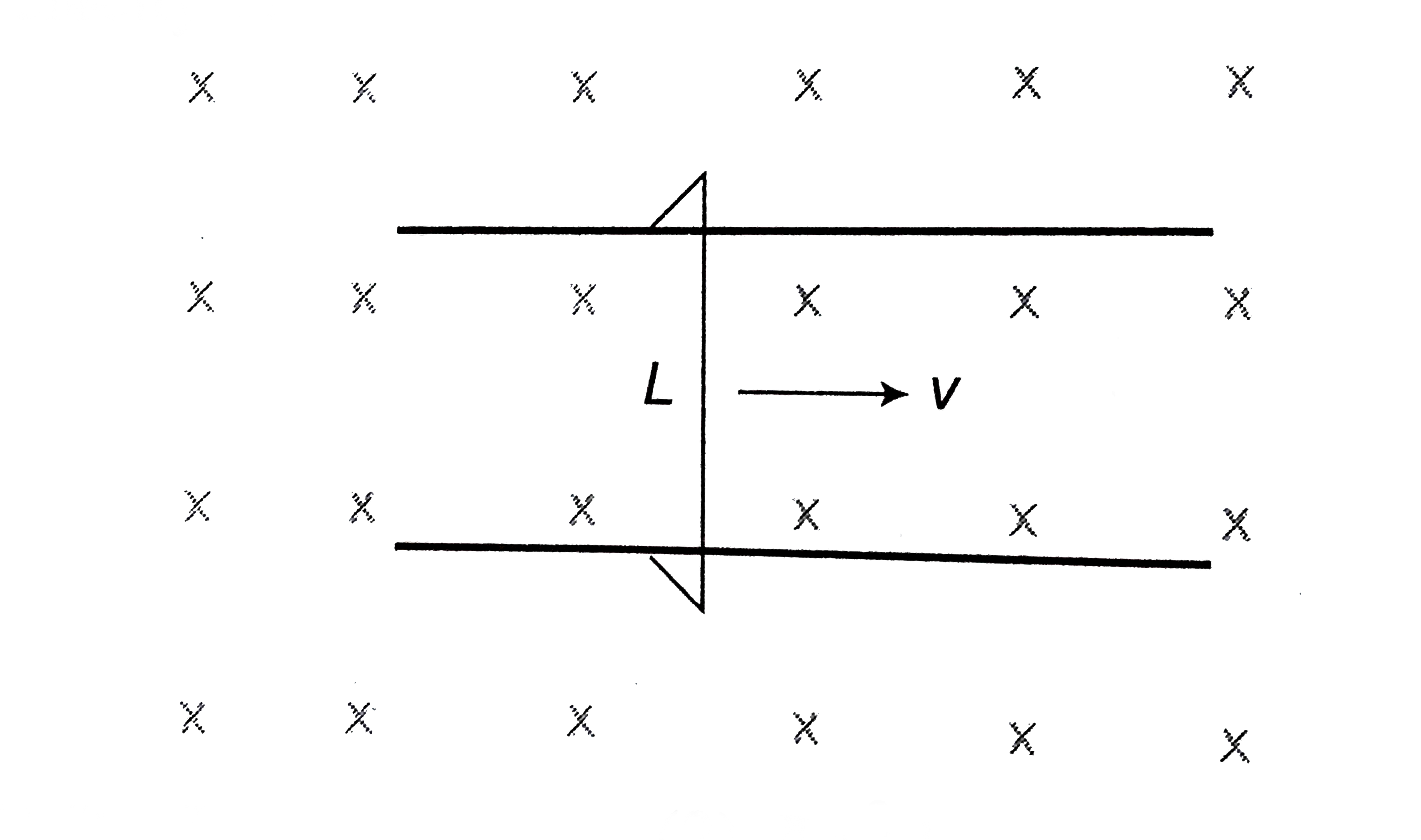
View SolutionShows a wire sliding on two parallel, conducting rails placed at a separaton l. A magnetic feld B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constatn velocity v ?

View SolutionFigure shows a wire of resistance R sliding on two parallel, conducting fixed thick rails placed at a separation l. A magnetic fild B exist in a direction perpendicular to the plane of the rails. The wire is moving with a constant velocity v. Find current through the wire
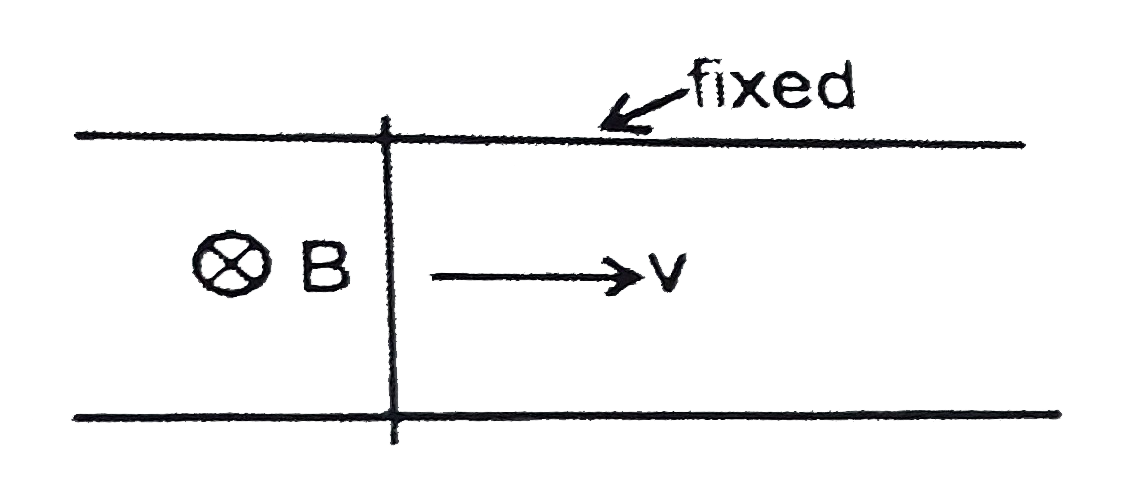
View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionTwo long straight wires are set parallel to each other Each carries a current i in the same direction and the separation between them is 2r. The intensity of the magnetic field midway between them is
View SolutionTwo long straight wires are set parallel to each other. Each carriers a current i in the same direction and the separation between them is 2r. The intensity of the magnetic field midway between them is

View SolutionA wire of mass m and length I can freely slide on a pair of parallel, smooth, horizontal rails placed in a vertical magnetic field B . The rails are connected by a capacitor of capacitance C. The electric resistance of the rails and the wire is zero. If a constant force F acts on the wire as shown in the figure, find the acceleration of the wire.
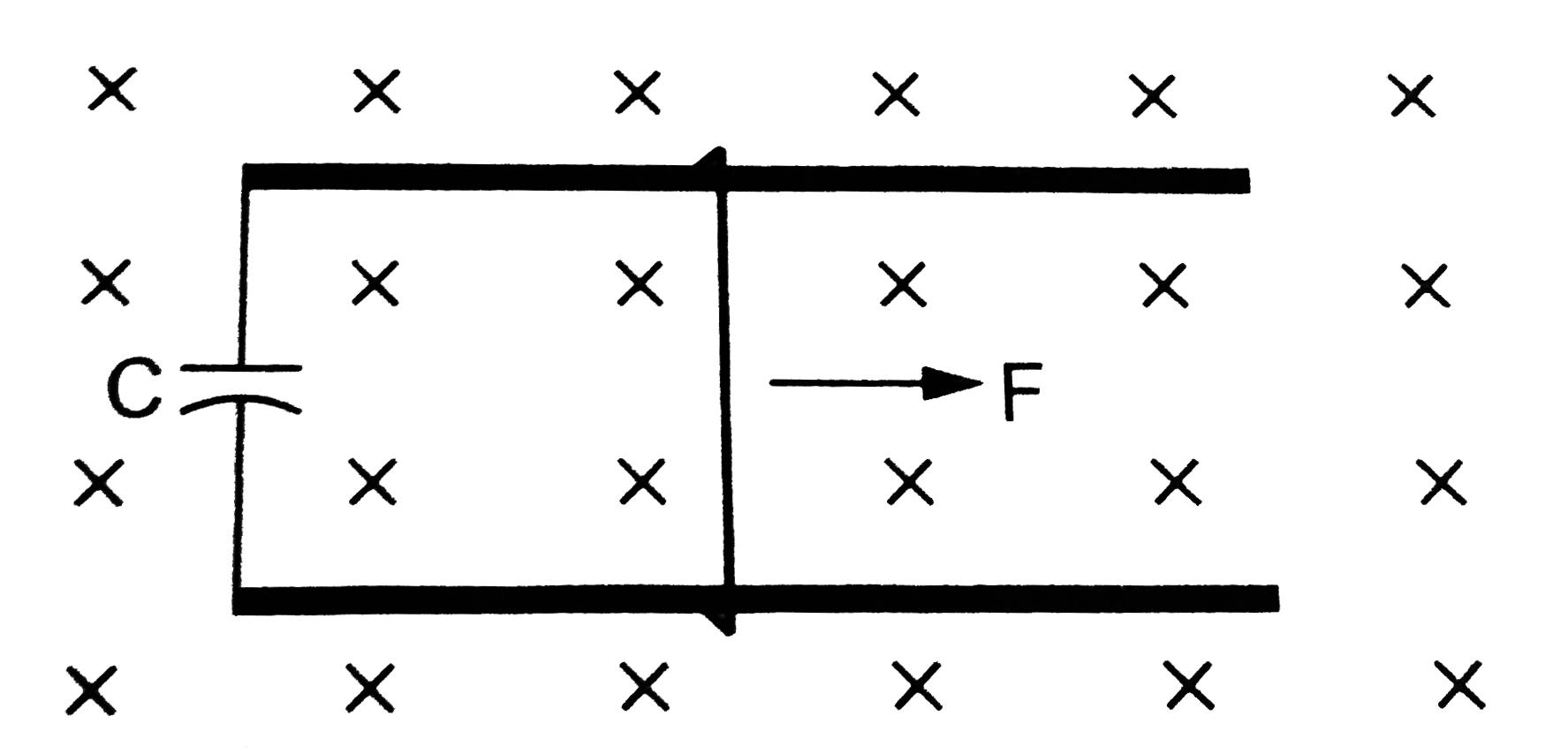
View SolutionA copper rod of mass m rests on two horizontal rails distance L apart and carries a current of I from one rail to the other. The coefficient of static friction between rod and rails is μs What are the (a) magnitude and (b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?
View SolutionTwo long parallel conducting horizontal rails are connected by a conducting wire at one end. A uniform magnetic field B (directed vertically downwards) exists in the region of space.

A light uniform ring of diameter d which is practically equal to separation between the rails is placed over the rails as shown in Fig. If resistance of ring be (λ) per unit length
The current in the wire MN is
View SolutionTwo long parallel conducting horizontal rails are connected by a conducting wire at one end. A uniform magnetic field B (directed vertically downwards) exists in the region of space.

A light uniform ring of diameter d which is practically equal to separation between the rails is placed over the rails as shown in Fig. If resistance of ring be (λ) per unit length
The force required to pull the ring with uniform velocity v is
View Solution
