A mass spectrometer separates ions according to their ratio of charge to mass. Such devices are widely used in silence and engineering to analyze unknown mixtures and to separate isotopes of chemical elements. Figure 1.24 shows ions of charge q and mass m first being accelerated from rest through a potential difference V and then entering a region of uniform magnetic field B pointing out of the page. Only the magnetic force acts on the ions in this region, so they undergo circular motion and, after half an orbit, land on a detector. Find an expression for the horizontal distancexxfrom the entrance slit to the point where an ion lands on the detector.
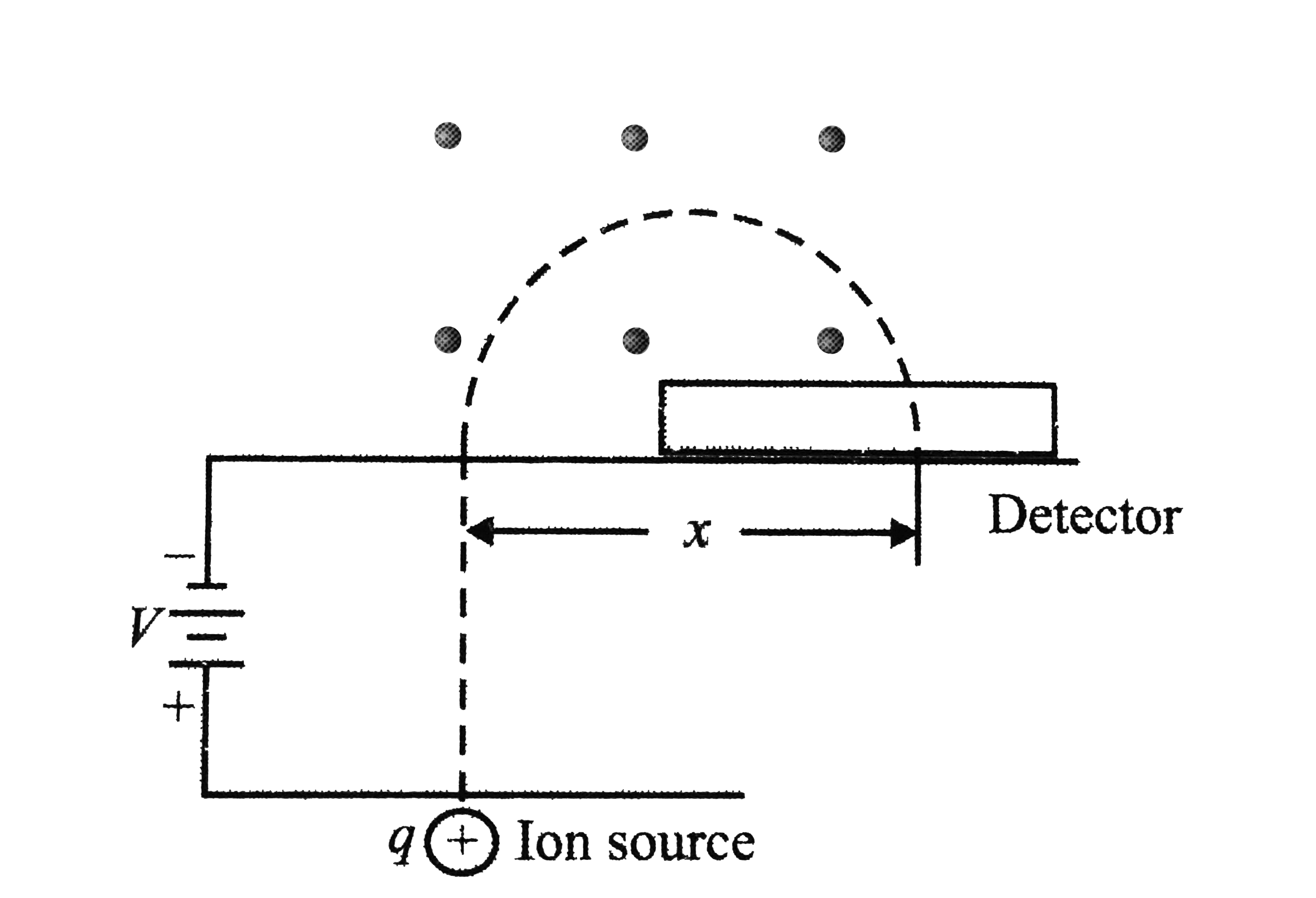
This problem is about charged particle undergoing circular motion in a uniform magnetic field. The distance we are asked for is the diameter of the particle's circular path.
Equation, r=mv/qB, shows that the path radius depends on the field and on the particle's mass, change and speed. We know everything but the speed, so this becomes a two-step problem in which we will first find the speed, We are given the potential difference -energy per unit charge-so we can use energy conservation to find the kinetic energy and hence the ion's speed in the magnetic field region, Then we will use equation to find the radius of the ion's circular path.
A charge q gains kinetic energy qV in ''faling'' through a potential difference V, so an ion's kinetic energy once it enters the magnetic field is
12mv2=qV
Solving for v gives v=√2qV/m.
Our answer, the path diameter x, is then twice the radius gives in equation.
x=2r=2mvqB=2m√2qV/mqB=2B√2mvq.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Solved Example
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
An electron of mass m and charge e is accelerated from rest through a potential difference V in vacuum. The final speed of the electron will be
View SolutionAn electron of mass m and charge e is accelerated from rest through a potential difference V in vacuum. The final speed of the electron will be
View SolutionA particle of charges Q and mass m travels through a potential difference V from rest. The final momentum of the particle is
View SolutionAn electron of mass 'm' is accelerated through a potential difference of V and then it enters a magnetic field of inductionB. Normal to the lines of force. Then the radius of the circular path is
View SolutionThe mass of an electron is m, charge is e and it is accelerated form rest through a potential difference of V volts. The velocity acquired by electron will be :
View SolutionAn electron of mass m and charge e is accelerated by a potential difference V. It then enters a uniform magnetic field B applied perpendicular to its path. The radius of the circular path of the electron is
View SolutionThe mass of an electron is m, its charge is e and it is accelerated from rest through a potential difference, V. The velocity of electron can be calculated by formula:
View SolutionA particle of mass m carrying charge q is accelerated by a potential difference V. It enters perpendicularly in a region of uniform magnetic field B and executes circular arc of radius R, then qm equals
View SolutionA charged particle of mass m and charge q is accelerated through a potential difference of V volts. It enters a region of uniform magnetic field which is directed perpendicular to the direction of motion of the particle. Find the radius of circular path moved by the particle in magnetic field.
View SolutionA charged particle of mass m and charge q is accelerated through a potential differences of V volts. It enters of uniform magnetic field B which is directed perpendicular to the direction of motion of the particle. The particle will move on a circular path of radius
View Solution
