The magnetic field is confirmed in a square region. A positive charged particle of charge q and mass m the limiting velocities of the particles so that it may come out of face (1), (2), (3), and (4). 
For the positive charge coming out from face (1), the radius of the path in magnetic field should be less than or equal to l/4, For limiting case
rmax=l4=mvqB⇒vmax=qBl4m
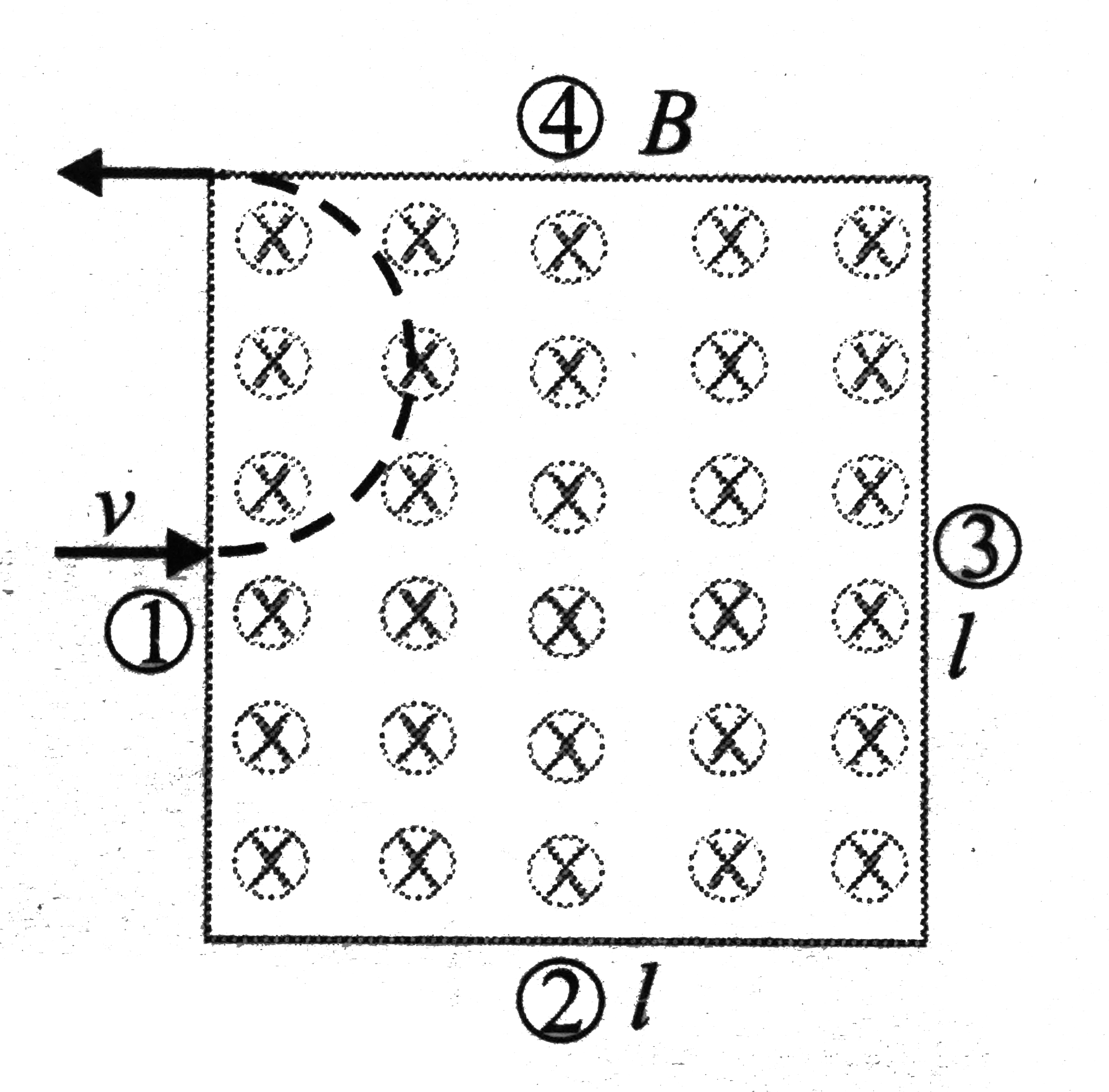
Hence, if the velocity is <qBl4m, the charge particle comes out of face (1).
We can observe for right palm rule that the particle cannot come out from face(1).
For a positive charge comming out of face (4), let particle come out at pont N from
ΔOMN
(OM2)=(ON2)+(MN2)
r2=(r−1.2)2+l2⇒r=54l

If the particle comes out from face (4), r<54limpliesmvqB<54l
or v<54qBlm. If velocity v>54qBlm, the particle will come out from face(3).
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Solved Example
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A positively charged particle projected towards east is deflected towards north by a magnetic field. The field may be
View SolutionA positive charge particle having change q and mass m has velocity →v=v(ˆi+ˆk√2) in the magnetic field B at the origin . Its speed as the function of y is :
View SolutionA charged particle of charge q and mass m enters perpendiculalry in a magnetic field B. Kinetic energy of particle is E, then frequency of rotation is
View SolutionThe magnetic force acting on a charged particle of charge −2μC in a magnetic field of 2T acting y direction, when the particle velocity is (2i+3ˆj)×106ms−1, is
View SolutionSometimes positive charged particle comes from space towards earth with high velocity. Its deviation due to the magnetic field of earth will be:
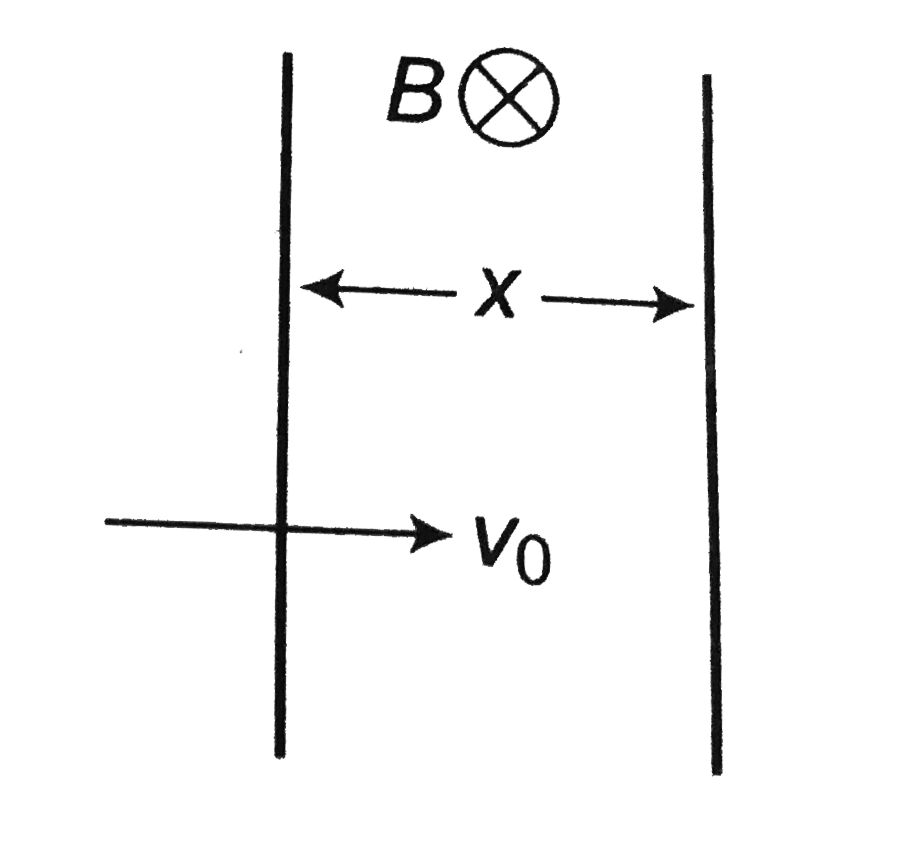
View SolutionA charged particle enters into a uniform magnetic field with velocity v0 perpendicular to it , the length of magnetic field is x=√32R, where R is the radius of the circular path of the particle in the field .The magnitude of charge in velocity of the particle when it comes out of the field is
View SolutionIf a charged particle of charge to mass ratio (qm)=α centers in a magnetic field of strength B at a speed v=(2αd)(B), then

View SolutionIn the figure shown a positively charged particle of charge q and mass m enters into a uniform magnetic field of strength B as shown in the figure.The magnetic field points inwards and is present only within a region of width d.The initial velocity of the particle is perpendicular to the magnetic field and ϕ=30∘.Find the time spent by the particle inside the magnetic field if d=0.2m,B=1T,q=1C,m=1kg and v=1m/s.Use sin45∘=0.7 if required .

View Solutionthe figure shows the path of A positively charged particle through a rectangular region of uniform electric field as shown in the figure. the direction of deflection of particle 2, 3 and 4 is

View SolutionA charged particle enters a uniform magnetic field with velocity v0=4m/s perpendicular to it, the length of magnetic field is x=(√32)R, where R is the radius of the circular path of the particle in the field. Find the magnitude of charge in velocity (in m/s) of the particle when it comes out of the field.
View Solution
