A neutron of energy 1 MeV and mass 1.6×10−27 kg passes a proton at such a distance that the angular momentum of the neutron relative to the proton approximately equals 10−33Js. The distance of closest approach neglecting the interaction between particles is
0.44nm
0.44mm
0.44Å
44fm
The correct Answer is:d
To solve the problem, we need to find the distance of closest approach of a neutron with a proton given that the angular momentum of the neutron relative to the proton is 10−33J s.
1. Understanding Angular Momentum:
The angular momentum L of the neutron relative to the proton can be expressed as:
L=MVR
where:
- M is the mass of the neutron,
- V is the velocity of the neutron,
- R is the distance of closest approach.
2. Given Values:
- Mass of neutron M=1.6×10−27kg
- Energy of neutron E=1MeV=1.6×10−13J
- Angular momentum L=10−33J s
3. Relating Energy to Velocity:
The kinetic energy E of the neutron can be expressed in terms of its mass and velocity:
E=12MV2
Rearranging this gives:
V=√2EM
4. Calculating Velocity:
Substituting the values of E and M:
V=√2×1.6×10−131.6×10−27
V=√2×1014=√2×107m/s≈1.41×107m/s
5. Substituting into Angular Momentum Equation:
Now, substituting V back into the angular momentum equation:
L=MVR
Rearranging for R:
R=LMV
6. Calculating Distance of Closest Approach:
Substituting the known values:
R=10−33(1.6×10−27)(1.41×107)
Calculating MV:
MV=1.6×10−27×1.41×107≈2.26×10−20kg m/s
Now substituting this back into the equation for R:
R=10−332.26×10−20≈4.42×10−14m
7. Final Conversion:
Converting R to femtometers:
R≈44.2fm
Final Answer:
The distance of closest approach is approximately 44fm (femtometers).
The angular momentum L of the neutron relative to the proton can be expressed as:
L=MVR
where:
- M is the mass of the neutron,
- V is the velocity of the neutron,
- R is the distance of closest approach.
- Mass of neutron M=1.6×10−27kg
- Energy of neutron E=1MeV=1.6×10−13J
- Angular momentum L=10−33J s
The kinetic energy E of the neutron can be expressed in terms of its mass and velocity:
E=12MV2
Rearranging this gives:
V=√2EM
Substituting the values of E and M:
V=√2×1.6×10−131.6×10−27
V=√2×1014=√2×107m/s≈1.41×107m/s
Now, substituting V back into the angular momentum equation:
L=MVR
Rearranging for R:
R=LMV
Substituting the known values:
R=10−33(1.6×10−27)(1.41×107)
Calculating MV:
MV=1.6×10−27×1.41×107≈2.26×10−20kg m/s
Now substituting this back into the equation for R:
R=10−332.26×10−20≈4.42×10−14m
Converting R to femtometers:
R≈44.2fm
The distance of closest approach is approximately 44fm (femtometers).
Topper's Solved these Questions
- NUCLEAR PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:NUCLEAR PHYSICSExercise:Linked Comprehension
Explore 29 Videos
- NUCLEAR PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:NUCLEAR PHYSICSExercise:Integer
Explore 6 Videos
- NUCLEAR PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:NUCLEAR PHYSICSExercise:Subjective
Explore 35 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 5Exercise:Integer
Explore 12 Videos
- PHOTOELECTRIC EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:PHOTOELECTRIC EFFECTExercise:Integer Type
Explore 4 Videos
Similar Questions
Knowledge Check
If the earth is a point mass of 6×1024 kg revolving around the sun at a distance of 1.5×108 km and in time T=3.14×107 s, then the angular momentum of the earth around the sun is
A1.2×1018kgm2/sB1.8×1029kgm2/sC1.5×1037kgm2/sD2.7×1040kgm2/s
If the earth is a point mass of 6×1024kg revolving around the sun at a distance of 1.5×108km and in time, T=3.14×107s, then the angular momentum of the earth around the sun is
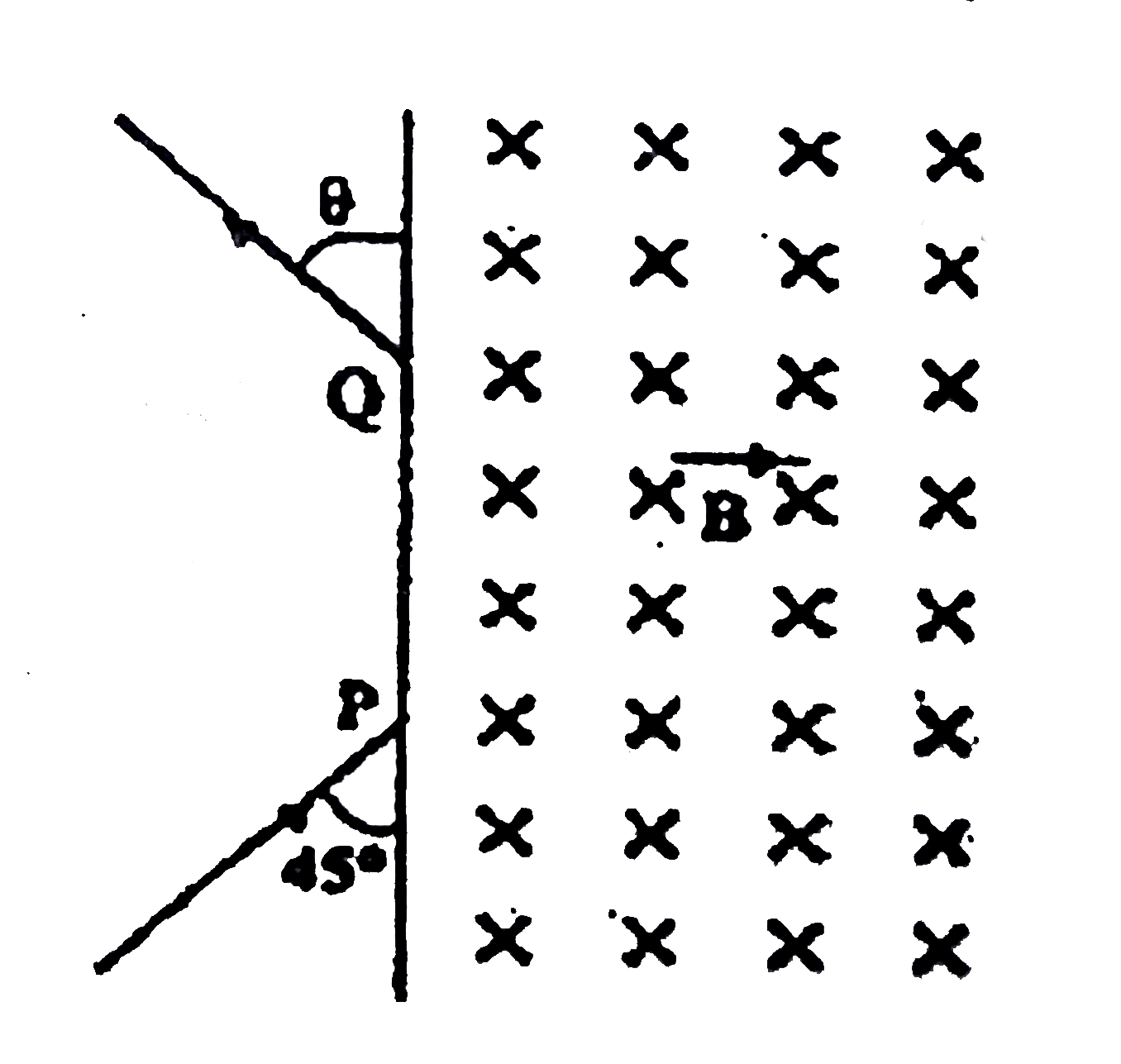
View SolutionA particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be
View SolutionA proton has a mass 1.67 ×10−27 kg and charge +1.6×10−19C. If the proton is accelerated through a potential difference of million volts, then the kinetic energy is
View SolutionA single electron system has ionization energy 1.118×107Jmol−1. Calculate the number of protons in the nucleus of the system .
View SolutionCalculate de Broglie wavelenth of a neutron
(mass, m=1.6×10−27 kg) moving with kinetic energy of 0.04 eV.
View SolutionTwo positively charged small particles, each of mass 1.7×10−27kg and carrying a charge of 1.6×10−19C are placed apart at a separation r. If each one experiences a repulsive force equal to its weight find their separation.
View SolutionThe de Broglie wavelength of neutrons in thermal equilibrium is (given mn=1.6×10−27kg)
View Solution