What is the wavelenth of the 0.186MeV gamma- ray photon emitted by radium .22688Ra?
To find the wavelength of the 0.186 MeV gamma-ray photon emitted by radium, we can use the relationship between energy and wavelength given by the equation:
E=hcλ
Where:
- E is the energy of the photon,
- h is Planck's constant (6.626×10−34Js),
- c is the speed of light (3×108m/s),
- λ is the wavelength.
Step 1: Convert the energy from MeV to Joules
The energy given is in MeV (mega electron volts). We need to convert this to Joules. The conversion factor is:
1eV=1.6×10−19J
Thus,
0.186MeV=0.186×106eV=0.186×106×1.6×10−19J
Calculating this gives:
E=0.186×106×1.6×10−19≈2.976×10−14J
Step 2: Rearrange the formula to solve for wavelength
We can rearrange the equation E=hcλ to solve for λ:
λ=hcE
Step 3: Substitute the known values into the equation
Now, substituting the values of h, c, and E:
λ=(6.626×10−34Js)(3×108m/s)2.976×10−14J
Step 4: Calculate the wavelength
Calculating the numerator:
hc=(6.626×10−34)(3×108)≈1.9878×10−25Js m
Now, substituting this into the equation for λ:
λ=1.9878×10−252.976×10−14≈6.67×10−12m
Final Answer
Thus, the wavelength of the 0.186 MeV gamma-ray photon emitted by radium is approximately:
λ≈6.67×10−12m
---
- E is the energy of the photon,
- h is Planck's constant (6.626×10−34Js),
- c is the speed of light (3×108m/s),
- λ is the wavelength.
The energy given is in MeV (mega electron volts). We need to convert this to Joules. The conversion factor is:
We can rearrange the equation E=hcλ to solve for λ:
Now, substituting the values of h, c, and E:
Calculating the numerator:
Thus, the wavelength of the 0.186 MeV gamma-ray photon emitted by radium is approximately:
Topper's Solved these Questions
- NUCLEAR PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:NUCLEAR PHYSICSExercise:Solved Examples
Explore 17 Videos
- NUCLEAR PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:NUCLEAR PHYSICSExercise:Exercise 5.1
Explore 10 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 5Exercise:Integer
Explore 12 Videos
- PHOTOELECTRIC EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:PHOTOELECTRIC EFFECTExercise:Integer Type
Explore 4 Videos
Similar Questions
A y-ray photon is emitted
View SolutionWhat is the ratio of the speed of gamma rays to that of radio waves in vacuum?
View SolutionWhat is the wavelength of light for the least energetic photon emitted in the Lyman series of the hydrogen spectrum. (Take , hc =1240 eV -nm)
View SolutionFind the momentum of a 12.0MeV photon.
View SolutionFigure below shows a simple diagram of a modern X ray tube. (i.e. Coolidge tube).
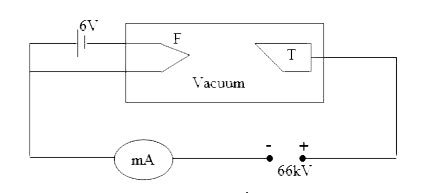
(i) Find the minimum wavelength of the X rays emitted by the X ray tube.
(ii) What will be the effect of replacing the 6V battery with a 9V battery on the emitted X rays?
View Solutionwhat are the frequency and wavelength of a photon emitted during a transition from n = 5 state to the n =2 state in the hydrogen atom?
View Solutionwhat are the frequency and wavelength of a photon emitted during a transition from n = 5 state to the n =2 state in the hydrogen atom?
View SolutionConsider the following nuclear fission reaction
.88Ra226→.86Rn222+.2He4+Q
In the fission reaction. Kinetic energy of α-particle is 4.44 MeV. Find the energy emitted as γ-radiation in keV in this reaction.
m(.88Ra226)=226.005 amu
m(.86Rn222)=222.000 amu
View Solution.12N beta decays to an ecited state of .12C, which subsequenctly decays to the ground state with the emission of a 4.43−MeV gamma ray. What is the maxium kinetic energy of the emitted beta particle?
View SolutionWhat is the minimum energy which a gamma ray photon must possess in order to produce electron positron pair ?
View Solution
