An electron in an H-atom kept at rest , jumps from the mth shell to the nth shell (m>n). Suppose instead of emitting electromagnetic wave, the energy reased is converted into the kinetic energy of the atom. Assume the Bohr model and conservation of angular momentum are valid. If I is the moment of inertia the angular velocity of the atom about the nucleus is 4(m−n)h/kI. Calculate k
The correct Answer is:8
To solve the problem, we will follow these steps:
Step 1: Understand the Energy Transition
When an electron jumps from the m-th shell to the n-th shell in a hydrogen atom, it releases energy. According to the Bohr model, the energy of an electron in the nth shell is given by:
En=−13.6eVn2
The energy difference when the electron transitions from the m-th shell to the n-th shell is:
ΔE=En−Em=−13.6eVn2+13.6eVm2=13.6eV(1n2−1m2)
Step 2: Convert Energy to Kinetic Energy
The energy released during the transition is converted into kinetic energy of the atom. Thus, we have:
ΔE=KE=12Iω2
where I is the moment of inertia and ω is the angular velocity of the atom about the nucleus.
Step 3: Angular Momentum Conservation
According to the conservation of angular momentum, the change in angular momentum due to the transition can be expressed as:
Lm−Ln=Iω
where Lm=mh2π and Ln=nh2π. Therefore, the change in angular momentum is:
ΔL=Lm−Ln=mh2π−nh2π=(m−n)h2π
Step 4: Relate Angular Momentum to Angular Velocity
From the conservation of angular momentum, we have:
ΔL=Iω
Substituting the expression for ΔL:
(m−n)h2π=Iω
From this, we can express ω:
ω=(m−n)h2πI
Step 5: Compare with Given Angular Velocity
The problem states that the angular velocity is given by:
ω=4(m−n)hkI
Setting the two expressions for ω equal to each other gives:
(m−n)h2πI=4(m−n)hkI
Step 6: Solve for k
Assuming m≠n and h≠0, we can cancel (m−n)h and I from both sides:
12π=4k
Cross-multiplying gives:
k=8π
Final Answer
Thus, the value of k is:
8π
When an electron jumps from the m-th shell to the n-th shell in a hydrogen atom, it releases energy. According to the Bohr model, the energy of an electron in the nth shell is given by:
En=−13.6eVn2
The energy difference when the electron transitions from the m-th shell to the n-th shell is:
ΔE=En−Em=−13.6eVn2+13.6eVm2=13.6eV(1n2−1m2)
The energy released during the transition is converted into kinetic energy of the atom. Thus, we have:
ΔE=KE=12Iω2
where I is the moment of inertia and ω is the angular velocity of the atom about the nucleus.
According to the conservation of angular momentum, the change in angular momentum due to the transition can be expressed as:
Lm−Ln=Iω
where Lm=mh2π and Ln=nh2π. Therefore, the change in angular momentum is:
ΔL=Lm−Ln=mh2π−nh2π=(m−n)h2π
From the conservation of angular momentum, we have:
ΔL=Iω
Substituting the expression for ΔL:
(m−n)h2π=Iω
From this, we can express ω:
ω=(m−n)h2πI
The problem states that the angular velocity is given by:
ω=4(m−n)hkI
Setting the two expressions for ω equal to each other gives:
(m−n)h2πI=4(m−n)hkI
Assuming m≠n and h≠0, we can cancel (m−n)h and I from both sides:
12π=4k
Cross-multiplying gives:
k=8π
Thus, the value of k is:
8π
Topper's Solved these Questions
- ATOMIC PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:ATOMIC PHYSICSExercise:Integer
Explore 4 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:ATOMIC PHYSICSExercise:Fill In The Blanks
Explore 8 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:ATOMIC PHYSICSExercise:Multiple Correct
Explore 13 Videos
- ALTERNATING CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:ALTERNATING CURRENTExercise:Single Correct
Explore 10 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
Similar Questions
The electrons in a H- atom kept at rest , jumps from the mth shell to the nth shell (m>n). Suppose instead of emitting electromagnetic wave, the energy released is converted into kinetic energy of the atom. Assuming Bohr's model and conservation of angular momentum are valid. Now , answer the following questions:
Calculate the angular velocity of the atom about the nucleus if l is the momentum of inertia
View SolutionThe electrons in a H- atom kept at rest , jumps from the mth shell to the nth shell (m>n). Suppose instead of emitting electromagnetic wave, the energy released is converted into kinetic energy of the atom. Assuming Bohr's model and conservation of angular momentum are valid. Now , answer the following questions:
What principal is violated of inertia
View SolutionThe electrons in a H- atom kept at rest , jumps from the mth shell to the nth shell (m>n). Suppose instead of emitting electromagnetic wave, the energy released is converted into kinetic energy of the atom. Assuming Bohr's model and conservation of angular momentum are valid. Now , answer the following questions:
If the above comprehension be true , ehat is not valid here?
View SolutionIn an atom when an electron jumps from K-shel to M-shell
View Solution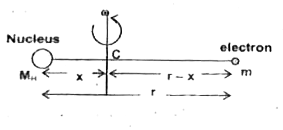
The angular momentum of the atom about the centre of mass will be
View SolutionThe angular momentum of a body with mass (m) moment of inertia (I) and angular velocity (ω) rad/s is equal to
View SolutionAn electron in H atom jumps from the third energy level to the first energy .The charge in the potential energy of the electron is
View SolutionA body is rotating with angular momentum L. If I is its moment of inertia about the axis of rotation is I, its kinetic energy of rotation is
View SolutionThe rotational kinetic energy of a body is E and its moment of inertia is I. The angular momentum is
View SolutionIf the magnitude of energy of the electron in nth Bohr orbit is EnandJn is its angular momentum , then
View Solution
