Question

An electron is orbiting is a circular orbit of radius r under the influence of a constant magnetic field of strength B. Assuming that Bohr postulate regarding the quantization of angular momentum holds good for this electron, find
(a) the allowed values of te radius r of the orbit.
(b) the kinetic energy of the electron in orbit
(c ) the potential energy of interaction between the magnetic moment of the orbital current due to the electron moving in its orbit and the magnetic field B.
(d) the total energy of the allowed energy levels.
(e) the total magnetic flux due to the magnetic field B passing through the nth orbit. (Assume that the charge on the electron is -e and the mass of the electron is m).

Answer

a `sqrt n a_(0)`, (b). `(1)/(2)nh ((e B)/(m))`, ( c).`(1)/(2)nh ((e B)/(m))` d.`nh ((e B)/(m))`, e.`((nh)/(2 e))`

Explanation

`(mv^(2))/( r) = e VB`
or `vr = (v)/( R) = (c B)/(m) (i)`
Using Bohr quantization condition.
`mvr = (nh)/(2 pi) = nh, to`integer
or `vr = (nh)/(m)` (ii)

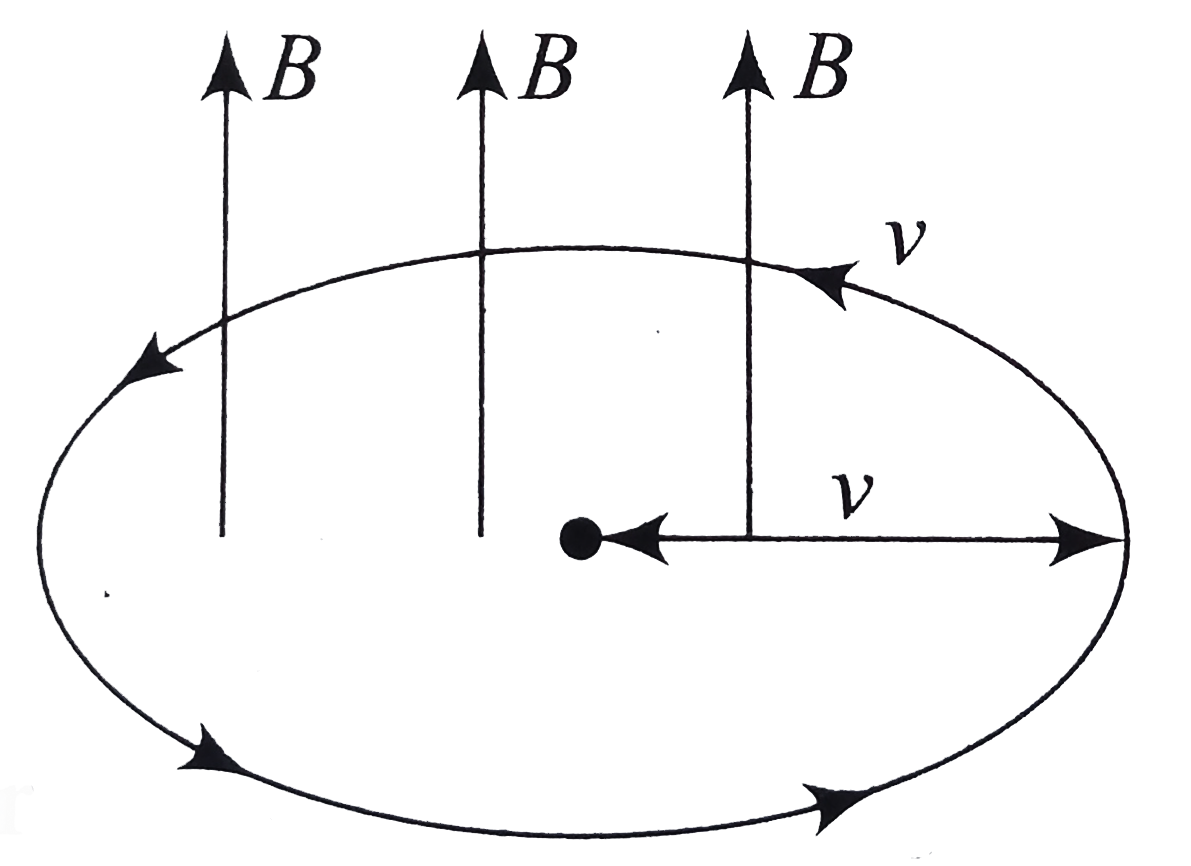
a. `r^(2) = (nh)/(Be)`
or `r = sqrt n sqrt((h)/(Be)) = sqrt n a_(0)` (iii)
b. `T ("kinetic energy") = (1)/(2) mv^(2)`
`= (m^(2) v^(2))/(2 m) = (1)/(2 m) xx (n^(2) h^(2))/(r^(2))`
`= (1)/(2 m) xx 2 h Be = (1)/(2) nh ((Be)/(m))` (iv)
c.
The time period of revolution of the electron.
`tau = (2 pi r)/(v) = (2 pi m)/(Be)`
The corrent, `i = (e)/(tau) = (e^(2) B)/(2 pi m) = (e)/(2 m) nh`
The potential energy of interaction
`U = - bar mu barB = (1)/(2)nh ((e B)/(m))` (v)
d. The total energy .
`E = T + U = nh ((e B)/(m))` which is quantized.
e. The total magnetic flux through the nth orbit.
`phi = pi r^(2) B = pi ((nh)/(Be))` (vi)