Two identical metal plates show photoelectric effect. Light of wavelength λA falls on plate A and λB fall on plate B lamaA=2λB, The maximum KE of the photoelectrons are KA and KB, respectively, Which one of the following is true?
2KA=KB
KA=2KB
(KA<KB2)
KA>2KB
The correct Answer is:C
To solve the problem, we need to analyze the photoelectric effect for two plates A and B with different wavelengths of light falling on them. The relationship between the kinetic energy of the emitted photoelectrons and the wavelength of the incident light is given by the photoelectric equation:
K=hcλ−Φ
where:
- K is the maximum kinetic energy of the emitted photoelectrons,
- h is Planck's constant,
- c is the speed of light,
- λ is the wavelength of the incident light,
- Φ is the work function of the metal.
1. Identify the Wavelengths:
We have two wavelengths:
- For plate A: λA
- For plate B: λB
Given that λA=2λB.
2. Write the Kinetic Energy Equations:
For plate A, the maximum kinetic energy KA can be expressed as:
KA=hcλA−Φ
For plate B, the maximum kinetic energy KB can be expressed as:
KB=hcλB−Φ
3. Substitute λA in Terms of λB:
Since λA=2λB, we can substitute this into the equation for KA:
KA=hc2λB−Φ
4. Express KA and KB in Terms of λB:
Now we can rewrite both kinetic energy equations:
- For plate A:
KA=hc2λB−Φ
- For plate B:
KB=hcλB−Φ
5. Compare KA and KB:
To compare KA and KB, we can subtract KA from KB:
KB−KA=(hcλB−Φ)−(hc2λB−Φ)
Simplifying this gives:
KB−KA=hcλB−hc2λB=hc2λB
6. Conclusion:
Since KB−KA=hc2λB>0, it follows that:
KB>KA
Therefore, the maximum kinetic energy of the photoelectrons from plate B is greater than that from plate A.
Final Answer:
KB>KA
- K is the maximum kinetic energy of the emitted photoelectrons,
- h is Planck's constant,
- c is the speed of light,
- λ is the wavelength of the incident light,
- Φ is the work function of the metal.
We have two wavelengths:
- For plate A: λA
- For plate B: λB
Given that λA=2λB.
For plate A, the maximum kinetic energy KA can be expressed as:
KA=hcλA−Φ
For plate B, the maximum kinetic energy KB can be expressed as:
KB=hcλB−Φ
Since λA=2λB, we can substitute this into the equation for KA:
KA=hc2λB−Φ
Now we can rewrite both kinetic energy equations:
- For plate A:
KA=hc2λB−Φ
- For plate B:
KB=hcλB−Φ
To compare KA and KB, we can subtract KA from KB:
KB−KA=(hcλB−Φ)−(hc2λB−Φ)
Simplifying this gives:
KB−KA=hcλB−hc2λB=hc2λB
Since KB−KA=hc2λB>0, it follows that:
KB>KA
Therefore, the maximum kinetic energy of the photoelectrons from plate B is greater than that from plate A.
KB>KA
Topper's Solved these Questions
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Multiple Correct
10 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Linked Comprehension
44 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Subjective
16 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
Similar Questions
Two identical metal plates show photoelectric effect by a light of wavelength λA falling on plate A and λB on plate B(λA=2λB). The maximum kinetic energy is
View SolutionThe maximum KE of photoelectrons emitted from a cetain metallic surface is 30 eV when monochromatic radiation of wavelength λ falls on it. When the same surface is illuminated with light of wavelength 2λ, the minimum KE of photoelectrons is found to be 10 eV. (a) Calculate the wavelength λ and (b) determine the maximum wavelength of incident radiation for which photoelectric emission is possible.
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View SolutionThe frequency of incident light falling on a photosensitive metal plate is doubled, the KE of the emitted photoelectrons is
View SolutionLight of wavelength 5000Å falls on a sensitive plate with photoelectric work function of 1.9eV. The kinetic energy of the photoelectron emitted will be
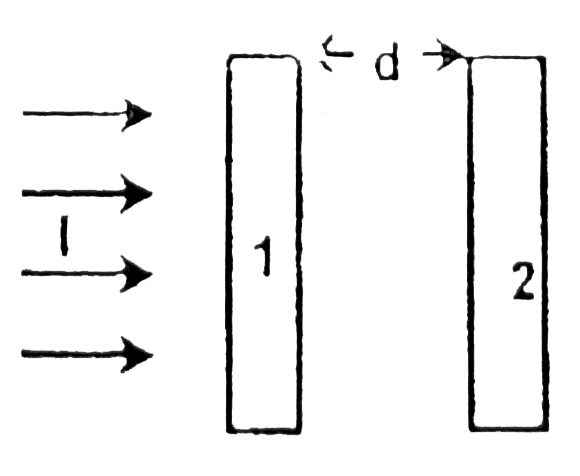
View SolutionTwo parallel large metal plates, each of area A are piaced at a distance d apart. Light of intensity I and wavelength λ falls on the plate 1 which is photosensitive. The efficiency of photoelectron emission is 100%. The photoelectrons are immediately swept away from plate 1 in such a way that the plate 2 remains neutral. Find the potential difference between the two plates at any time t, if plate 1 is neutral initially.
View SolutionIn an experiment on photoelectric effect light of wavelength 400nm is incident on a metal plate at rate of 5W. The potential of the collector plate is made sufficiently positive with respect to emitter so that the current reaches the saturation value. Assuming that on the average one out of every 106 photons is able to eject a photoelectron, find the photocurrent in the circuit.
View SolutionThe work function (ϕ) of some metals is listed below . The number of metals which will show photoelectric effect when light of 300 nm wavelength falls on the metal is :

View SolutionWork function of a metal surface is ϕ=1.5eV. If a light of wavelength 5000Å falls on it then the maximum K.E. of ejected electron will be-
View SolutionTwo flasks A and B of equal volume are at temperature 100K and 200K containing H2 and CH4, respectively. Which of the following is true about KE per mole (KE= Kinetic energy).
View Solution
