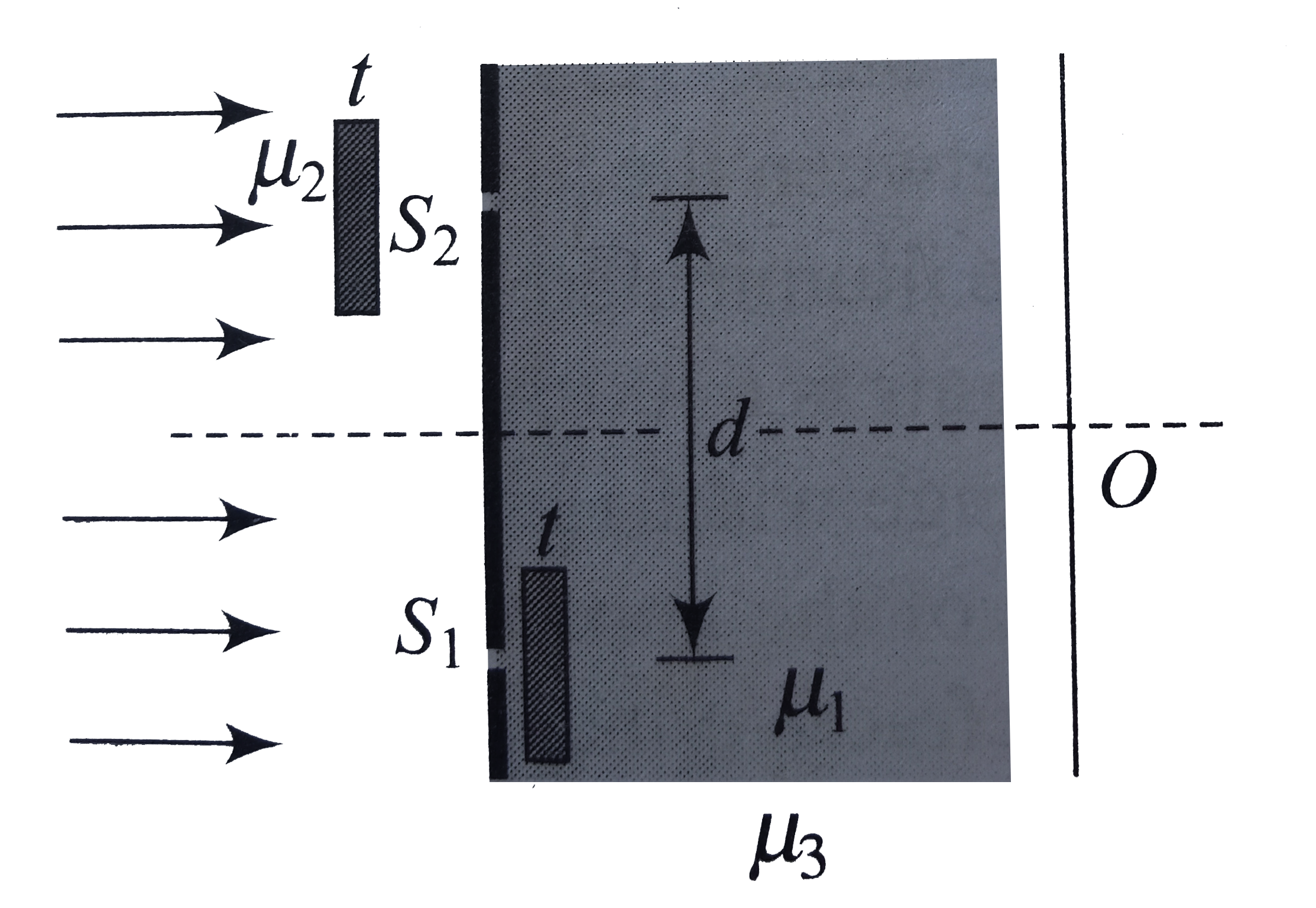
A Young's double slit apparatus is immersed in a liquid of refractive index μ1. The slit plame touches the liquid surface. A parallel beam of monochromatic light of wavelength λ (in air) is incident normally on the slits.
a. Find the fringe width.
b. If one of the slits (say S2) is covered by a transparent slab of refrative index μ2 and thickless t as shown, find the new position of central maxima.
c. Now, the other slit, S1 is also covered by a slab of same thickness and refractive index μ3 as shown in Fig. 2.49 due to which the central maxima recovers it positon, find the value of μ3
Find the ratio of intensities at O in the three conditions (a), (b), and (c).
Fringe width, w=λμDd=λDμ1d
Position of central maximum is shifted upward by a distance (μ2−1)tDd
c. (μ2−1)tDd=(μ3μ1−1)tDd⇒μ2μ1 or μ3=μ1μ2
b. I=Imaxcos2(ϕ2), where ϕ=(2πλ)Δx or ϕ2=(πλ)Δx
⇒I∝cos2(ϕ2)
The the first and third case, Δx=0 while in the second case, Δx=(μ2−1)t. Therefore, the desired ratio is
I1:I2:I3=1:cos2{π(μ2−1)tλ}:1
 .
.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Solved Examples
10 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.1
12 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
When entire Young's double slit apparatus is immersed in a liquid the fringe width decreases by 20∘. The refractive index of the liquid is
View SolutionA young's double slit apporatus is immersed in a liquid of refractive index 1.33.It has slit separation of 1 mm and interference pattern is observed on the screen at a distance 1.33 m from plane of slits.The wavelength in air is 6300Å
Calculate the fringe width.
View SolutionA double - slit apparatus is immersed in a liquid of refractive index 1.33 it has slit separation of 1mm and distance between the plane of slits and screen 1.33 m the slits are illuminated by a parallel beam of light whose wavelength in air is 800 nm.
(i) Calculate the fringe width.
(ii) One of the slits of apparatus is covered by a thin glass sheet of refractive index 1.53 Find the smallest thickness of the sheet to bring the adjacent minima on the axis.
View SolutionA parallel beam of monochromatic light of wavelength 500 nm is incident normally on a rectangular slit. The angular width of the central fringe of Fraunhofer diffraction is found to be 60∘. Find the width of the slit in metre.
View SolutionA young's double slit apporatus is immersed in a liquid of refractive index 1.33.It has slit separation of 1 mm and interference pattern is observed on the screen at a distance 1.33 m from plane of slits.The wavelength in air is 6300Å
One of the slits of the apparatus is covered by a thin glass sheet of refractive index 1.53. Find the smallest thickness of the sheet to interchange the position of minima and maxima .
View SolutionA young's double slit apporatus is immersed in a liquid of refractive index 1.33.It has slit separation of 1 mm and interference pattern is observed on the screen at a distance 1.33 m from plane of slits.The wavelength in air is 6300Å
One of the slits of the apparatus is covered by a thin glass sheet of refractive index 1.53. Find the fringe width
View SolutionIn YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
View SolutionIn Young's double slit experiment with light of wavelength λ=600nm, intensity of central fringe is I0. Now one of the slit is covered by glass plate of refractive index 1.4 and thickness t=5μm. The new intensity at the same point on screen will be :
View SolutionIn the YDSE shown the two slits are covered with thin sheets having thickness t & 2t and refractive index 2μ and μ .Find the position (y) of central maxima.

View SolutionA double-slit experiment is immersed in a liquid of refractive index 1.33. The separation between the slits is 1mm and the distance between the slits and screen is 1.33 m. If slits are illuminated by a parallel beam of light whose wavelength is 6300Å, then fringe width will be
View Solution
