When an object is placed on the principal axis of a convex lens at two different positins, it produces the images with magnifications +2 and −4 respectively. How many times more away from the lens the image will be formed in the second position as compared to the first postion?
2
4
5
10
The correct Answer is:c.
To solve the problem step by step, we will utilize the magnification formula and the lens formula for a convex lens.
Step 1: Understanding the Magnification
The magnification (m) produced by a lens is given by the formula:
m=VU
where V is the image distance and U is the object distance.
Step 2: Setting Up the First Position
For the first position, the magnification is given as +2:
m1=2=V1U1
Let U1=−X (the object distance is taken as negative in lens convention). Therefore, we can write:
V1=2U1=2(−X)=−2X
Step 3: Using the Lens Formula for the First Position
The lens formula is given by:
1V−1U=1F
Substituting V1 and U1:
1−2X−1−X=1F
This simplifies to:
−12X+1X=1F
Combining the fractions:
−1+22X=1F
Thus:
12X=1F
From this, we find:
F=2X
Step 4: Setting Up the Second Position
For the second position, the magnification is given as −4:
m2=−4=V2U2
Let U2=−Y. Therefore, we can write:
V2=−4U2=−4(−Y)=4Y
Step 5: Using the Lens Formula for the Second Position
Using the lens formula again:
1V2−1U2=1F
Substituting V2 and U2:
14Y−1−Y=1F
This simplifies to:
14Y+1Y=1F
Combining the fractions:
1+44Y=1F
Thus:
54Y=1F
From this, we find:
F=4Y5
Step 6: Equating Focal Lengths
Since the focal length F is the same for both positions, we can equate the two expressions for F:
2X=4Y5
Step 7: Finding the Ratio of Distances
From the equation 2X=4Y5, we can rearrange it to find the ratio of Y to X:
4Y=10X
Dividing both sides by 4:
Y=10X4=5X2
Step 8: Finding the Ratio of Image Distances
Now, we want to find how many times more away from the lens the image will be formed in the second position as compared to the first position:
V2V1=4Y−2X
Substituting Y=5X2:
V2V1=4⋅5X2−2X=10X−2X=−5
Conclusion
The absolute value of the ratio of the distances of the images formed in the second position to that of the first position is:
|V2||V1|=5
Thus, the image will be formed 5 times more away from the lens in the second position compared to the first position.
The magnification (m) produced by a lens is given by the formula:
m=VU
where V is the image distance and U is the object distance.
For the first position, the magnification is given as +2:
m1=2=V1U1
Let U1=−X (the object distance is taken as negative in lens convention). Therefore, we can write:
V1=2U1=2(−X)=−2X
The lens formula is given by:
1V−1U=1F
Substituting V1 and U1:
1−2X−1−X=1F
This simplifies to:
−12X+1X=1F
Combining the fractions:
−1+22X=1F
Thus:
12X=1F
From this, we find:
F=2X
For the second position, the magnification is given as −4:
m2=−4=V2U2
Let U2=−Y. Therefore, we can write:
V2=−4U2=−4(−Y)=4Y
Using the lens formula again:
1V2−1U2=1F
Substituting V2 and U2:
14Y−1−Y=1F
This simplifies to:
14Y+1Y=1F
Combining the fractions:
1+44Y=1F
Thus:
54Y=1F
From this, we find:
F=4Y5
Since the focal length F is the same for both positions, we can equate the two expressions for F:
2X=4Y5
From the equation 2X=4Y5, we can rearrange it to find the ratio of Y to X:
4Y=10X
Dividing both sides by 4:
Y=10X4=5X2
Now, we want to find how many times more away from the lens the image will be formed in the second position as compared to the first position:
V2V1=4Y−2X
Substituting Y=5X2:
V2V1=4⋅5X2−2X=10X−2X=−5
The absolute value of the ratio of the distances of the images formed in the second position to that of the first position is:
|V2||V1|=5
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
An object is placed at a distance of f/2 from a convex lens. The image will be
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View SolutionAn illuminated object is placed on the principal axis of a converging lens so that real image is formed on the other side of the lens. If the object is shifted a little,
View SolutionAn object of length 2.0 cm is placed perpendicular to the principal axis of a convex lens of focal length 12 cm. Find the size of the image of the object is at a distance of 8.0 cm from the lens.
View SolutionAn object AB is placed between 2F1andF1 on the principal axis of a convex lens as shown in the diagram :
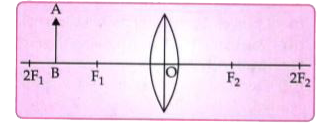
Copy the diagram and using three rays starting from point A, obtain the image of the object formed by the lens.
View SolutionAn object AB is placed between 2F, and F, on the principal axis of a convex lens as shown in the diagram.
Copy the diagram and using three rays starting from point A, obtain the image of the object formed by the lens.
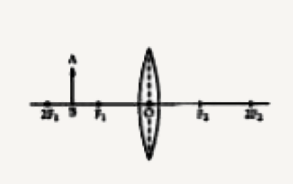
View SolutionAn equi-convex lens of focal length F in air is is cut into two halves along the plane perpendicular to the optic axis. One of the halves is placed between a fixed object and a screen separated by distance of 90 cm . Two images are formed on the screen for two different positions of the lens with magnification 2 and 1/2 respectively. Find the value of F . what would be the value of the focal length of the equiconvex lens if the lens is immersed in water ? Refractive index of the material of the lens is 1.5 and that of water is μw=4/3.
View SolutionAn object is placed at a distance of f2 from a convex lens of focal length f. The image will be
View SolutionA 4 cm tall object is placed on the principal axis of a convex lens. The distance of the
object from the optical centre of the lens 12 cm and its sharp image is formed at a
distance of 24 cm from it on a screen on the lens, in the which ways (towards the lens or away from the lens) will he have to move the screen to get a sharp image of the object on it again? How will the magnification of the image be affected ? .
View SolutionA point object moves along the principal axis of a convex lens of focal length f such that its real image, also formed on the principal axis at a distance 4f3 (at t=0) moves away from the lens with uniform velocity α. Find the velocity of the point object as a function of time t.
View Solution
