A lens(n=1.5) is 5cm thick and the radii of curvature of its object is placed at a distance of 12cm from the surface whose radius of curvature is 10cm. How far beyond the other surface is the image formed?
To solve the problem step by step, we will use the lens maker's formula and the concept of refraction at spherical surfaces.
Step 1: Identify the Given Values
- Refractive index of the lens, n=1.5
- Thickness of the lens, t=5cm
- Distance of the object from the first surface, u=−12cm (negative as per sign convention)
- Radius of curvature of the first surface, R1=+10cm (positive as it is convex)
- Radius of curvature of the second surface, R2=−25cm (negative as it is concave)
Step 2: Refraction at the First Surface
Using the refraction formula:
n2V−n1U=n2−n1R
where:
- n1=1 (air)
- n2=1.5 (lens)
- U=−12cm
- R=+10cm
Substituting the values:
1.5V−1−12=1.5−110
This simplifies to:
1.5V+112=0.510
1.5V+112=0.05
Now, convert 112 to a decimal:
1.5V+0.0833=0.05
Rearranging gives:
1.5V=0.05−0.0833
1.5V=−0.0333
Thus, solving for V:
V=1.5−0.0333≈−45cm
Step 3: Image Formation at the First Surface
The image formed by the first surface (let's call it I1) is located 45 cm on the same side as the object.
Step 4: Distance of the Image from the Second Surface
The distance of the image from the second surface:
u′=t+|V|=5cm+45cm=50cm
Since this is the object for the second surface, we take u′=−50cm (negative as per sign convention).
Step 5: Refraction at the Second Surface
Using the same refraction formula for the second surface:
n2V′−n1U′=n2−n1R2
where:
- n1=1.5
- n2=1
- U′=−50cm
- R2=−25cm
Substituting the values:
1V′−1.5−50=1−1.5−25
This simplifies to:
1V′+1.550=−0.5−25
1V′+0.03=0.02
Rearranging gives:
1V′=0.02−0.03
1V′=−0.01
Thus, solving for V′:
V′=1−0.01=−100cm
Step 6: Conclusion
The image is formed 100 cm on the opposite side of the second surface.
Final Answer
The image is formed 100 cm beyond the second surface.
---
- Refractive index of the lens, n=1.5
- Thickness of the lens, t=5cm
- Distance of the object from the first surface, u=−12cm (negative as per sign convention)
- Radius of curvature of the first surface, R1=+10cm (positive as it is convex)
- Radius of curvature of the second surface, R2=−25cm (negative as it is concave)
Using the refraction formula:
n2V−n1U=n2−n1R
where:
- n1=1 (air)
- n2=1.5 (lens)
- U=−12cm
- R=+10cm
1.5V−1−12=1.5−110
This simplifies to:
1.5V+112=0.510
1.5V+112=0.05
Now, convert 112 to a decimal:
1.5V+0.0833=0.05
Rearranging gives:
1.5V=0.05−0.0833
1.5V=−0.0333
Thus, solving for V:
V=1.5−0.0333≈−45cm
The image formed by the first surface (let's call it I1) is located 45 cm on the same side as the object.
The distance of the image from the second surface:
u′=t+|V|=5cm+45cm=50cm
Since this is the object for the second surface, we take u′=−50cm (negative as per sign convention).
Using the same refraction formula for the second surface:
n2V′−n1U′=n2−n1R2
where:
- n1=1.5
- n2=1
- U′=−50cm
- R2=−25cm
1V′−1.5−50=1−1.5−25
This simplifies to:
1V′+1.550=−0.5−25
1V′+0.03=0.02
Rearranging gives:
1V′=0.02−0.03
1V′=−0.01
Thus, solving for V′:
V′=1−0.01=−100cm
The image is formed 100 cm on the opposite side of the second surface.
The image is formed 100 cm beyond the second surface.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.6
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.7
21 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.4
12 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A point object is placed at a distance 20 cm from the focus of a concave mirror of radius of curvature 20 cm. Find the distance (in cm) of the image from the focus.
View SolutionAn object is placed at 4 cm distance in front of a concave mirror of radius of curvature 24 cm. Find the position of image. Is the image magnified?
View SolutionAn object 2.5 cm high is placed at a distance of 10 cm from a concave mirror of radius of curvature 30 cm The size of the image is
View SolutionAn image is formed at a distance of 100 cm from the glass surface with refractive index 1.5, when a point object is placed in the air at a distance of 100 cm from the glass surface. The radius of curvature is of the surface is
View SolutionFind the position, magnification and nature of the image of an object placed at a distance of 8 cm from a convex mirror of radius of curvature 24 cm.
View SolutionIn a medium of refractive index 1.6 and having a convex surface has a point object in it at a distance of 12 cm from the pole. The radius of curvature is 6 cm. Locate the image as seen from air
View SolutionA point object is placed at a distance of 20cm from a thin plano-convex lens of focal length 15cm(μ=1.5). The curved surface is silvered. The image will form at
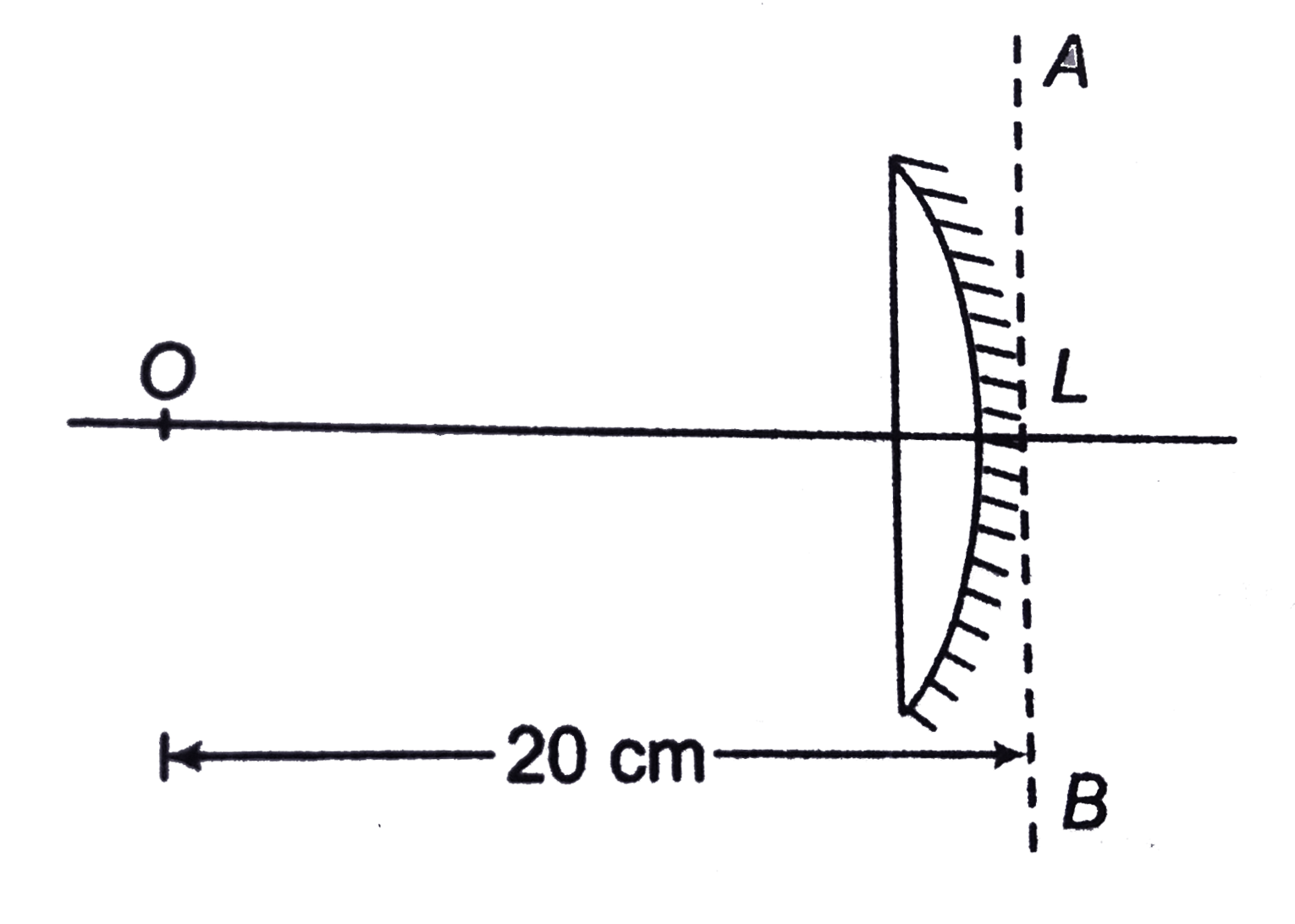
View SolutionA point object is placed at a distance of 20cm from a thin plano-convex lens of focal length 15cm(μ=1.5). The curved surface is silvered. The image will form at

View SolutionAn object 5.0cm in length is placed at a distance of 20cm in front of a convex mirror of radius of curvature 30cm. Find the position of image, its nature and size.
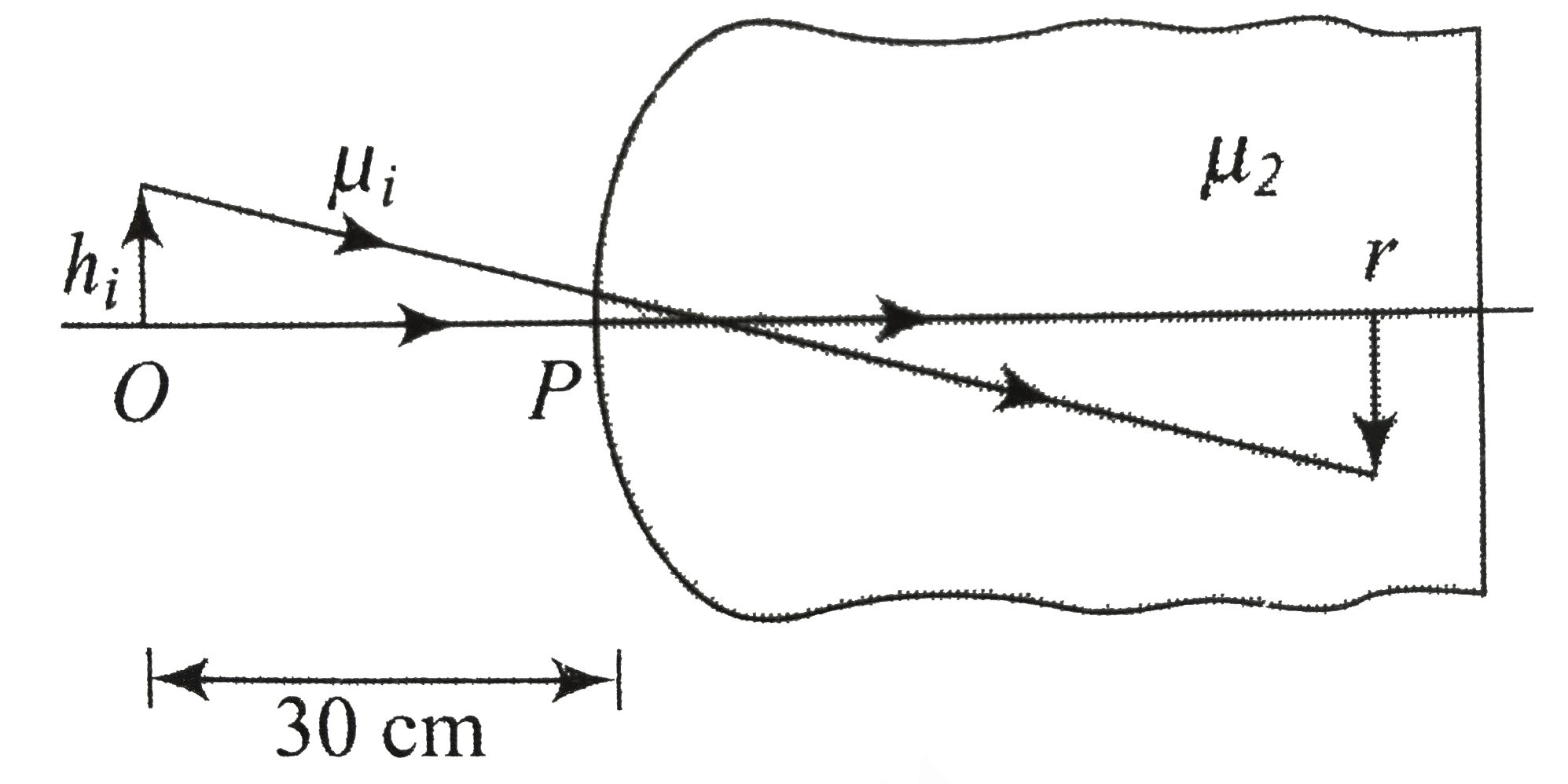
View SolutionA small object of height 0.5 cm is placed in front of a convex surface of glass (μ−1.5) of radius of curvature 10cm. Find the height of the image formed in glass.
View Solution
