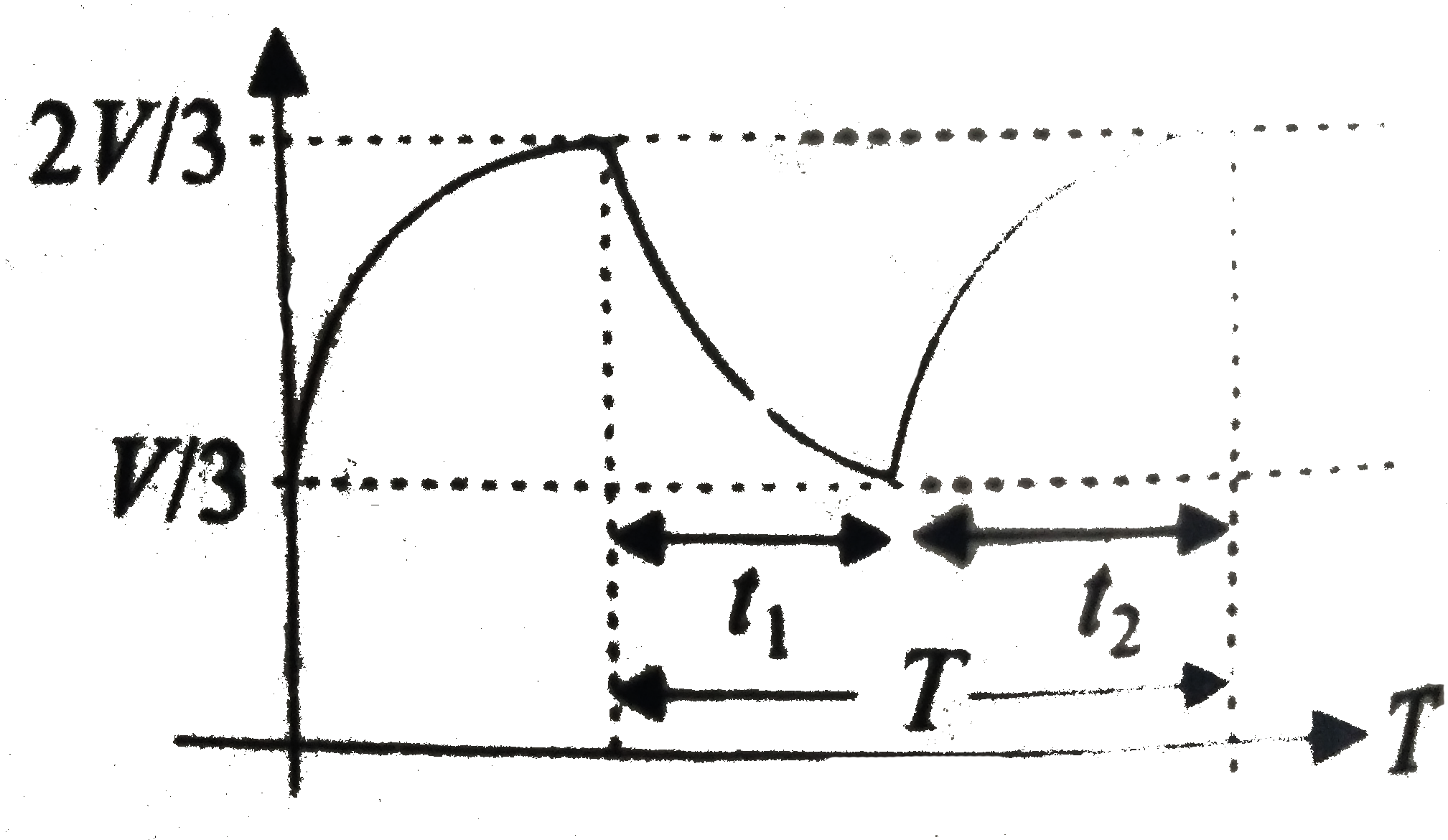
VC is the ideal voltmeter in the figure. Resistance of the resistor shown is R. Initially the switch is in position 2 when charging of the capacitor starts. Initially the capacitor was uncharged. The switch in circuit shifts automatically from 2 to 1 when VC>2V/3 and goes back to 2 from 1 when VC<V/3. The ideal voltmeter reads voltage across capacitor as plotted. What is the period T of the wave from in terms of R and C ?
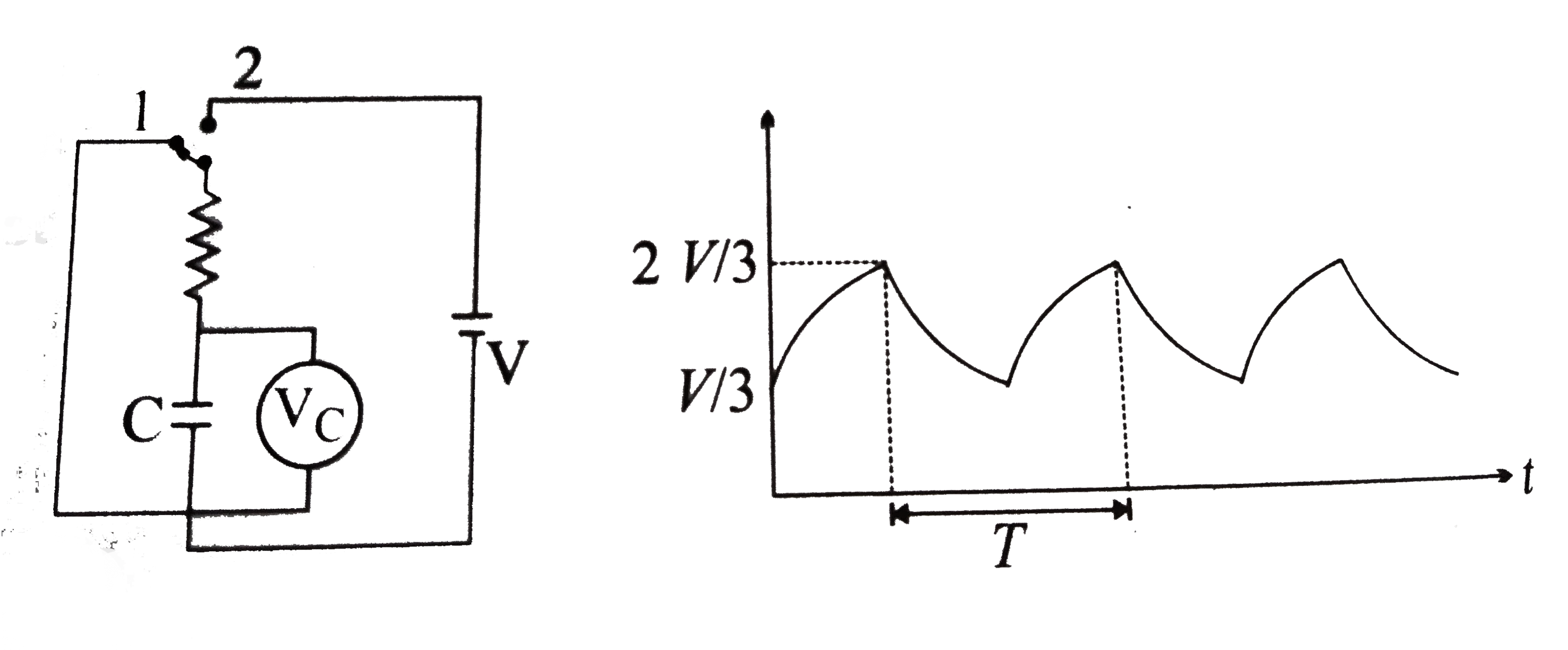 ,
,
3RC1n3
2RC1n2
(RC/2)1n2
none of these
The correct Answer is:B
b. t1 is the time of capacitor to discharge from 2V/3 to V/3.
For this , V3=2V2e−t1/τ or t1=τ1n2=RC1n2
t2 is time for charging of capacitor
from V/3to2V/3.
So ∫2VC/3VC/3dqVC−q=∫t20dtRC
or t2=RC1n2
T=t1+t2=2RC1n2
 .
.
Similar Questions
The switch in Figure (a) closes when Vc=2V/3 and opens when Vc=V/3. The voltmeter reads a voltage as plotted in figure (b). What is the period T of the waveform? (take R1=6R and R2=3R, and ln2=0.7 if required)
(a)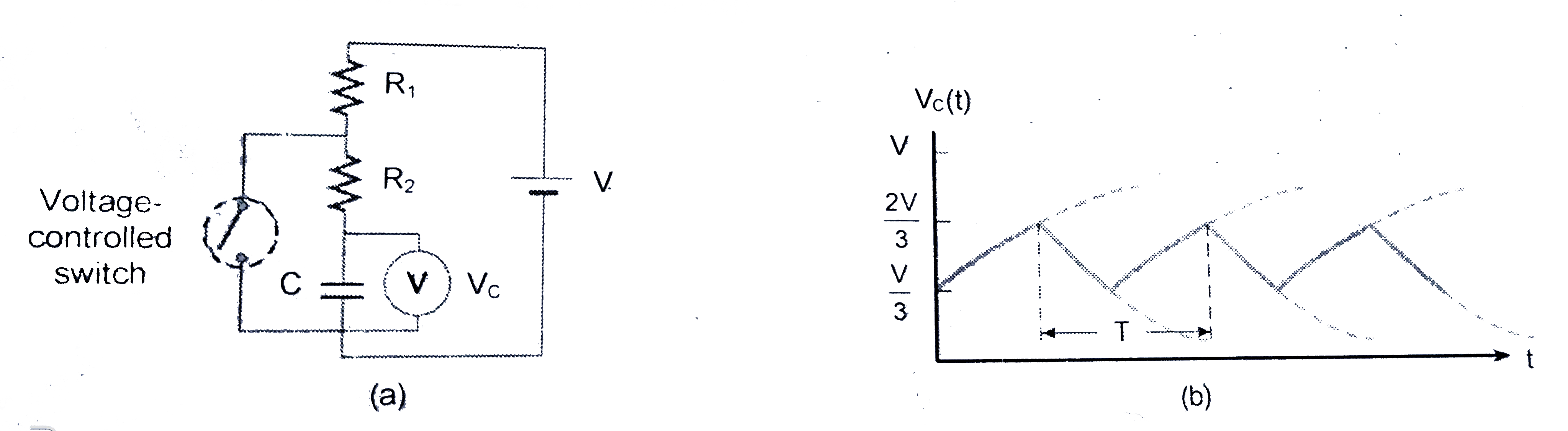
View SolutionCondsider
 .
.
In the circuit shown is the switch can be shifted to positions 1 and 2 The charge on capacitor C1 when the switch is at position 1 is.
View SolutionIf the reading of the ideal voltmeter shown in the circuit is 2V the internal resistance of the two identical cells is
_2019_CBT5_E01_030_Q01.png)
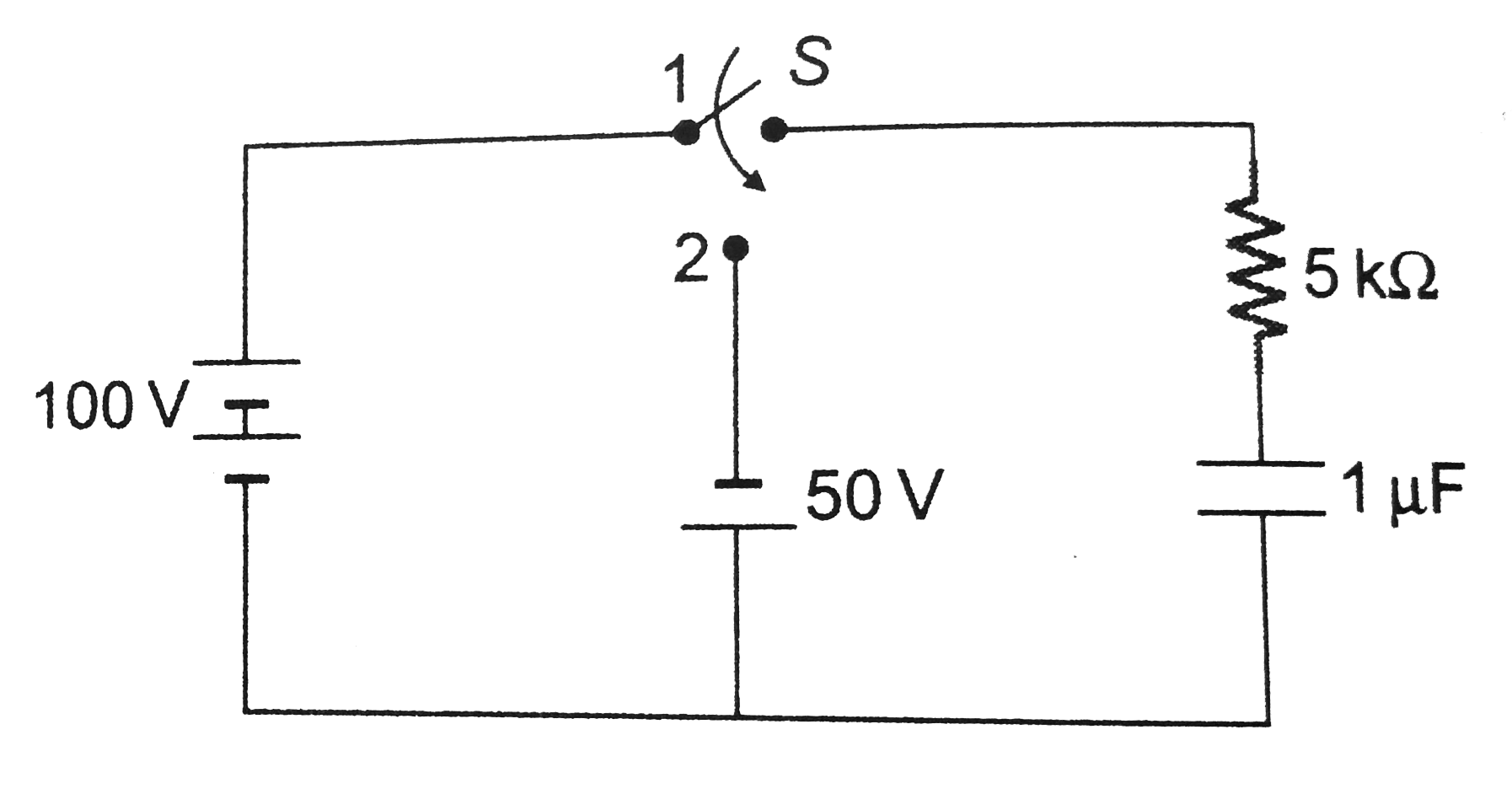
View SolutionInitially, the switch is in position 1 for a long time. At t=0, the switch is Obtain expressions for VC and VR for t>0
View SolutionThe capacitor C shown in the figure is in steady state condition when switch is shifted from position 1 to position 2.The heat liberated in the process is
_PHY_E05_272_Q01.png)
View SolutionIn the R-C circuit shown in the figure the total of 3.6×10−3J is dissipated in the 10 ohms resistor when the switch S is closed. The initial charge on the capacitor is

View SolutionPassage-III
In the circuit shown, the battery is ideal with emf V. The capacitor is initially uncharged. The switch is closed at time t = 0
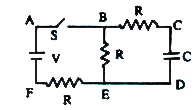
The current in the branch BE at t=∞ is
View SolutionPassage-III
In the circuit shown, the battery is ideal with emf V. The capacitor is initially uncharged. The switch is closed at time t = 0
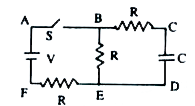
The current in branch containing capacitors at any time t is
View SolutionIn the given figure switch is open initially and capacitor C2 is unchanged
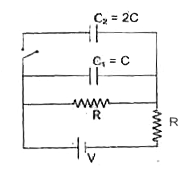
Charge on C2 just after closing the switch is
View SolutionIn the circuit shown in the figure, the total charge is 750μC and the voltage across capacitor C2 is 20 V. Then the charge on capacitor C2 is:
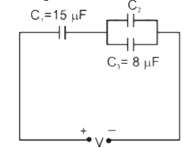
View Solution
