A parallel plate air capacitor is connected to a battery. The quantities charge, voltage, electric field and energy associated with this capacitor are given by Q0 , V0, E0 and U0 respectively. A dielectric slab is now introduced to fill the space between the plates with battery still in connection. The corresponding quantities now given by Q, V, E and U are related to the previous one as
Q>Q0
V>V0
E>E0
U>U0
To solve the problem, we need to relate the quantities associated with a parallel plate capacitor before and after introducing a dielectric slab while the capacitor remains connected to a battery. The quantities we will consider are charge (Q), voltage (V), electric field (E), and energy (U).
1. Initial Conditions:
- The initial quantities for the air capacitor connected to a battery are:
- Charge: Q0
- Voltage: V0
- Electric Field: E0
- Energy: U0
2. Voltage with Dielectric:
- When the dielectric slab is introduced while the battery is still connected, the voltage across the capacitor remains the same because the battery maintains a constant voltage.
- Therefore, we have:
V=V0
3. Capacitance with Dielectric:
- The capacitance of the capacitor with the dielectric slab becomes:
C=C0⋅K
- Here, K is the dielectric constant of the slab, and C0 is the capacitance of the capacitor without the dielectric.
4. Charge with Dielectric:
- The charge on the capacitor can be expressed as:
Q=C⋅V
- Substituting for C and using the fact that V=V0:
Q=(C0⋅K)⋅V0
- Since the initial charge was Q0=C0⋅V0, we can express the charge with the dielectric as:
Q=K⋅Q0
5. Electric Field with Dielectric:
- The electric field E in a parallel plate capacitor is given by:
E=Vd
- Since V=V0 and the distance d between the plates remains unchanged, we have:
E=V0d=E0
6. Energy with Dielectric:
- The energy stored in the capacitor can be expressed as:
U=12CV2
- Substituting for C and V:
U=12(C0⋅K)V20
- Since U0=12C0V20, we can express the energy with the dielectric as:
U=K⋅U0
Summary of Relationships:
- Charge: Q=K⋅Q0
- Voltage: V=V0
- Electric Field: E=E0
- Energy: U=K⋅U0
- The initial quantities for the air capacitor connected to a battery are:
- Charge: Q0
- Voltage: V0
- Electric Field: E0
- Energy: U0
- When the dielectric slab is introduced while the battery is still connected, the voltage across the capacitor remains the same because the battery maintains a constant voltage.
- Therefore, we have:
V=V0
- The capacitance of the capacitor with the dielectric slab becomes:
C=C0⋅K
- Here, K is the dielectric constant of the slab, and C0 is the capacitance of the capacitor without the dielectric.
- The charge on the capacitor can be expressed as:
Q=C⋅V
- Substituting for C and using the fact that V=V0:
Q=(C0⋅K)⋅V0
- Since the initial charge was Q0=C0⋅V0, we can express the charge with the dielectric as:
Q=K⋅Q0
- The electric field E in a parallel plate capacitor is given by:
E=Vd
- Since V=V0 and the distance d between the plates remains unchanged, we have:
E=V0d=E0
- The energy stored in the capacitor can be expressed as:
U=12CV2
- Substituting for C and V:
U=12(C0⋅K)V20
- Since U0=12C0V20, we can express the energy with the dielectric as:
U=K⋅U0
- Charge: Q=K⋅Q0
- Voltage: V=V0
- Electric Field: E=E0
- Energy: U=K⋅U0
Similar Questions
A parallel plate capacitor is connected across a battery. Now, keeping the battery connected, a dielectric slab is inserted between the plates. In the process,
View SolutionTwo large conducting plates of a parallel plate capacitor are given charges Q and 3Q respectively. If the electric field in the region between the plates is E0 , then the force of interaction between the plates is

View Solution
Knowledge Check
A parallel plate capacitor of capacity 5μF and plate separation 6cm is connected to a 1V battery and is charged. A dielectric of dielectric constant 4 and thickness 4cm is introduced into the capacitor. The additional charge that flows into the capacitor from the battery is.
A2μCB3μCC5μCD10μC
An uncharged parallel plate capacitor is connected to a battery. The electric field between the plates is 10V/m. Now a dielectric of dielectric constant 2 is inserted between the plates filling the entries space. The electric field between the plates now is
View SolutionThe plates of a parallel plate capacitor with no dielectirc are connected to a volatage source. Now a dielectric of dielectric constant K is inserted to fill the whose space between the plates with voltage source remainign connected to the capacitor-
View SolutionAnswer the following:
(a) When a parallel plate capacitor is connected across a dc battery, explain briefly how the capacitor gets charged.
(b) A parallel plate capacitor of capacitance 'C' is charged to 'V' volt by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant 1<k<2 is introduced to fill the space between the plates. How will the following be affected ?
(i) The electric field between the plates of the capacitor.
(ii) The energy stored in the capacitor. Justify your answer in each case.
(c) The electric potential as a function of distance 'x' is shown in the figure. Draw a graph of the electric field E as a function of x.
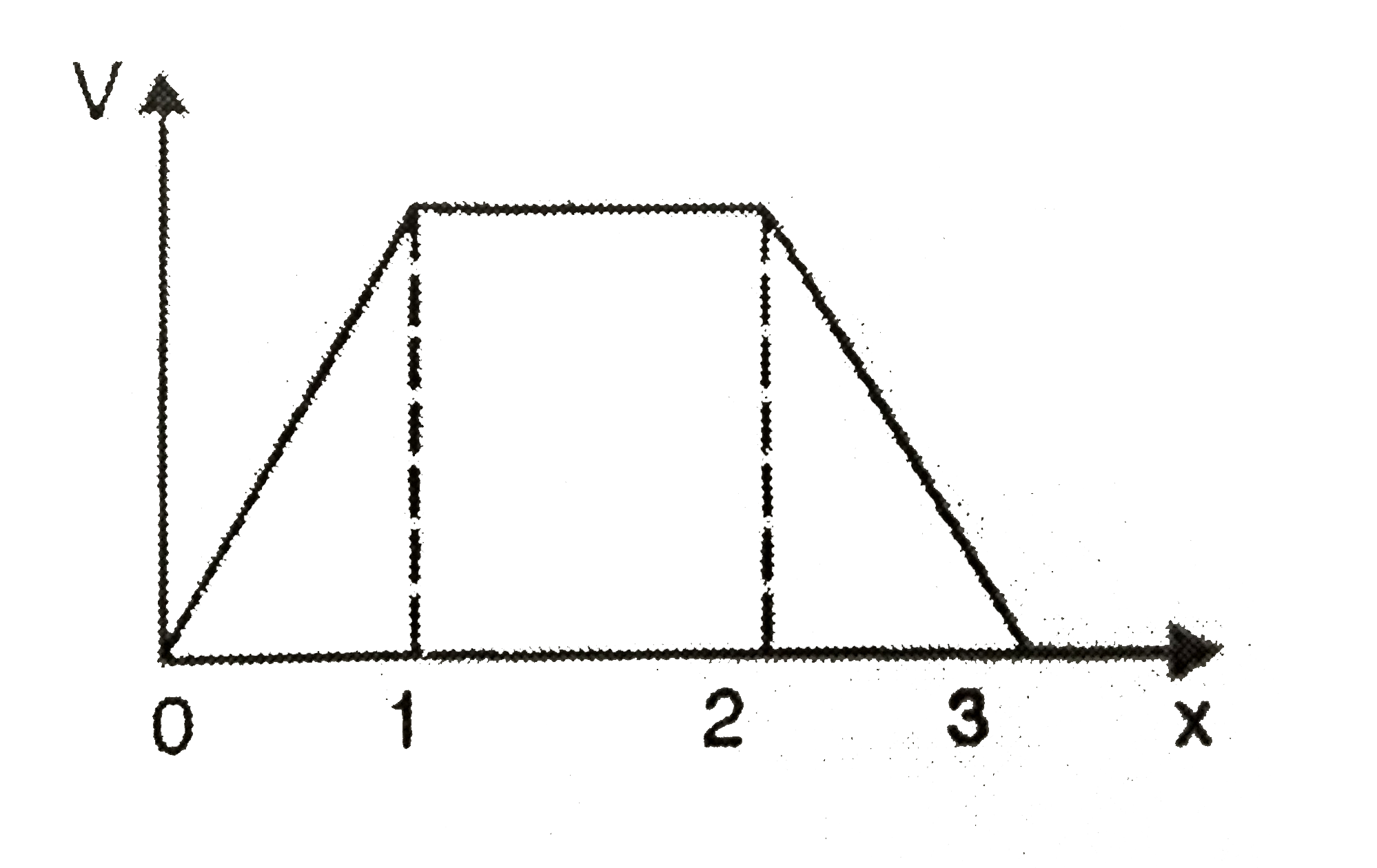
View SolutionA parallel plate capacitor is connected to a battery of emf V volts. Now a slab of dielectric constant k=2 is inserted between the plates of capacitor without disconnecting the battery. The electric field between the plates of capacitor after inserting the slab is E=PV2d. Find the value of P.
View SolutionA parallel - plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected . A slab of dielectric constant K is then inserted between the plate of the capacitor so as to fill the space between the plate .Find the work done on the system in the process of inserting the slab.
View SolutionA parallel-plate capacitor is connected to a cell. Its positive plate A and its negative plate B have charges +Q and −Q respectively. A third plate C, identical to A and B, with charge +Q, is now introduced midway between A and B, parallel to them. Which of the following are correct?
View SolutionEach plate of a parallel plate capacitor has a charge q on it. The capacitor is now connected to a battery. Now,
View Solution
