Question

Conisder a thin spherical shell of radius R with centre at the origin, carrying uniform poistive surface charge denisty. The variation of the magnitude of the electric field $\left|\overrightarrow{E}\left(r\right)\right|$ and the electric potential V(r) with the distance r from the centre, is best represented by which graph?

Options

A.
B.
C.
D.

Explanation

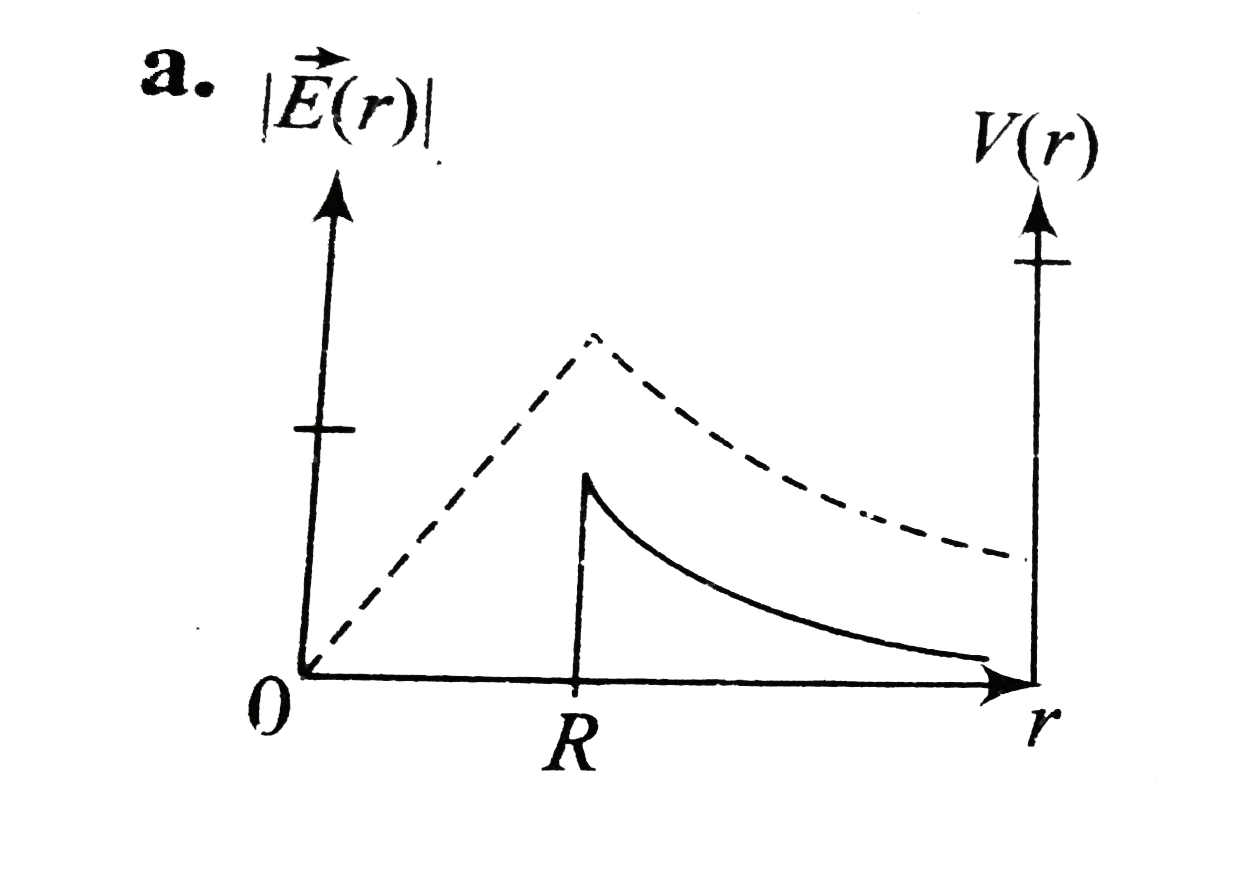
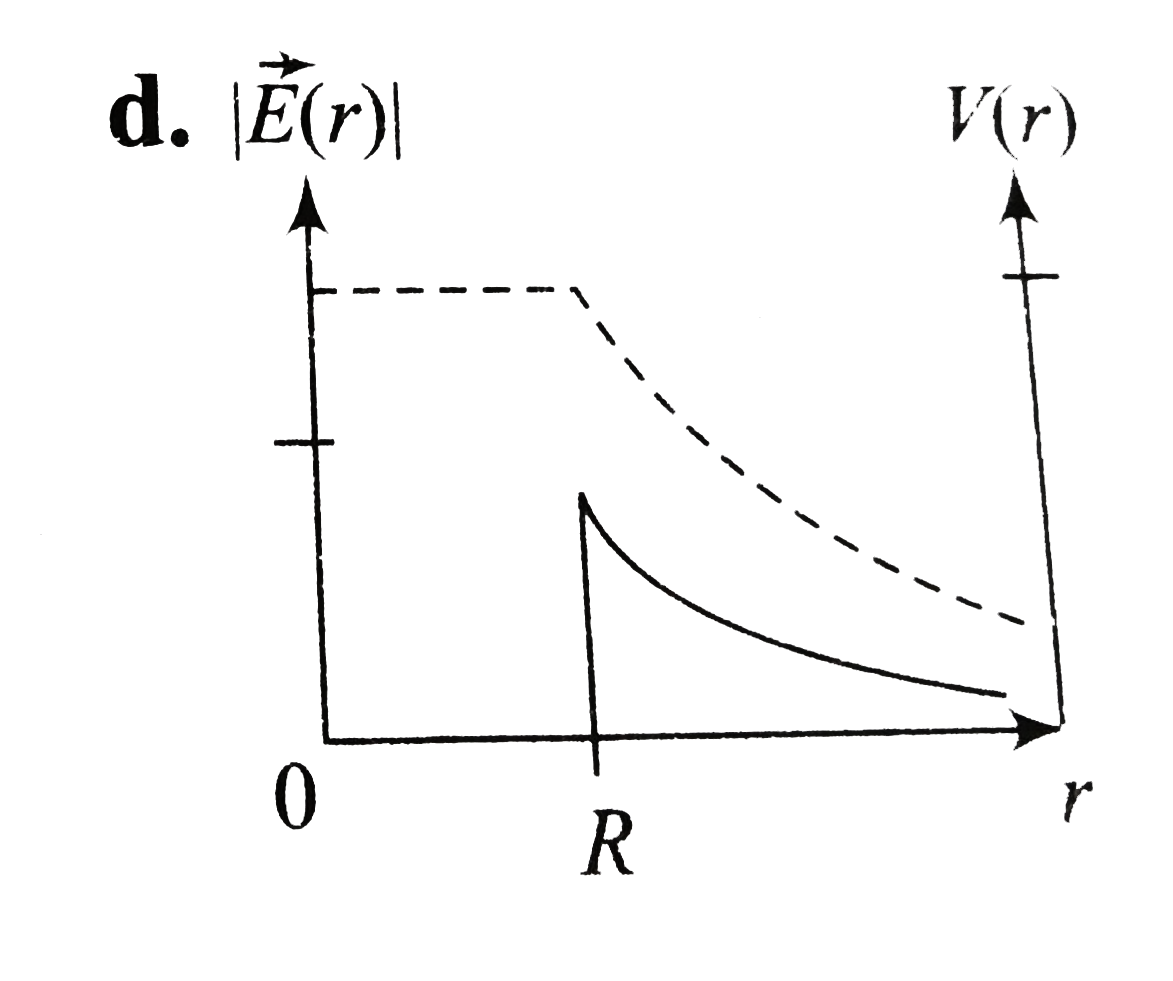
To solve the problem regarding the electric field and electric potential due to a thin spherical shell with uniform positive surface charge density, we will analyze the behavior of both quantities at different distances from the center of the shell.

1. Understanding the System:
We have a thin spherical shell of radius \( R \) with a uniform positive surface charge density. We need to analyze the electric field \( |\vec{E}(r)| \) and the electric potential \( V(r) \) at various distances \( r \) from the center of the shell.

2. Electric Field Inside the Shell:
According to Gauss's law, the electric field inside a uniformly charged spherical shell is zero. Therefore, for \( r < R \):
\( |\vec{E}(r)| = 0 \)

3. Electric Field on the Surface of the Shell:
At the surface of the shell (where \( r = R \)), the electric field can be calculated using the formula:
\( |\vec{E}(R)| = \frac{KQ}{R^2} \)
where \( K \) is Coulomb's constant and \( Q \) is the total charge on the shell.

4. Electric Field Outside the Shell:
For points outside the shell (where \( r > R \)), the electric field behaves as if all the charge were concentrated at the center:
\( |\vec{E}(r)| = \frac{KQ}{r^2} \)

5. Graphing Electric Field:
- For \( r < R \): \( |\vec{E}(r)| = 0 \)
- For \( r = R \): \( |\vec{E}(R)| = \frac{KQ}{R^2} \) (maximum value)
- For \( r > R \): \( |\vec{E}(r)| \) decreases as \( \frac{1}{r^2} \)

The graph of the electric field will be zero for \( r < R \), a maximum at \( r = R \), and will decrease inversely with the square of \( r \) for \( r > R \).

6. Electric Potential Inside the Shell:
The electric potential inside the shell (for \( r < R \)) is constant and equal to the potential at the surface:
\( V(r) = V(R) = \frac{KQ}{R} \)

7. Electric Potential on the Surface of the Shell:
At the surface, the potential is:
\( V(R) = \frac{KQ}{R} \)

8. Electric Potential Outside the Shell:
For \( r > R \), the potential decreases as:
\( V(r) = \frac{KQ}{r} \)

9. Graphing Electric Potential:
- For \( r < R \): \( V(r) = \frac{KQ}{R} \) (constant)
- For \( r = R \): \( V(R) = \frac{KQ}{R} \)
- For \( r > R \): \( V(r) \) decreases as \( \frac{1}{r} \)

The graph of the electric potential will be a horizontal line for \( r < R \), and then it will decrease as \( \frac{1}{r} \) for \( r > R \).

Conclusion
The variation of the electric field and electric potential with distance \( r \) from the center of the shell is best represented by the graphs where:
- The electric field is zero inside the shell, reaches a maximum at the surface, and decreases as \( \frac{1}{r^2} \) outside.
- The electric potential is constant inside the shell and decreases as \( \frac{1}{r} \) outside.