Let V0 be the potential at the origin in an electric field →E=4ˆi+5ˆj. The potential at the point (x,y) is
V0−4x−5y
V0+4x+5y
4x+5y−V0
−4x−5y
The correct Answer is:A
To find the potential at the point (x, y) in the given electric field →E=4^i+5^j, we can follow these steps:
1. Understanding the Electric Field and Potential Relationship:
The relationship between electric field →E and electric potential V is given by:
→E=−∇V
or in differential form:
dV=−→E⋅d→r
2. Identifying the Differential Displacement:
The differential displacement vector d→r from the origin to the point (x, y) can be expressed as:
d→r=dx^i+dy^j
3. Substituting the Electric Field:
Substitute →E into the equation:
dV=−→E⋅d→r=−(4^i+5^j)⋅(dx^i+dy^j)
4. Calculating the Dot Product:
The dot product simplifies to:
dV=−(4dx+5dy)
5. Integrating to Find the Potential:
To find the potential difference from the origin (where the potential is V0) to the point (x, y), we integrate:
V(x,y)−V0=−∫x04dx−∫y05dy
6. Performing the Integrals:
- The integral of 4dx from 0 to x is:
−∫x04dx=−4x
- The integral of 5dy from 0 to y is:
−∫y05dy=−5y
7. Combining the Results:
Combining these results gives:
V(x,y)−V0=−4x−5y
Therefore, we can express V(x,y) as:
V(x,y)=V0−4x−5y
Final Answer:
The potential at the point (x, y) is:
V(x,y)=V0−4x−5y
The relationship between electric field →E and electric potential V is given by:
→E=−∇V
or in differential form:
dV=−→E⋅d→r
The differential displacement vector d→r from the origin to the point (x, y) can be expressed as:
d→r=dx^i+dy^j
Substitute →E into the equation:
dV=−→E⋅d→r=−(4^i+5^j)⋅(dx^i+dy^j)
The dot product simplifies to:
dV=−(4dx+5dy)
To find the potential difference from the origin (where the potential is V0) to the point (x, y), we integrate:
V(x,y)−V0=−∫x04dx−∫y05dy
- The integral of 4dx from 0 to x is:
−∫x04dx=−4x
- The integral of 5dy from 0 to y is:
−∫y05dy=−5y
Combining these results gives:
V(x,y)−V0=−4x−5y
Therefore, we can express V(x,y) as:
V(x,y)=V0−4x−5y
The potential at the point (x, y) is:
V(x,y)=V0−4x−5y
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Let V0 be the potential at the origin in an electric field →E=Exˆi+Eyˆj. The potential at the point (x,y) is
View SolutionA uniform field of 8 N/C exists in space in positive x-direction.
(a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z).
(b) At which points, the potential is 160 V ?
(c) It the potential at the origin is taken to be 80V, what will be the expression for the potential at a general point ?
(d) What will be the potential at the origin if the potential at x = infinity is taken to be zero ?
View Solution(A)Two point charges q1 and q2 are kept r distance apart in a uniform external electric field →E. Find the amount of work done in assembling this system of charges. (B) A cube of side 20 cm is kept in a region as shown in the figure. An electric field →E exists in the region such that the potential at a point is given by V=10x+5, where V is in volt and x is in m. Find the electric field →E and (ii) total electric flux through the cube.

View SolutionElectric dipole of moment →p=pˆi is kept at a point (x,y) in an electric field →E=4xy2ˆi+4x2yˆj. Find the force on the dipole.
View SolutionThe electric potential V(z,y,z) for a planar charge distribution is given by:
V(x,y,z)=⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩0for x<−d−V0(1+xd)2for −d≤x≤0−V0(1+2xd)for 0≤x<d−3V0for x>d
where −V0 is the potential at the origin and d is a distance. Graph of electric field as a function of position is given as
View SolutionAn electric field E=(20ˆi+30ˆj) N/C exists in the space. If the potential at the origin is taken be zero, find the potential at (2m,2m).
View SolutionWhich of the following is a true nut?
View SolutionAn electric field E=(20ˆi+30ˆj) N/C exists in the space. If thepotential at the origin is taken be zero, find the potential at (2m,2m).
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in the figure.
They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V.
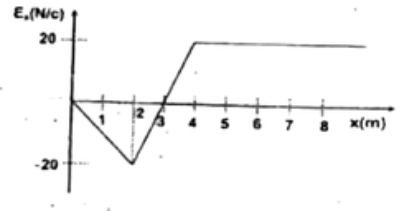
The greatest positive value of electric potential for points of the x-axis for which 0≤x≤6m is
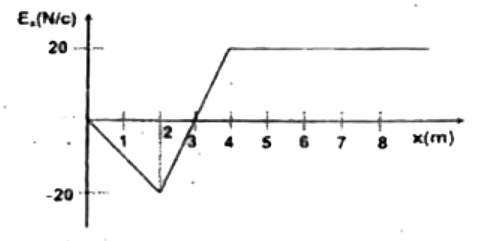
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in the figure. They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V. The value of x for which potential is zero is
View Solution
