A 16μF capacitor , initially charged to 5 V, is started charging at t=0 by a source at the rate of 40tμCs−1. How long will it take to raise its potential to 10 V?
1 s
2 s
3 s
none of these
The correct Answer is:B
To solve the problem, we need to determine how long it will take for a 16 µF capacitor, initially charged to 5V, to reach 10V when charged at a rate of 40µCs.
1. Calculate Initial Charge (Qi):
The initial charge on the capacitor can be calculated using the formula:
\(
Q_i = C \times V_i
\)
Where:
- \( C = 16 \, \mu F = 16 \times 10^{-6} \, F \)
- \( V_i = 5 \, V \)
Substituting the values:
\(
Q_i = 16 \times 10^{-6} \, F \times 5 \, V = 80 \, \mu C
\)
2. Calculate Final Charge (Qf):
The final charge when the capacitor reaches 10V is:
\(
Q_f = C \times V_f
\)
Where:
- \( V_f = 10 \, V \)
Substituting the values:
\(
Q_f = 16 \times 10^{-6} \, F \times 10 \, V = 160 \, \mu C
\)
3. Determine the Change in Charge (ΔQ):
The change in charge required to go from \( Q_i \) to \( Q_f \) is:
\(
\Delta Q = Q_f - Q_i = 160 \, \mu C - 80 \, \mu C = 80 \, \mu C
\)
4. Rate of Charge Flow:
The rate at which the capacitor is charged is given as:
\(
\frac{dQ}{dt} = 40 \, \mu C/s
\)
5. Calculate Time (t):
To find the time required to charge the capacitor from \( Q_i \) to \( Q_f \), we can use the relationship:
\(
\Delta Q = \frac{dQ}{dt} \times t
\)
Rearranging for \( t \):
\(
t = \frac{\Delta Q}{\frac{dQ}{dt}} = \frac{80 \, \mu C}{40 \, \mu C/s} = 2 \, s
\)
Final Answer:
The time required to raise the potential of the capacitor from 5V to 10V is 2 seconds.
---
The initial charge on the capacitor can be calculated using the formula:
\(
Q_i = C \times V_i
\)
Where:
- \( C = 16 \, \mu F = 16 \times 10^{-6} \, F \)
- \( V_i = 5 \, V \)
\(
Q_i = 16 \times 10^{-6} \, F \times 5 \, V = 80 \, \mu C
\)
The final charge when the capacitor reaches 10V is:
\(
Q_f = C \times V_f
\)
Where:
- \( V_f = 10 \, V \)
\(
Q_f = 16 \times 10^{-6} \, F \times 10 \, V = 160 \, \mu C
\)
The change in charge required to go from \( Q_i \) to \( Q_f \) is:
\(
\Delta Q = Q_f - Q_i = 160 \, \mu C - 80 \, \mu C = 80 \, \mu C
\)
The rate at which the capacitor is charged is given as:
\(
\frac{dQ}{dt} = 40 \, \mu C/s
\)
To find the time required to charge the capacitor from \( Q_i \) to \( Q_f \), we can use the relationship:
\(
\Delta Q = \frac{dQ}{dt} \times t
\)
Rearranging for \( t \):
\(
t = \frac{\Delta Q}{\frac{dQ}{dt}} = \frac{80 \, \mu C}{40 \, \mu C/s} = 2 \, s
\)
The time required to raise the potential of the capacitor from 5V to 10V is 2 seconds.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Capacitance of a conductor is 1μF. What charge is required to raise its potential to 100V?
View SolutionA 2μF capacitor is charged to 100V, and then its plates are connected by a conducting Wire. The heat produced is .
View SolutionA capacitor charged to 50V is discharged by connecting the two plates at t=0.If the potential difference across the plates drops to 1.0 V at t=10 ms,what will be the potential difference at t=20 ms?
View SolutionA 1.5μF capacitor is charged to 20 V. The charging battery is then disconnected , and a 15 mH coil is connected in series with the capacitor so that LC oscillations occur. Write the equation for variation of charge on capacitor and current in the inductor with time taking the instant at which inductor is connected to the capacitor as t=0.
View SolutionA 1.5μf capacitor is charged to 20 V. The charging battery is then disconnected and a 15 mH coil is connected in series with the capacitance so that LC oscillations occur. Write the equation for variation of charge on capacitor and current in the inductor with time taking at the instant at which inductor is connected to the capacitor at t = 0
View SolutionA capacitor of 20μF charged upto 500 V is connected in parallel with another capacitor of 10μF, which is charged upto 200 V. the common potential is
View SolutionA radioactive source, in the form of a metallic sphere of radius 10−2m emits β−particles at the rate of 5×1010 particles per second. The source is electrically insulated. How long will it take for its potential to be raised by 2V, assuming that 40% of the emitted β−particles escape the source.
View SolutionA capacitorn of 2μF charged to 50 V is connected in parallel with another capacitor of 1μF charged to 20 V. The common potential and loss of energy will be
View SolutionA 10μF capacitor is charged to 15V. It is next connected in seties with an uncharged 5μf capacitor. The series cambination is finally connected across a 30V battery, as shown in. Find the new potential differnce across the 5μF and 10μF capacitors.
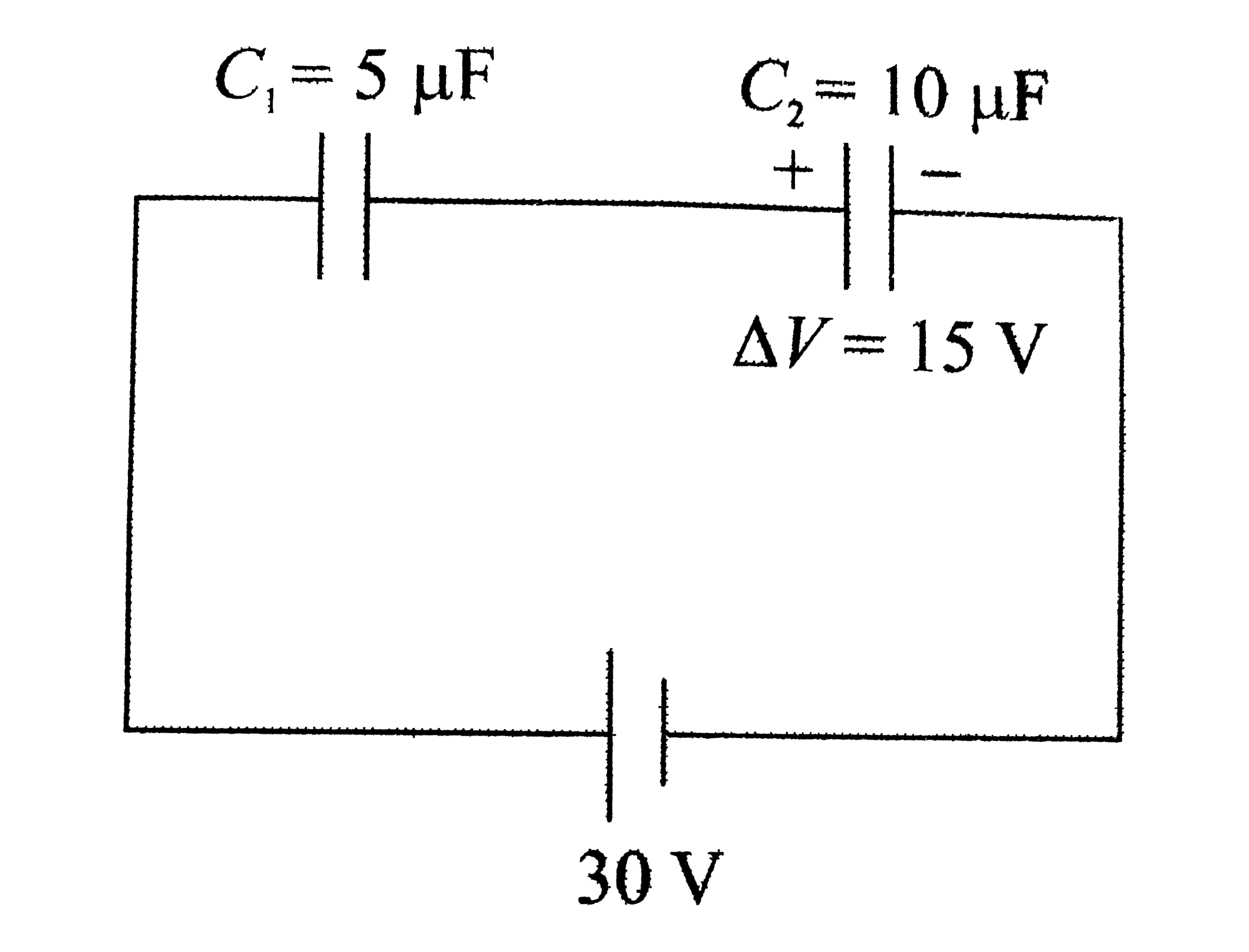
View SolutionA 8uF capacitor C1 is charged to V0=120V. The charging battery is then removed and the capacitor is connected in parallel to an uncharged +4μF capacitor C2.
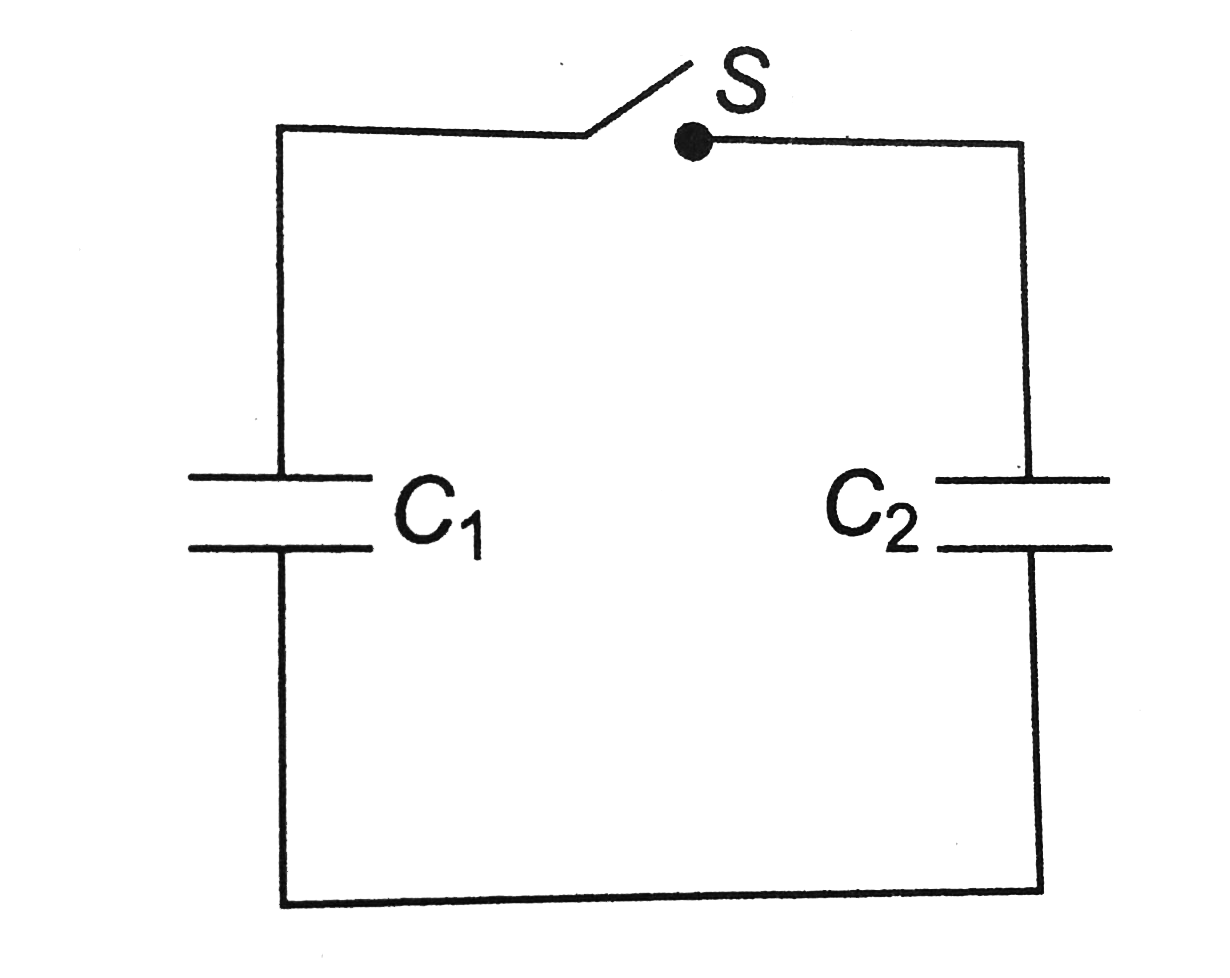
(a) what is the potential difference V across the combination?
(b) what is the stored energy before and after the switch S is closed?
View Solution
