An ammetre is obtained by shunting a 30Ω galvanometer with a 30Ω resistance. What additional shunt should be connected across it to double the range ?
15Ω
10Ω
5Ω
none of these
The correct Answer is:A
To solve the problem, we need to determine the additional shunt resistance required to double the range of an ammeter that is already shunted with a 30-ohm galvanometer and a 30-ohm shunt resistance.
1. Identify Given Values:
- Resistance of galvanometer, RG=30Ω
- Initial shunt resistance, S=30Ω
2. Understand the Current Relationships:
- Let I be the total current through the ammeter.
- The current through the galvanometer is IG.
- The current through the shunt is I−IG.
3. Apply the Voltage Equality:
- The voltage across the galvanometer and the shunt must be equal:
IG⋅RG=(I−IG)⋅S
- Substituting the known values:
IG⋅30=(I−IG)⋅30
- Simplifying this gives:
IG=I−IG⟹2IG=I⟹I=2IG
4. Determine New Current for Doubling the Range:
- To double the range of the ammeter, the new total current I′ should be:
I′=2I=2(2IG)=4IG
5. Set Up the New Voltage Equality:
- For the new situation with the new shunt resistance S′:
IG⋅RG=(I′−IG)⋅S′
- Substituting I′=4IG:
IG⋅30=(4IG−IG)⋅S′⟹30IG=3IG⋅S′
- Dividing both sides by IG (assuming IG≠0):
30=3S′⟹S′=10Ω
6. Calculate the Additional Shunt Resistance:
- The initial shunt resistance S=30Ω and the new required shunt resistance S′=10Ω.
- The additional shunt resistance X can be found using the formula for resistances in parallel:
1X=1S′−1S
- Substituting the values:
1X=110−130
- Finding a common denominator (30):
1X=330−130=230=115
- Therefore, X=15Ω.
Final Answer:
The additional shunt resistance that should be connected across the galvanometer to double the range is 15Ω.
- Resistance of galvanometer, RG=30Ω
- Initial shunt resistance, S=30Ω
- Let I be the total current through the ammeter.
- The current through the galvanometer is IG.
- The current through the shunt is I−IG.
- The voltage across the galvanometer and the shunt must be equal:
IG⋅RG=(I−IG)⋅S
- Substituting the known values:
IG⋅30=(I−IG)⋅30
- Simplifying this gives:
IG=I−IG⟹2IG=I⟹I=2IG
- To double the range of the ammeter, the new total current I′ should be:
I′=2I=2(2IG)=4IG
- For the new situation with the new shunt resistance S′:
IG⋅RG=(I′−IG)⋅S′
- Substituting I′=4IG:
IG⋅30=(4IG−IG)⋅S′⟹30IG=3IG⋅S′
- Dividing both sides by IG (assuming IG≠0):
30=3S′⟹S′=10Ω
- The initial shunt resistance S=30Ω and the new required shunt resistance S′=10Ω.
- The additional shunt resistance X can be found using the formula for resistances in parallel:
1X=1S′−1S
- Substituting the values:
1X=110−130
- Finding a common denominator (30):
1X=330−130=230=115
- Therefore, X=15Ω.
The additional shunt resistance that should be connected across the galvanometer to double the range is 15Ω.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Multiple Correct7videos
ELECTRICAL MEASURING INSTRUMENTS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Assertion-Reasoning7videos
ELECTRICAL MEASURING INSTRUMENTS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Subjective18videos
ELECTRICAL MEASURING INSTRUMENTS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.515videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - compression type7videos
ELECTROMAGNETIC INDUCTION
Similar Questions
The resistance of an ammeter is 13Ω and its scale is graduated for a current upto 100A. After an additional shunt has been connected to this ammeter it becomes possible to measure currents upto 750A by this meter. The value of shunt resistance is
View SolutionA galvanometer of resistance 22.8Ω measures 1 A. How much shunt should be used , so that it can be used to measure 20 A ?
View Solution(a) Briefly explain how a galvanometer is converted into a voltmeter.
(b) A voltmeter of a certain range is constructed by connecting a resistance of 980Ω in series with a galvanometer. When the resistance of 470Ω is connected in series, the range gets halved. Find the resistance of the galvanometer.View SolutionA moving coil galvanometer of resistance 20Ω gives a full scale deflection when a current of 1mA is passed through it. It is to be converted into an ammeter reading 20A on full scale. But the shunt of 0.005Ω only is available. What resistance should be connected in series with the galvanometer coil?
View SolutionA moving coil galvanometer of resistance 20Ω gives a full scale deflection when a current of 1mA is passed through it. It is to be converted into an ammeter reading 20A on full scale. But the shunt of 0.005Ω only is available. What resistance should be connected in series with the galvanometer coil?
View SolutionIn an experiment with a potentiometer, the null point is
obtained at a distance of 60cm along the wire from the
common terminal with a leclanche cell. When a shunt
resistance of 1Ω is connected across the cell, the null
point shifts to a distance of 30cm from the common
terminal. what is the internal resistance of the cell?View SolutionIf a current of 0.5 apere flows through a metallic wire for 2 hour then how many electrons flow through the wire ?
View SolutionA galvanometer of resistance 20Ω is shunted by a 2Ω resistor. What part of the main current flows through the galvanometer ?
View SolutionIn the circuit shown, reading of the voltmeter connected across 400Ω resistance is 60 V. If it is connected across 300Ω resistance then reading in volt will be
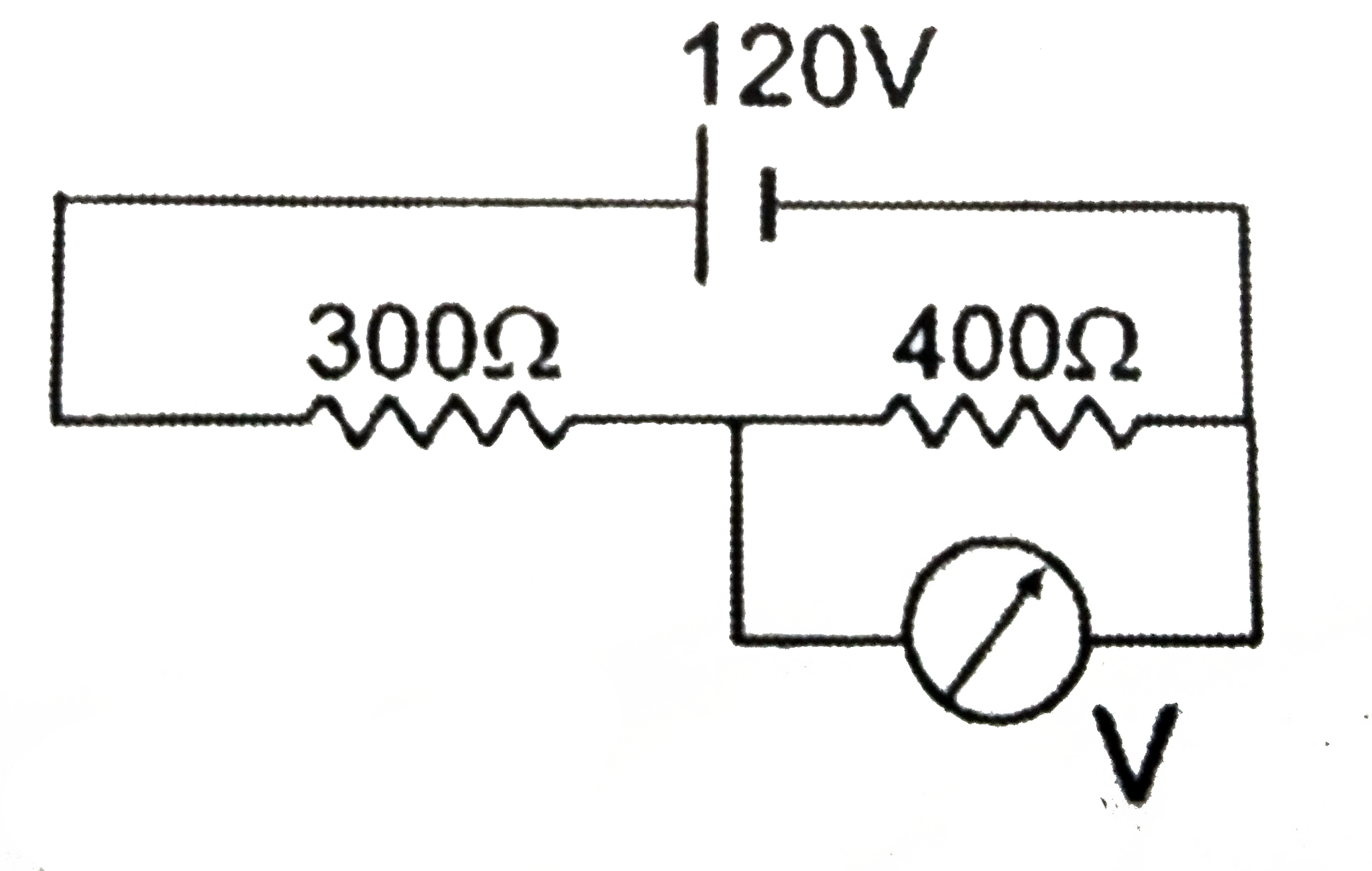 View Solution
View SolutionThe deflection in galvanometer falls to (14)th when it is shunted by 3Ω. If additional shunt of 2Ωis connected to earlier shunt in parallel, the deflection in galvanometer falls to
View Solution
