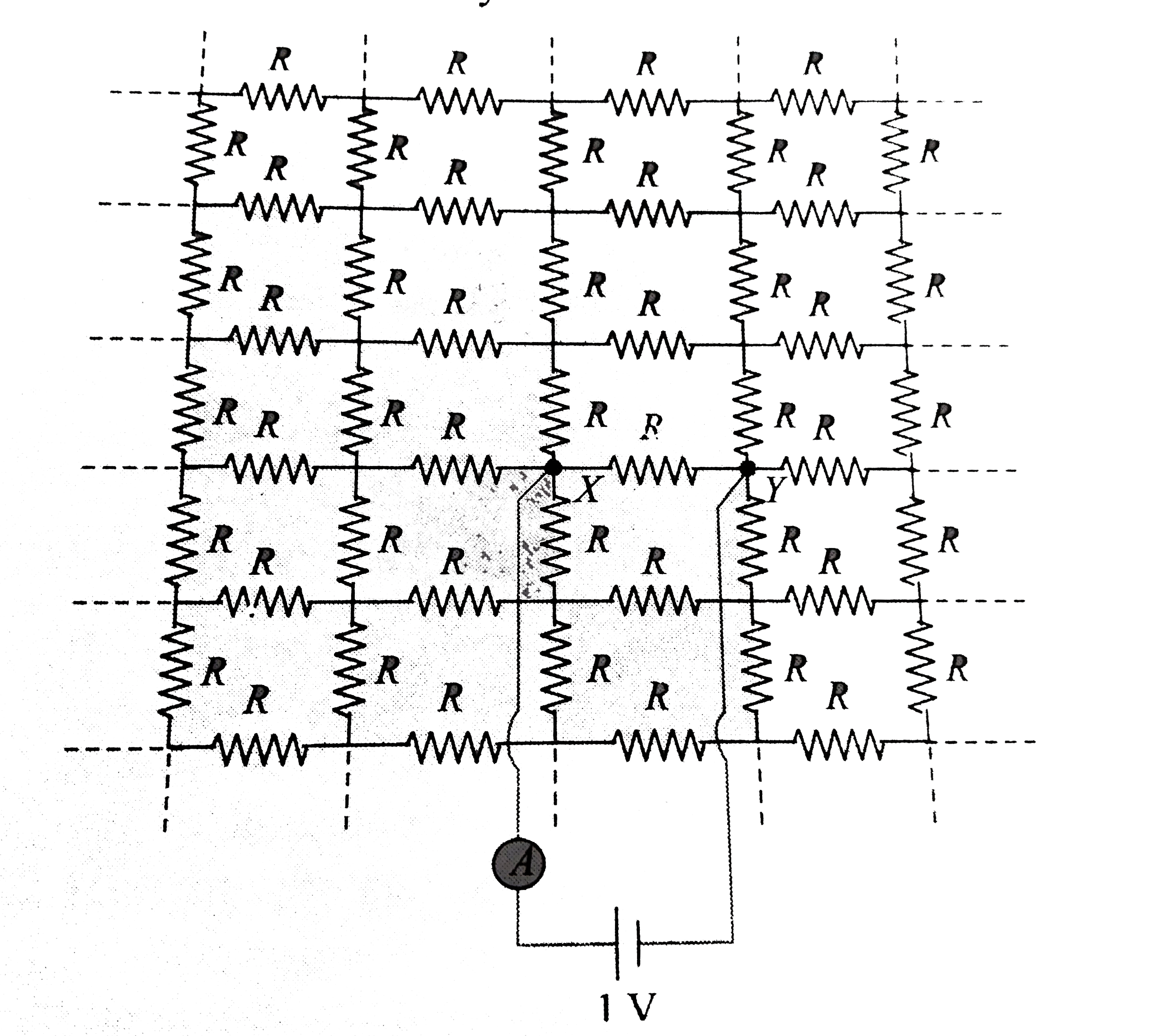
Each component in the infinite network shwon in fig has a resistance R=4Ω. A battery of emf1 V and neglibible interanal resistance is connected between any two neighboring points, say X and Y.
i. Find current shown by the ammeter.
ii. if the resistance R between X and Y is removed , then find current shown by ammeter.
understanding of symmetry and superposiiton could
greatly help in solving the given cirucit. A battery is connected
between any tow neighboring points x and Y . Consider first
the distribution of curent at X as shown in fig. (a). A
current I enters the cirucit at X and distributes in the infinite network. by symmetry, the current will be divided equally
in the four resistance conneced to X. this is beacues of the mutual equivalent of sthe four possible direciton in which the current distributes at X.
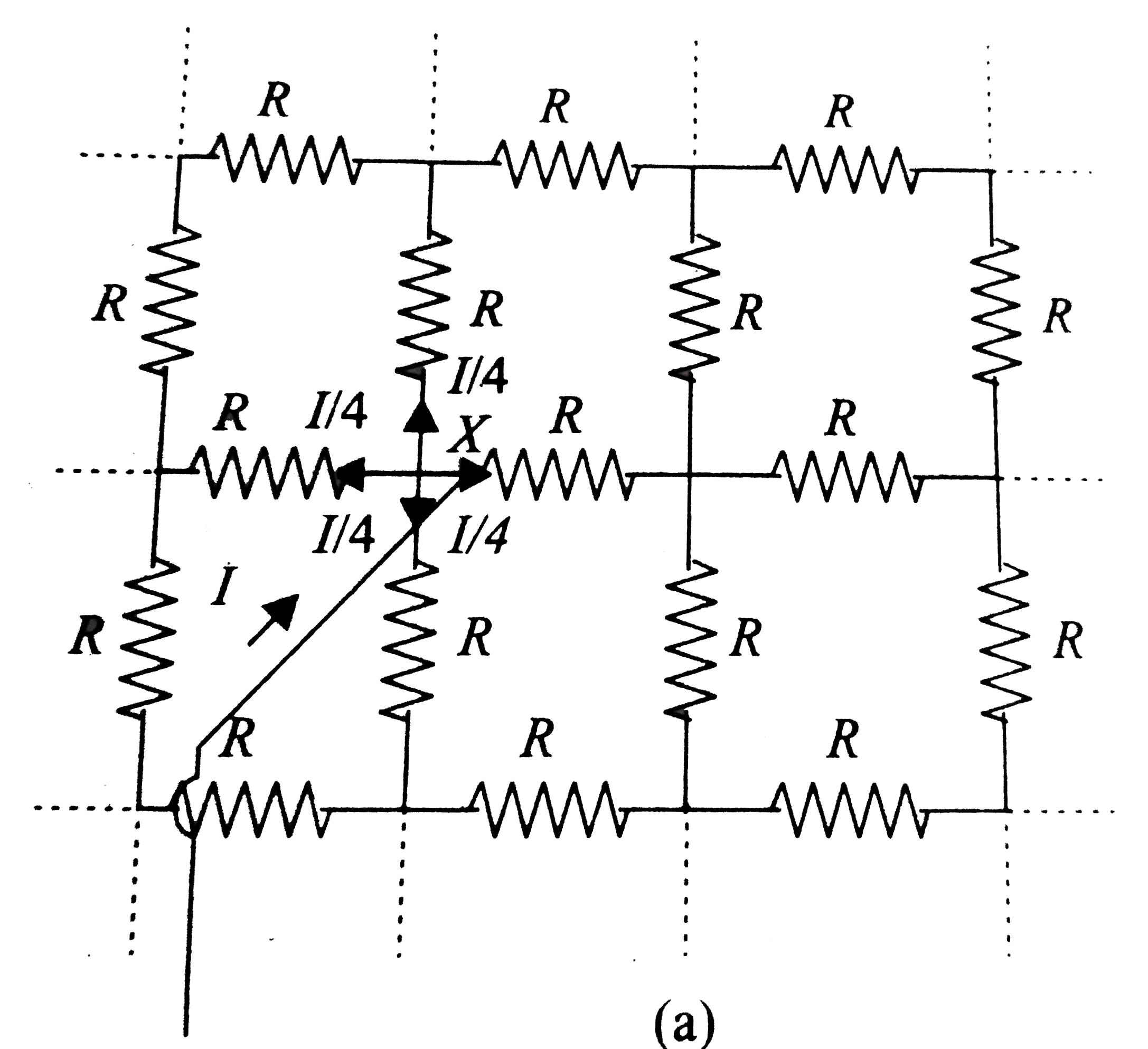

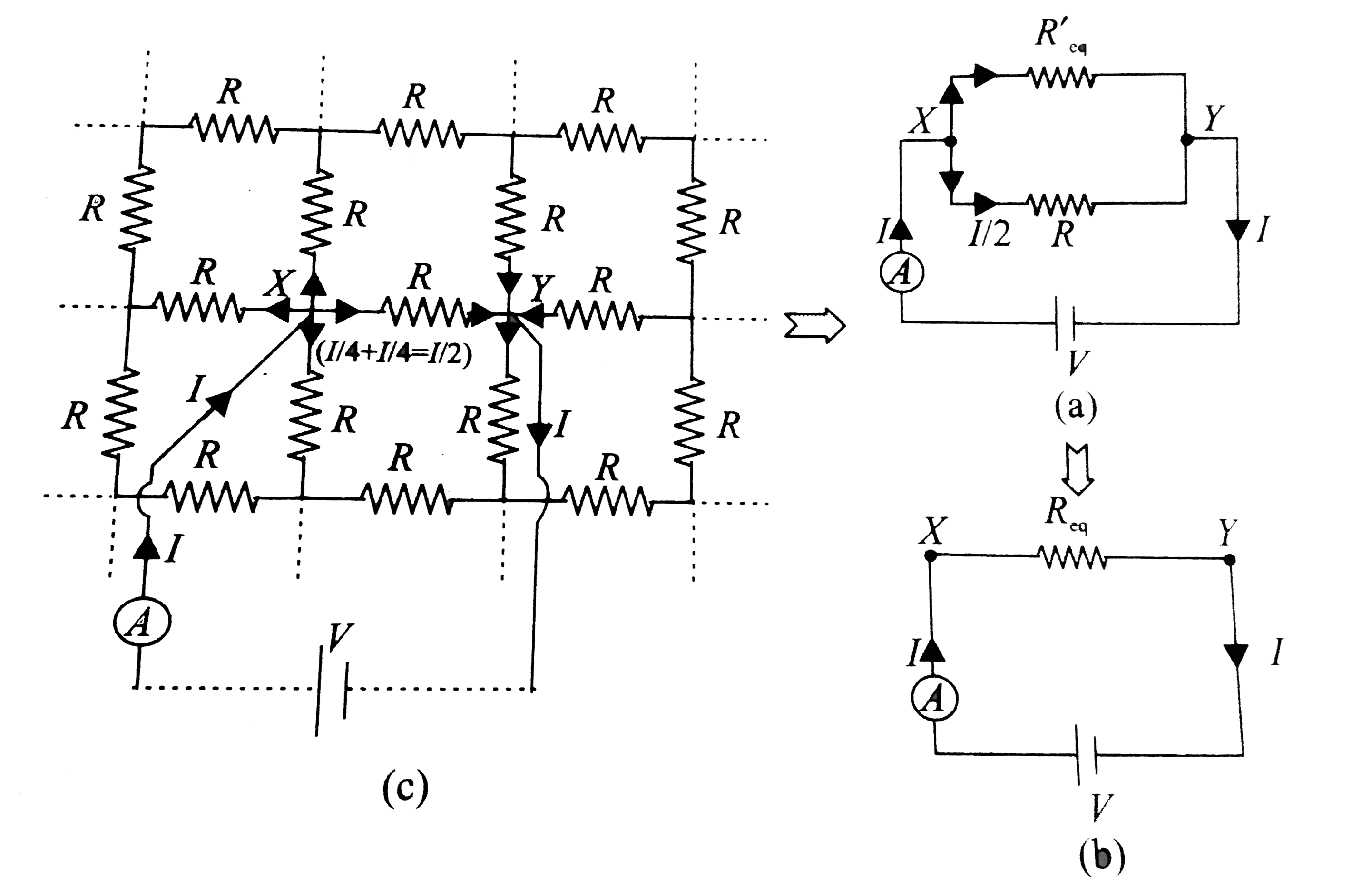
Now consider the neighboring point Y, which is connected
to the negative terminal of the battery. By symmetry and
independence of our earlier discussion, if a current I has to
leave the circuit at Y, current each I/4 will be directed toward
B through the four resistors connected to Y, as shown in fig
Let us now superpose the two cases so that a current I enters
at X and leaves at Y. Superposition of figs. is shown
fin in the resistance R between X and Y, the two currents in figs (b) being in the same direction, add
up and a total current I/2 ,passes through it. Thus, current I divides at X such that I/2 goes through this R and the remaining
I/2 through the rest of circuit, and at Y, these currents are
combined resulting in current I leaving the network.
It implies that we can cosider the network to consist of
two resistance connected in parallel between X and Y. One
of these is the resistane R between X and Y and the other is
the equivalent resistance of the rest of cirucit. This shown in fig.
 ,
,
From fig (a) we have V=12R
and from (b) we have V=IReq
IReq=I2RorReq=R2
Hence, the equivalent resistance resistance fo the network between X and
Y or any two neighboring points si R/2
V=IReq,I=VReq
Req=R2,I=2VR
Given V=1VandR=4Ω
I=24=0.5A
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.128videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.250videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
A battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionIn the network shown in fig. each resistance is R.

The equivalent resistance between A and C isView SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.
 View Solution
View SolutionEach resistor shown in the figure has a resistance of 10Ω and the battery has the emf 6 V. What will be the current supplied by the battery ?
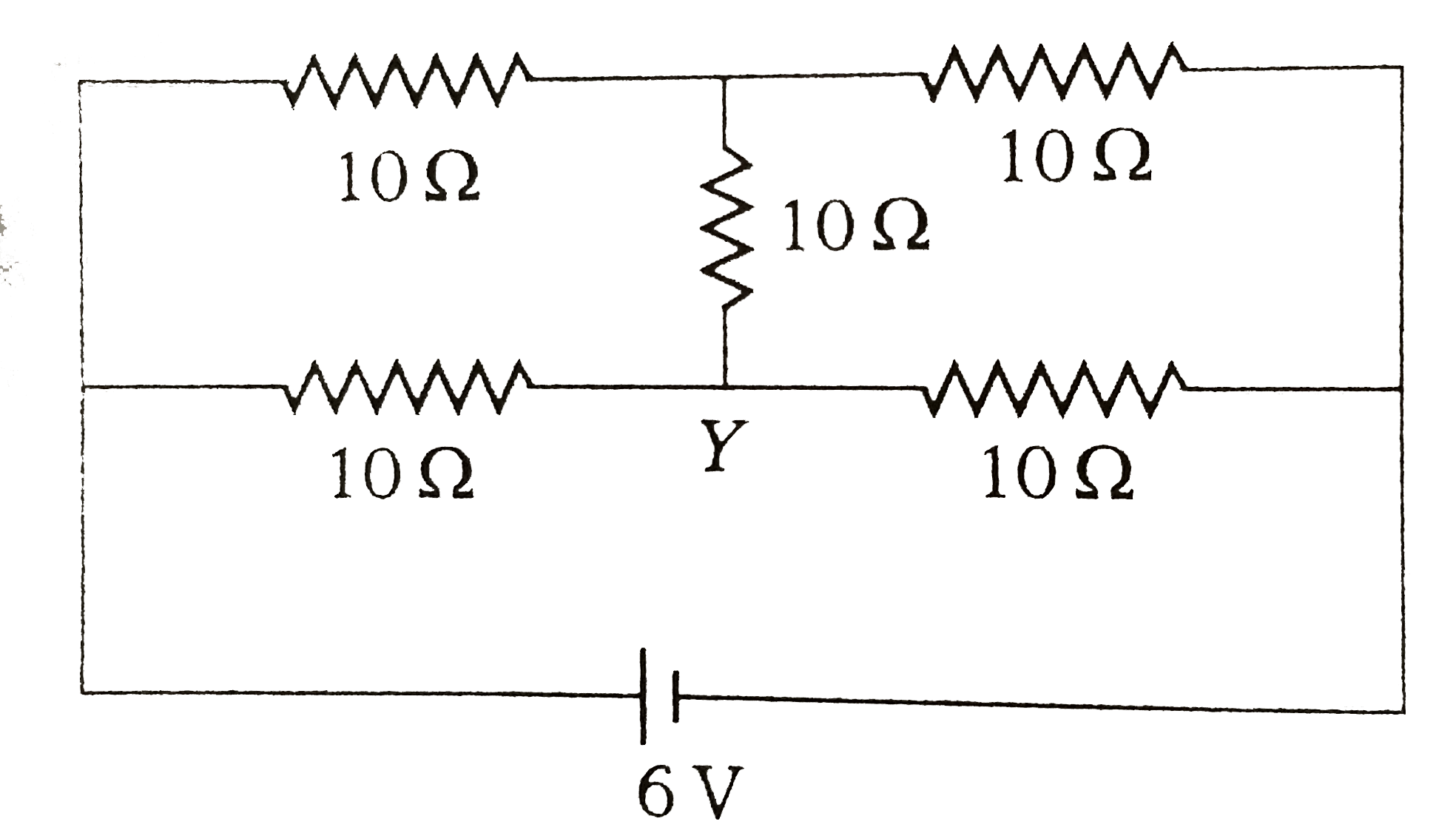 View Solution
View SolutionA 10 V battery of negilgible internal resistance is connected across a 200V battery and a resistance of 38Ω as shown in figure.
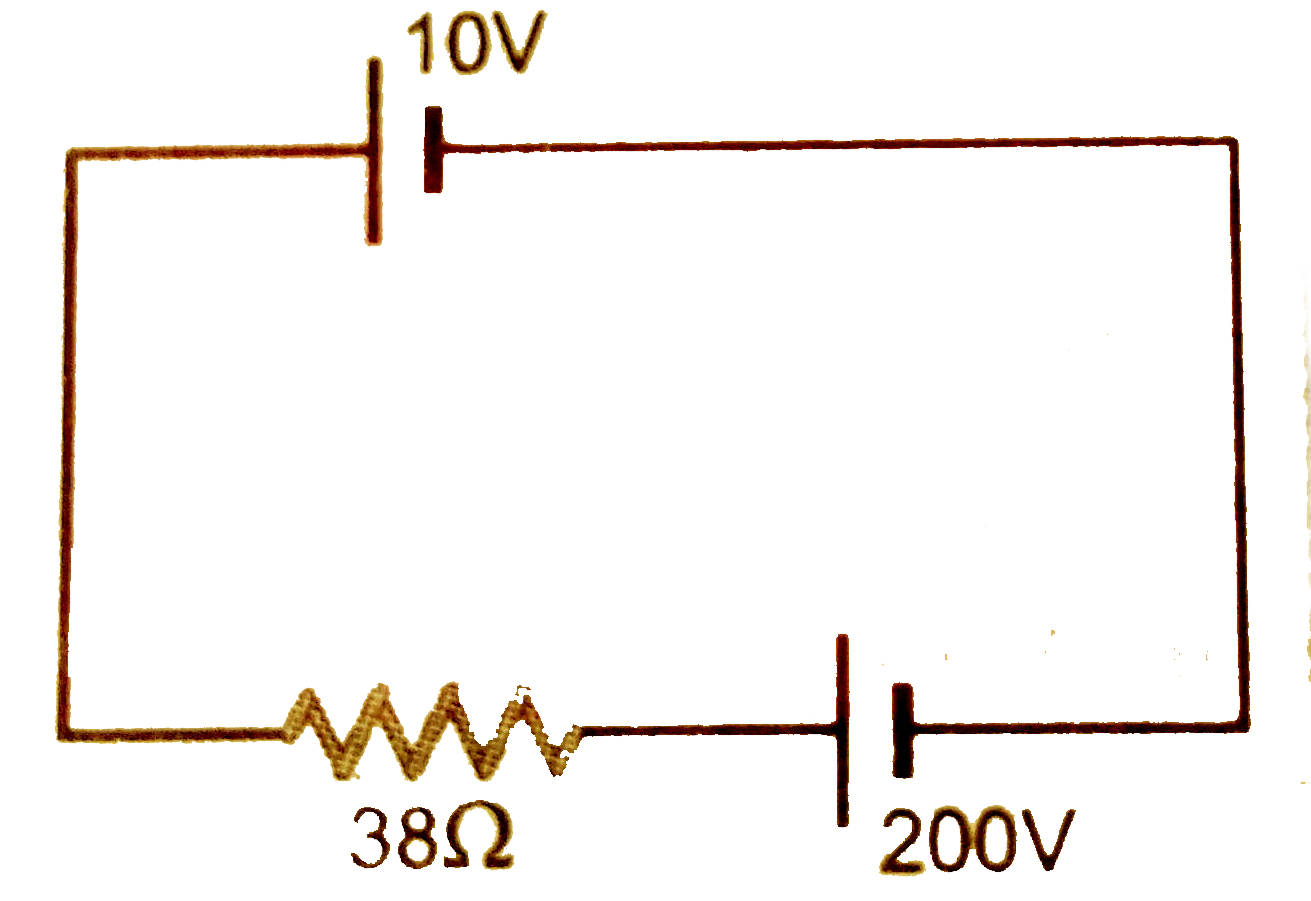 . Find the value of current in the circuit.View Solution
. Find the value of current in the circuit.View SolutionEach of the resistor shown in fig. has resistance R. Find the equivalent resistance between A and B
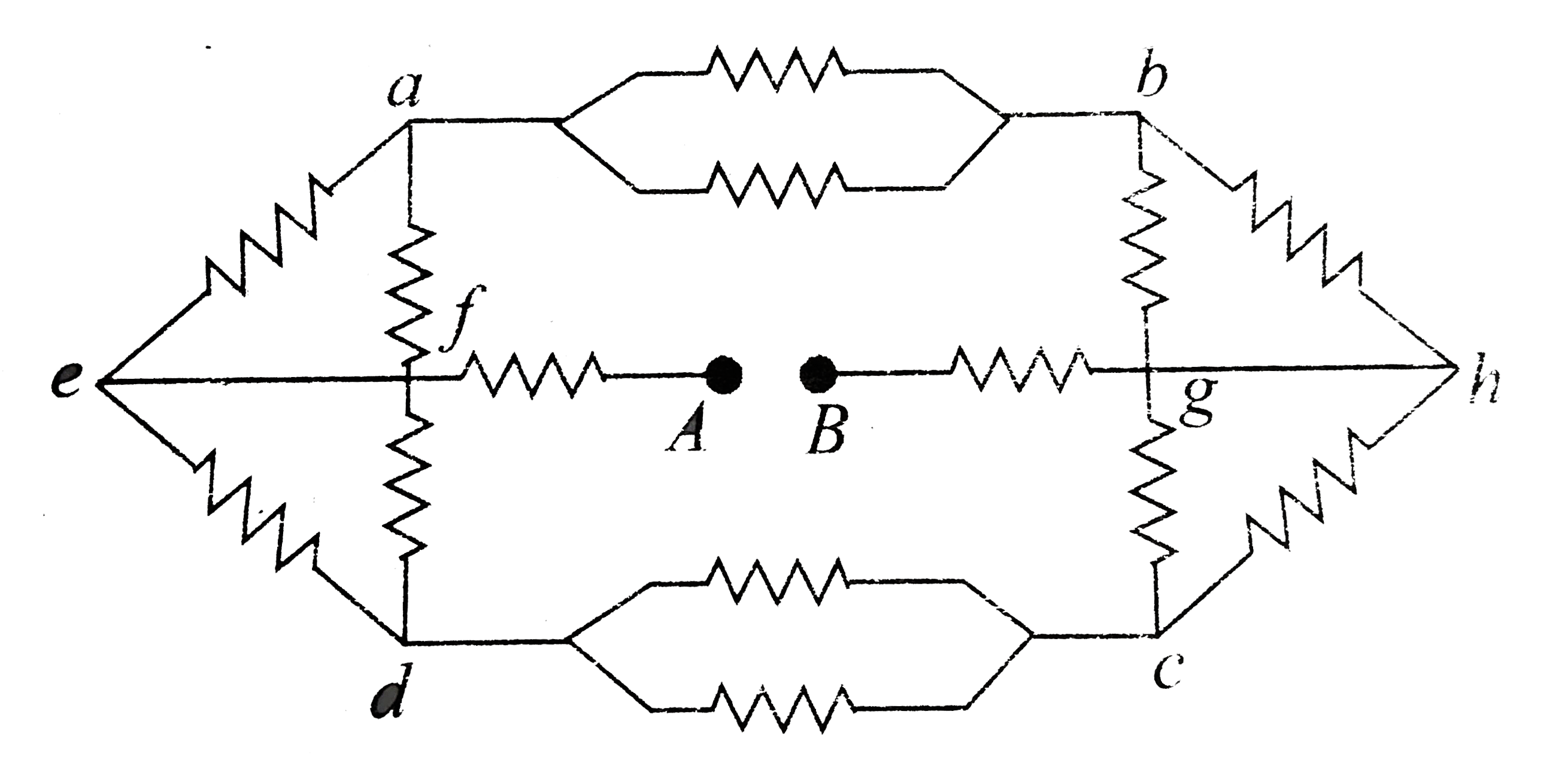 View Solution
View SolutionFind the current drawn from a cell of emf 2 V and internal resistance 2Ω connected to the network given below.
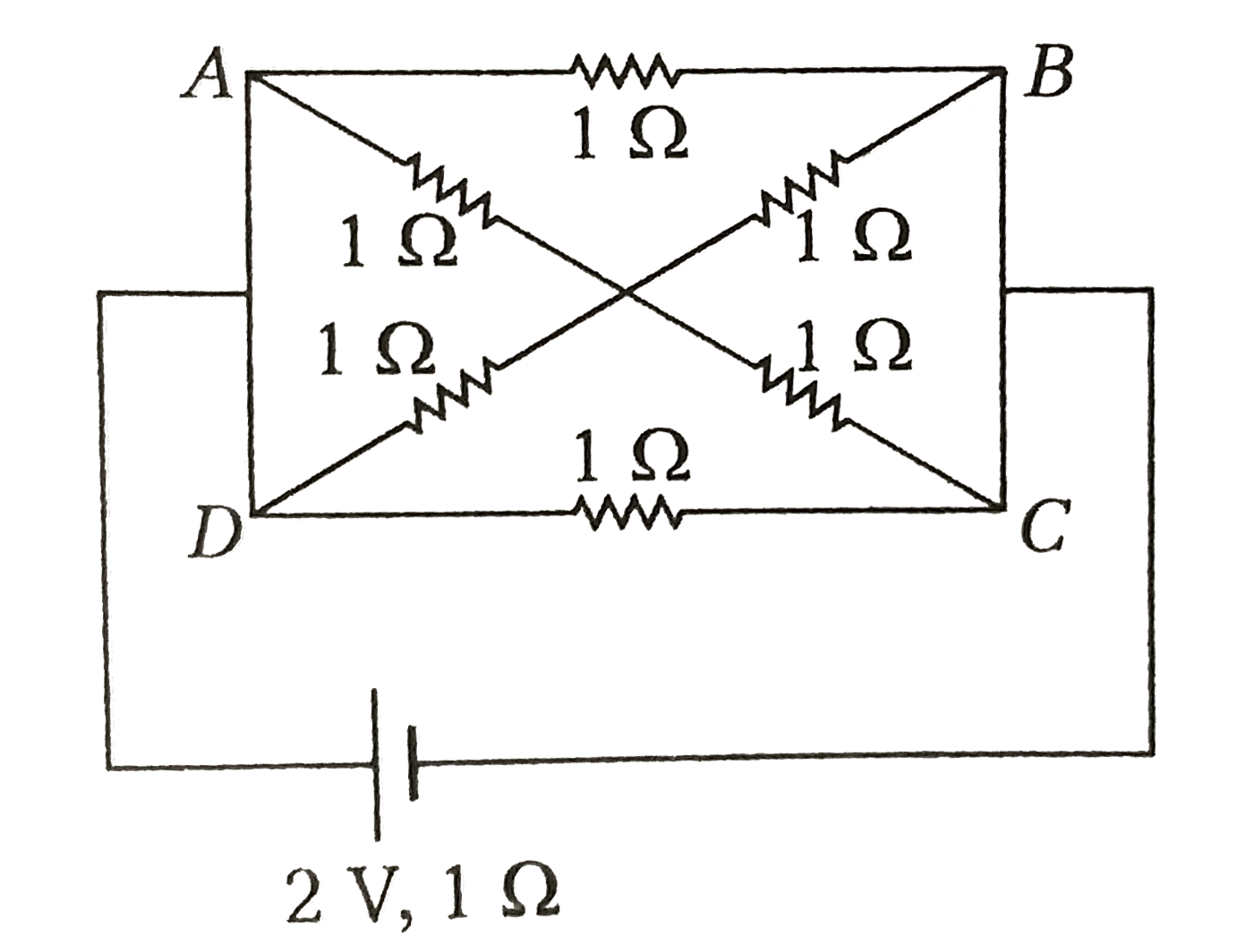 View Solution
View SolutionIn the network shown in figure, each resistance is R. The equvalent resistance between points A and B is
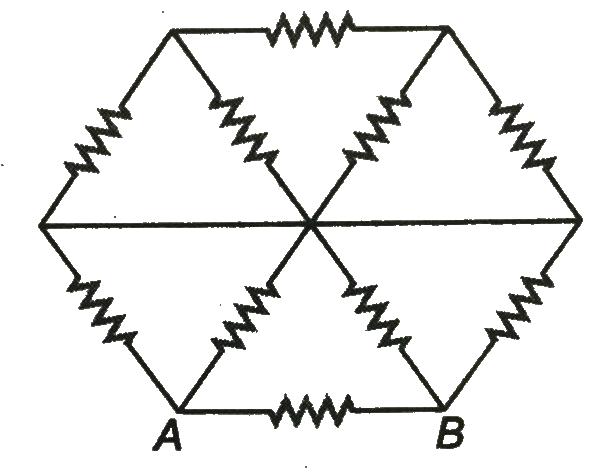 View Solution
View SolutionIn a given network, each resistance has value of 6Ω . The point X is connected to point A by a copper wire of negligible resistance and point Y is connected to point B by the same wire. The effective resistance between X and Y will be
 View Solution
View SolutionTwo batteries one of the emf 3V, internal resistance 1Ω and the other of emf 15V, internal resistance 2Ω are connected in series with a resistance R as shown. If the potential difference between points a and b is zero, the resistance R in Ω is
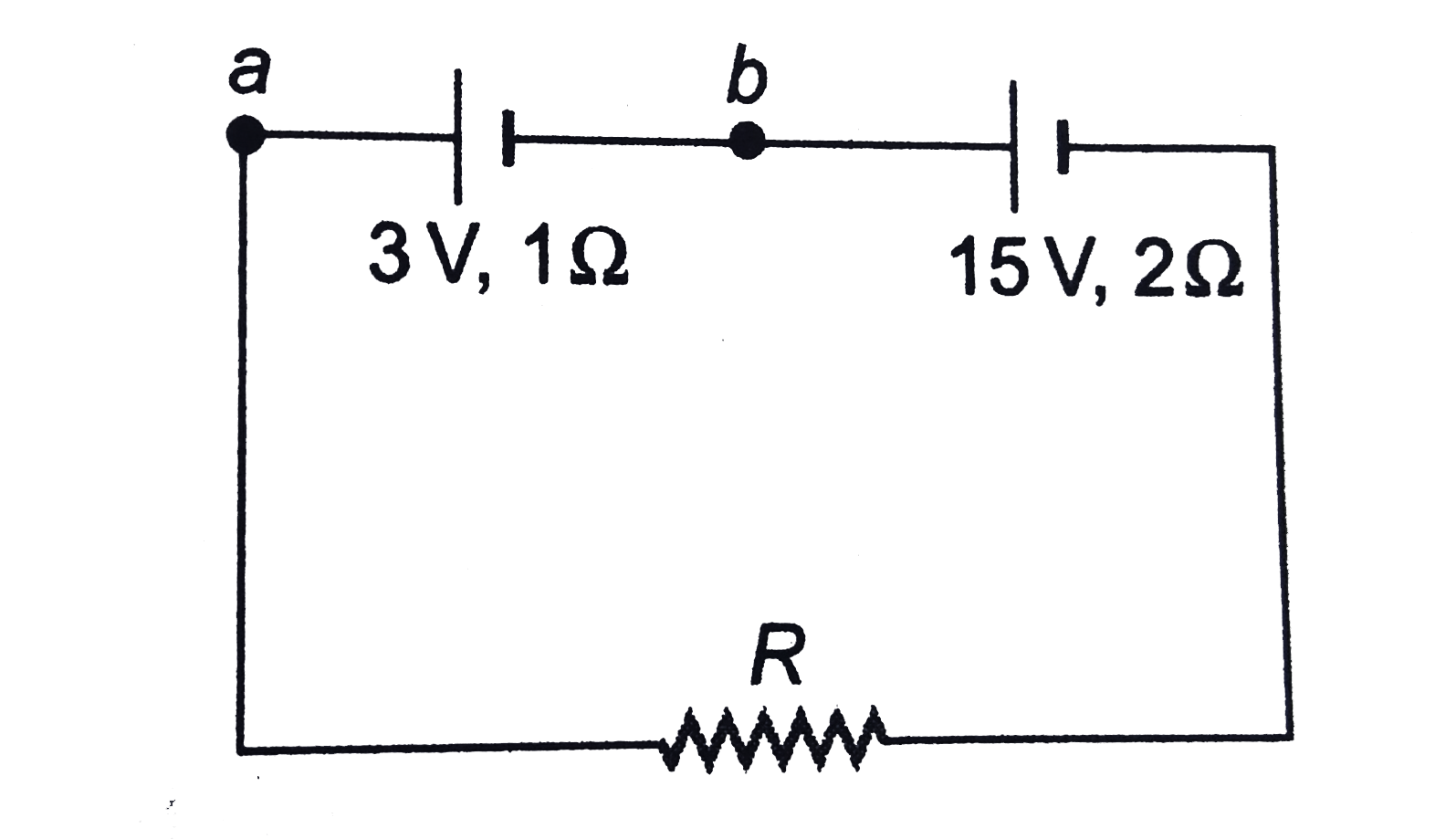 View Solution
View Solution
