The capacitor shown in figure has been charged to a potential difference of V volt, so that it carries a charge CV with both the switches S1andS2 remaining open. Switch S1 is closed at t=0. At t=R1C switch S1 is opened and S2 is closed. Find the charge on the capacitor at t=2R−1C+R2C.
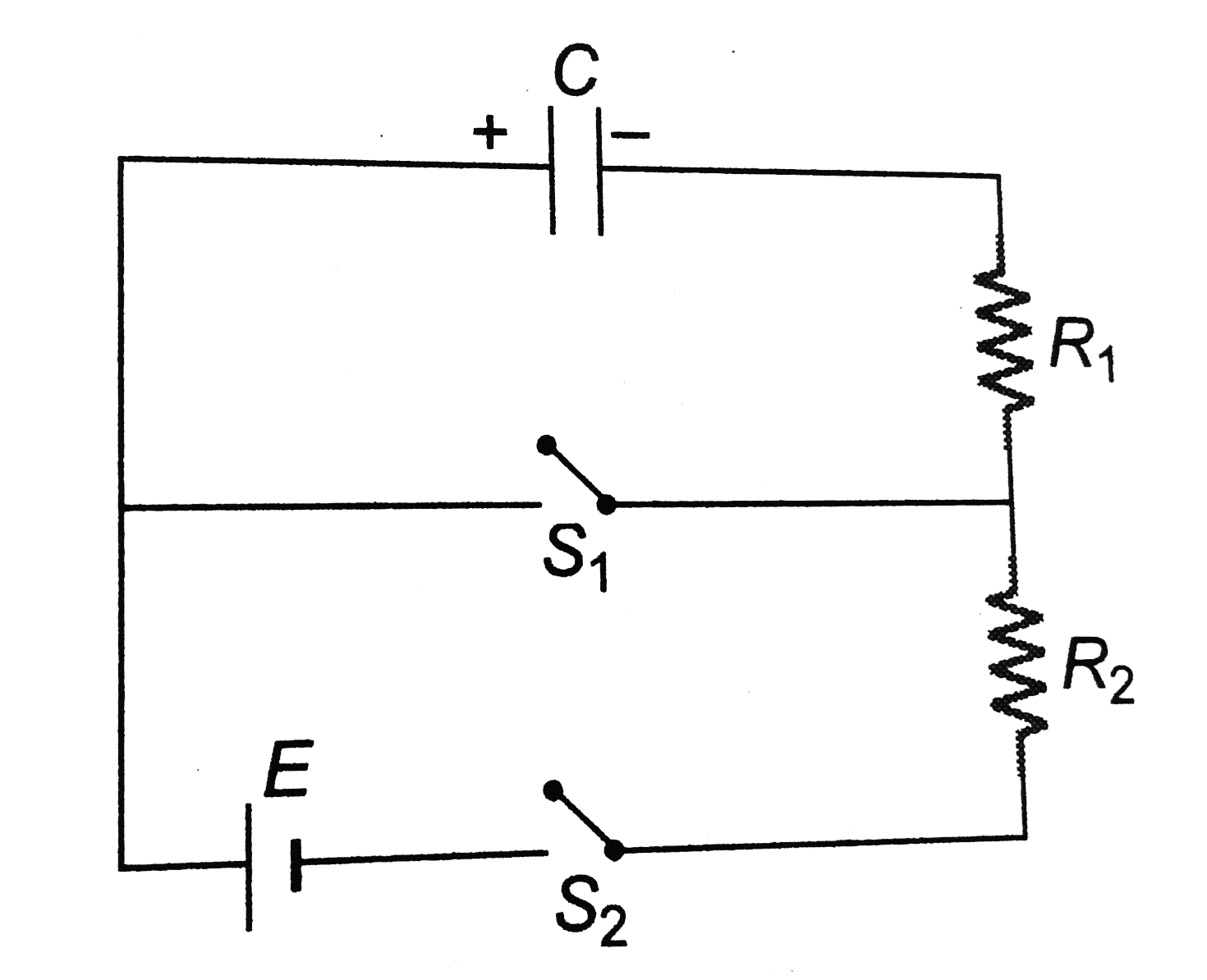
First, capacitor will discharge through R−1.
At t=R1C,q1=CV(e−R1C/R1C)=CVe
Now it will be charged through R1+R2. so
∫qq1dqCε−q=∫2R1C+R2CR1Cdt(R1+R2)C
or q=Cε(1−1e)+CVe2

When the switch S1 is opened and S2 is closed, the capacitor
is finally chaged ot qf∈al=Cε. Hence, capacitor is charged from q0toqf exponentially. in this case, the time after S2 is closed is
Δt=(2R1C+R2C)−R1C)−R1C=(R1C+R2C)=(R1+R2)C
The time constant of the circuit after switch S2 is closed is
τ=(R1+R2)C
Hence, required value of charge si
q=CVE+(Cε−CVe)(1−e−(R1+R2)C(R1+R2)C)
=CVe+(Cε−CVe)(1−e−1)=Cε(1−1e)+CVe2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples12videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.128videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
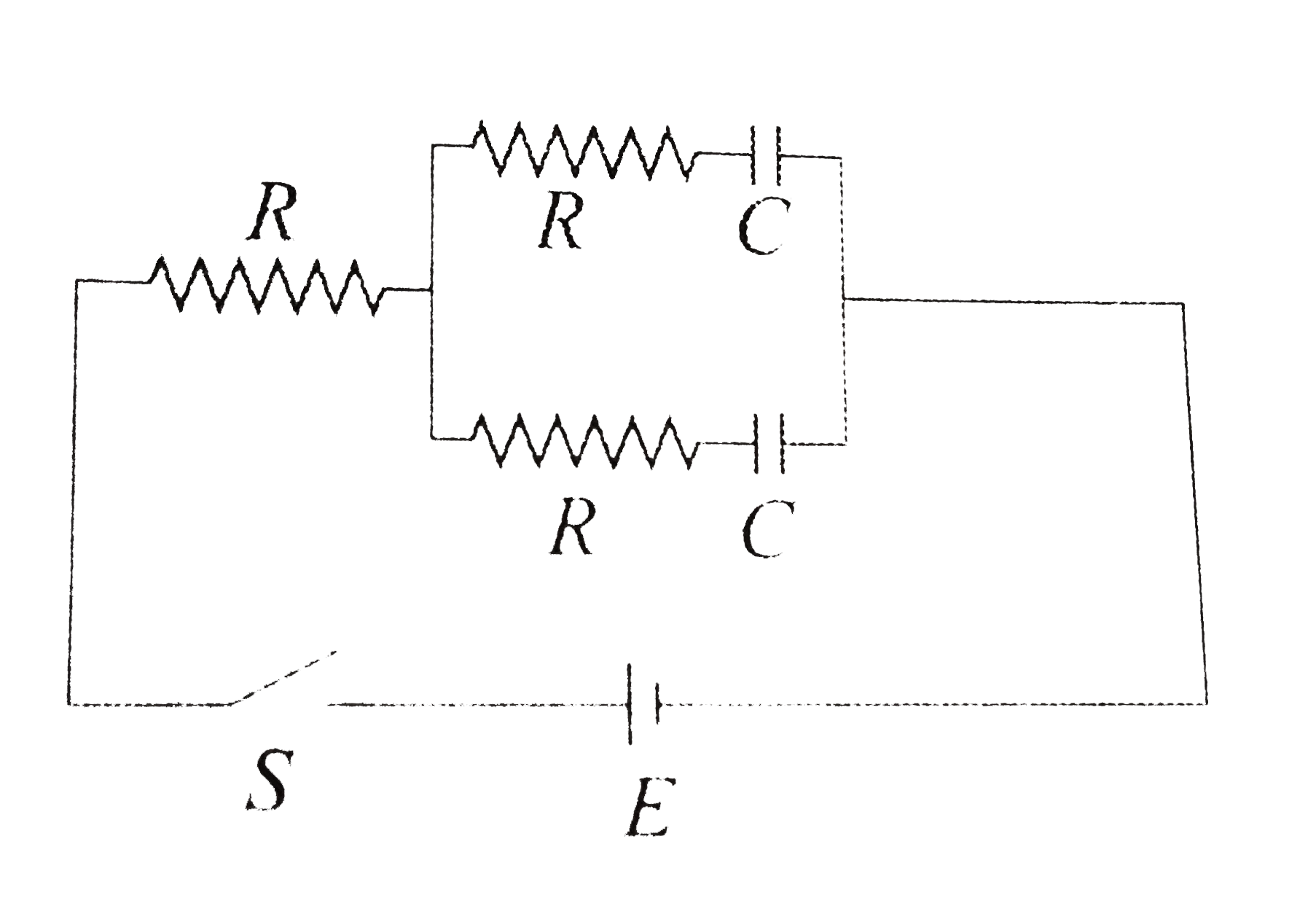
The switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
 View Solution
View SolutionIn the circuit in Fig. switch S1 was closed for a long time . At time t=0 the switch is opened.
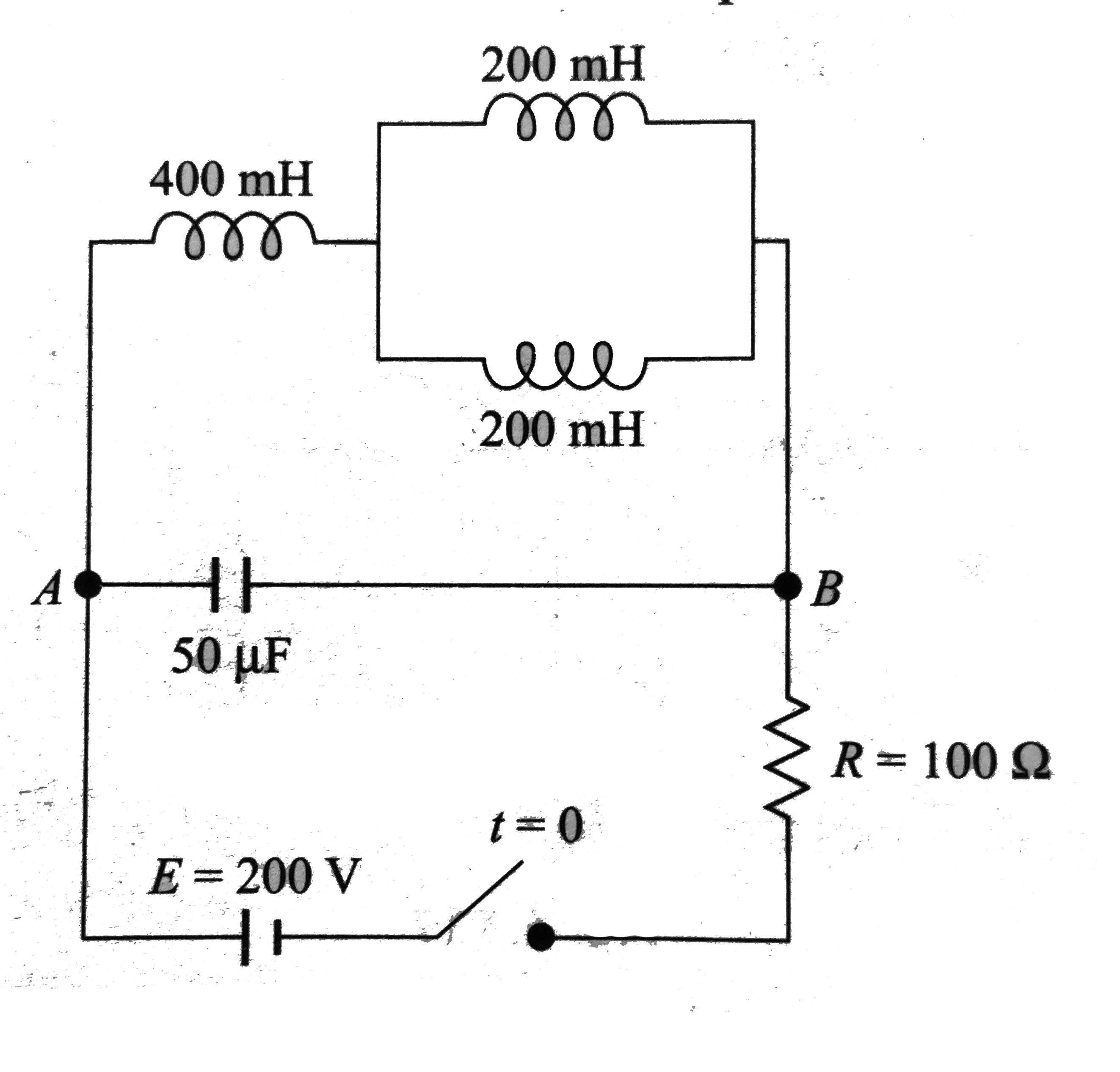
Find the angular frequency of oscillation of the charge on the capacitor.View SolutionTwo capacitors C1 and C2 are charged to same potential V, but with opposite polarity as shown in the figure. The switches S1 and S2 are then closed
 View Solution
View SolutionA capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
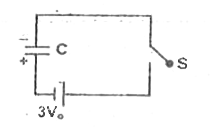
View Solutionn the circuit shown in the figure, the capacitor C is charged to a potential Vo The heat generated and charge flow, in the circuit to when the switch S is closed, is
 View Solution
View SolutionIn the circuit shown, the capacitor initially charged with a 12V batteryy, when switch S1 is open and switch S2 is closed. The maximum value of current in the circuit when S2 is opened and S2 is closed is
 View Solution
View SolutionTwo capacitors C1=4μFandC2=2μF are charged to same potential V = 500 Volt, but with opposite polarity as shown in the figure. The switches S1andS2 are closed.
 View Solution
View SolutionIn the circuit shown in the figure, if switches S1 and S2 have been closed for a long time, then charge on the capacitor.
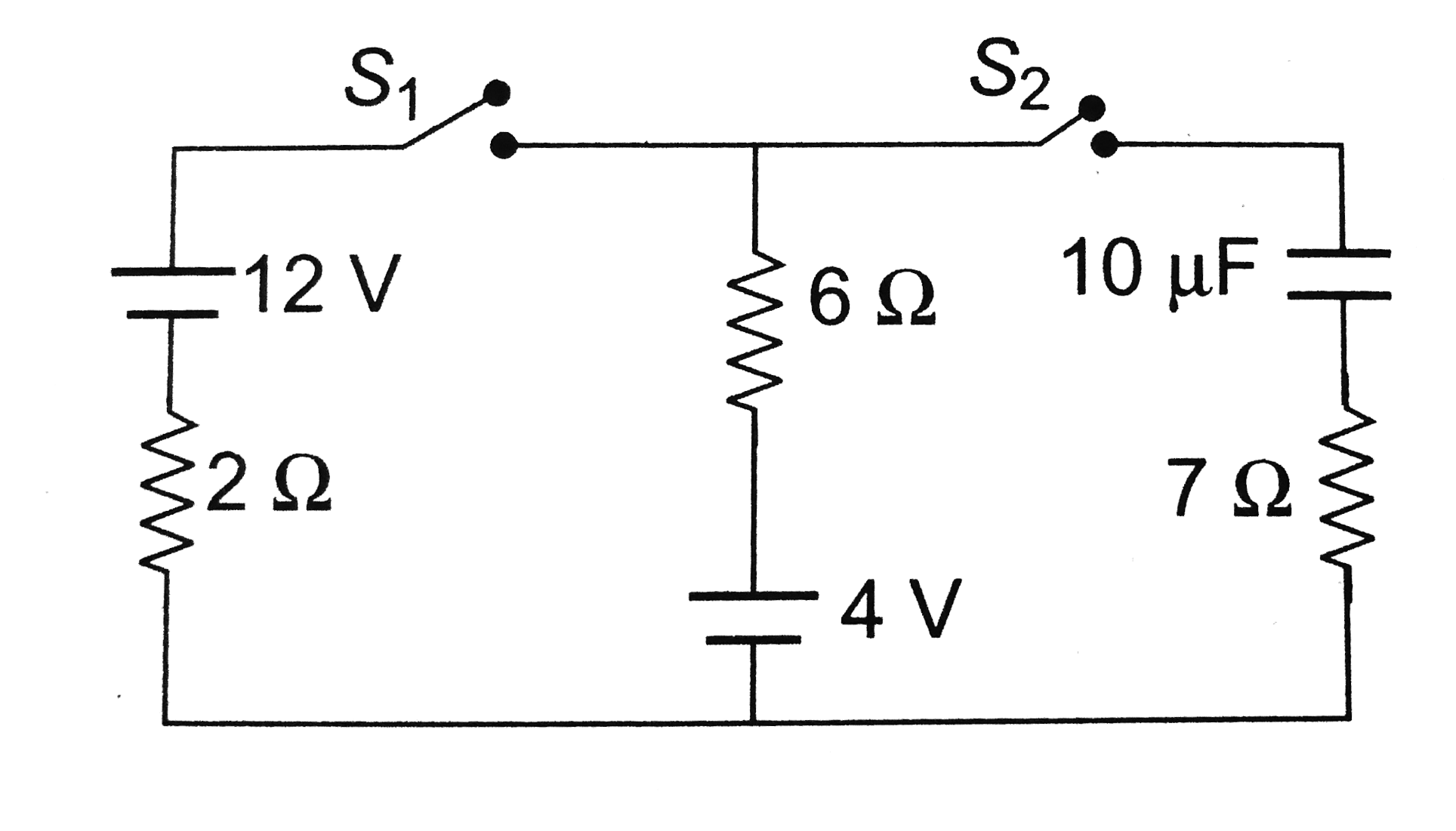 View Solution
View SolutionFor a circuit shown in figure 5.235 switch S1 is closed at t= 0, then at t=(2R2+R1)C,S1 is opened and S2 is closed.

a. Find the charge on capactior at t=(2R2+2R1)C.
b. Find current through R2 (adjacent to the battery) at t=(3R1+2R2)C.View SolutionIn the circuit shown in figure C1=2C2. Capacitance C1 is charged to a potential of V. The current in the circuit just after the switch S is closed is
 View Solution
View Solution
