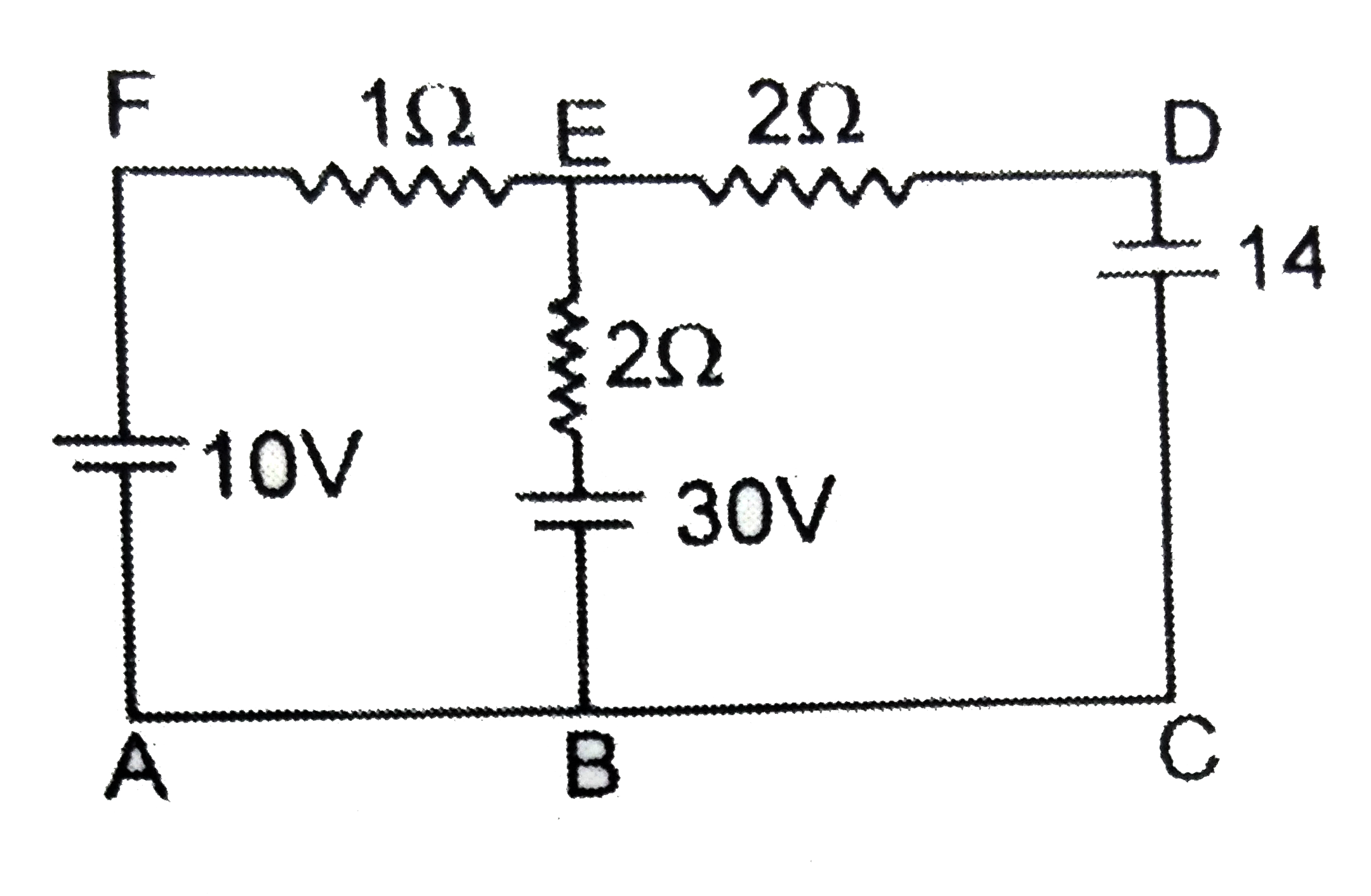
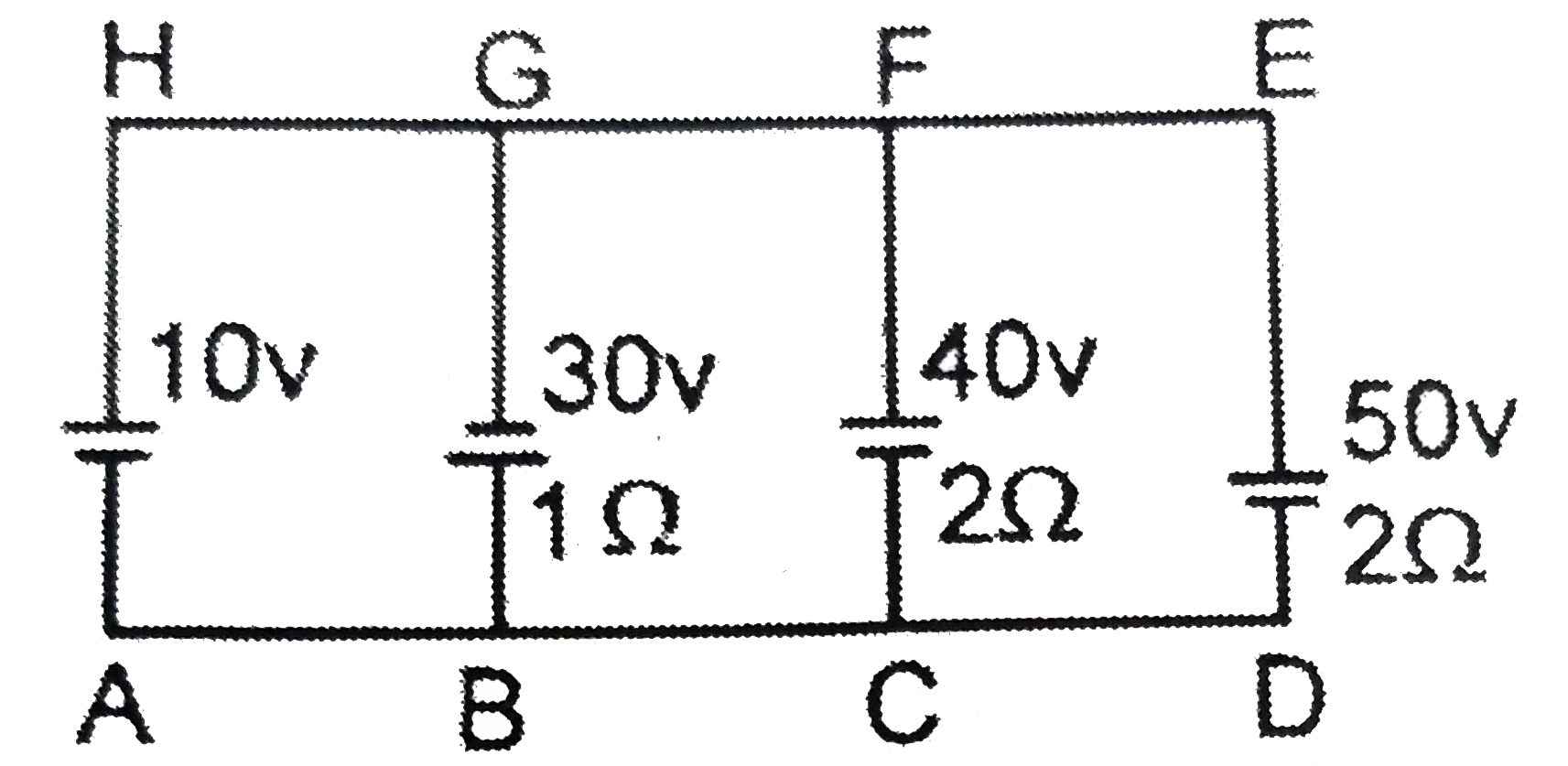
Find the current in each part of the circuit.
To find the current in each part of the circuit, we will apply Kirchhoff's laws. Let's break down the solution step by step.
Step 1: Identify the Circuit Components
We have a circuit with two resistors and two currents, I1 and I2. The voltage source is 4.5 V and we have resistances of 3 ohms and 6 ohms.
Step 2: Apply Kirchhoff's Voltage Law (KVL) to the First Loop
Starting from the voltage source (4.5 V) and moving through the resistors, we can write the equation for the first loop:
4.5−3I1−6(I1+I2)=0
This simplifies to:
4.5−3I1−6I1−6I2=0
Combining like terms:
4.5−9I1−6I2=0
Rearranging gives us:
9I1+6I2=4.5
Dividing the entire equation by 3:
3I1+2I2=1.5(Equation 1)
Step 3: Apply KVL to the Second Loop
Next, we apply KVL to the second loop, which includes a 3 V source:
3−10I2−6I1−6I2=0
This simplifies to:
3−6I1−16I2=0
Rearranging gives us:
6I1+16I2=3(Equation 2)
Step 4: Solve the System of Equations
Now we have two equations:
1. 3I1+2I2=1.5
2. 6I1+16I2=3
To eliminate I1, we can multiply Equation 1 by 2:
6I1+4I2=3(Equation 3)
Now we can subtract Equation 2 from Equation 3:
(6I1+4I2)−(6I1+16I2)=3−3
This simplifies to:
−12I2=0
Thus, we find:
I2=0
Step 5: Substitute I2 back to find I1
Now that we have I2=0, we can substitute this value back into Equation 1:
3I1+2(0)=1.5
This simplifies to:
3I1=1.5
Dividing both sides by 3 gives:
I1=0.5A
Final Results
- I1=0.5A
- I2=0A
We have a circuit with two resistors and two currents, I1 and I2. The voltage source is 4.5 V and we have resistances of 3 ohms and 6 ohms.
Starting from the voltage source (4.5 V) and moving through the resistors, we can write the equation for the first loop:
4.5−3I1−6(I1+I2)=0
This simplifies to:
4.5−3I1−6I1−6I2=0
Combining like terms:
4.5−9I1−6I2=0
Rearranging gives us:
9I1+6I2=4.5
Dividing the entire equation by 3:
3I1+2I2=1.5(Equation 1)
Next, we apply KVL to the second loop, which includes a 3 V source:
3−10I2−6I1−6I2=0
This simplifies to:
3−6I1−16I2=0
Rearranging gives us:
6I1+16I2=3(Equation 2)
Now we have two equations:
1. 3I1+2I2=1.5
2. 6I1+16I2=3
6I1+4I2=3(Equation 3)
(6I1+4I2)−(6I1+16I2)=3−3
This simplifies to:
−12I2=0
Thus, we find:
I2=0
Now that we have I2=0, we can substitute this value back into Equation 1:
3I1+2(0)=1.5
This simplifies to:
3I1=1.5
Dividing both sides by 3 gives:
I1=0.5A
- I1=0.5A
- I2=0A
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Solved Examples
Explore 12 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Exercise 5.1
Explore 28 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
Similar Questions
Knowledge Check
The figure below shows current in a part of electric circuit. The current i is
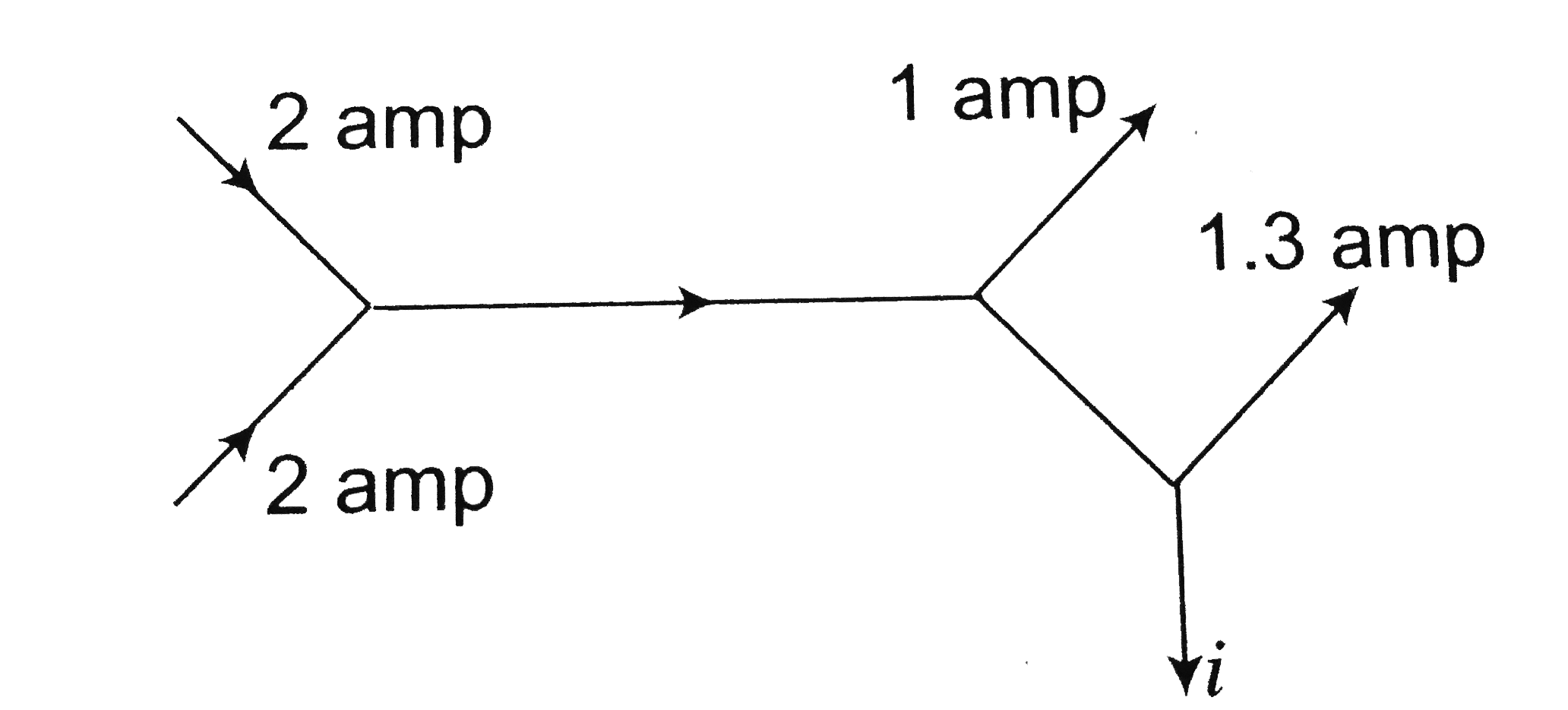 A1.7AB3.7AC1.3AD1A
A1.7AB3.7AC1.3AD1A
Find the current in each wire.

View SolutionFind the current in each resistor of the circuit shown in fig
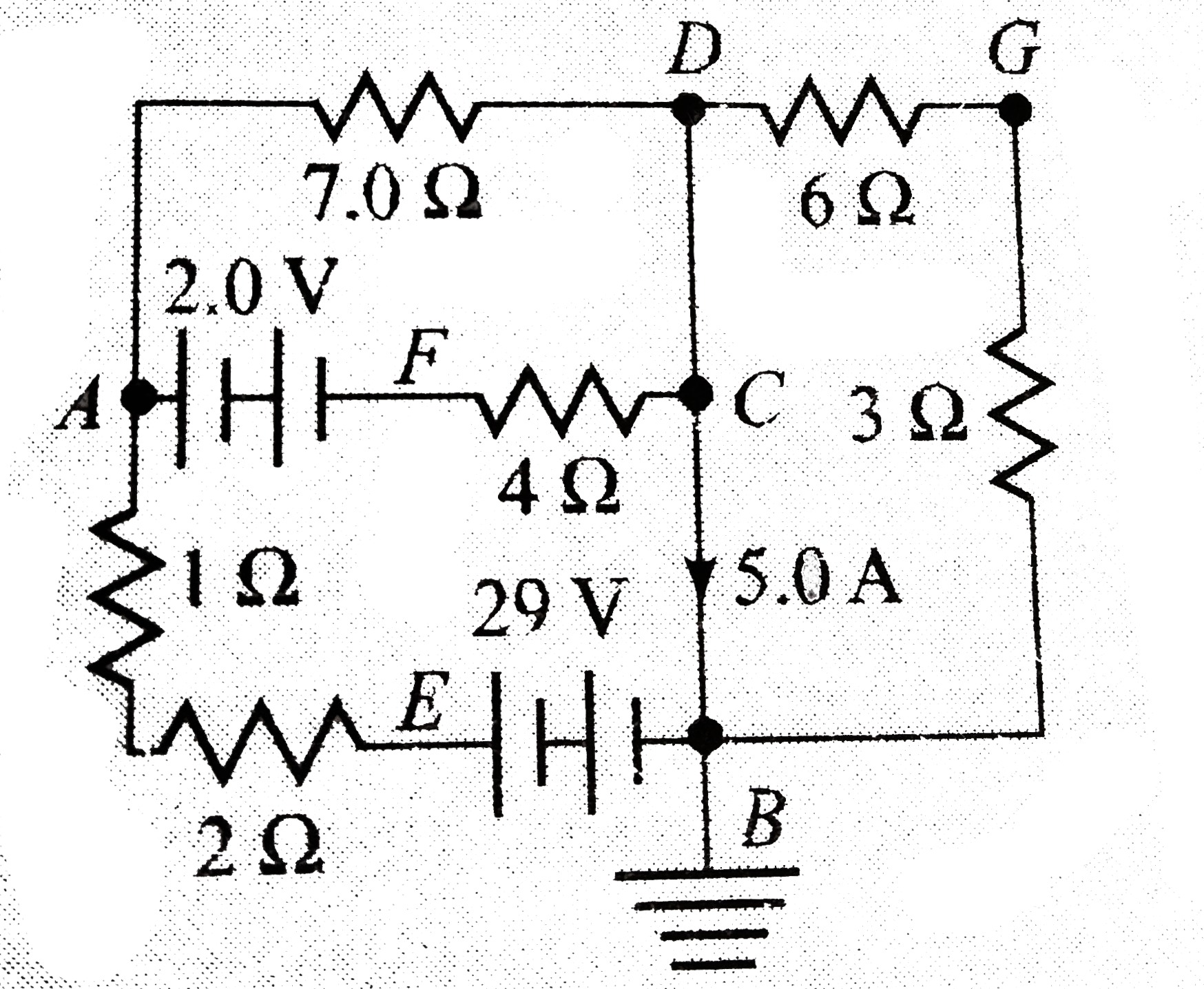
a. Current thorugh resistance of 6Ωis………..
b. Current thorugh resistance of 3Ωis………..
c. Current thorugh resistance of 2Ωis………..
d. Current thorugh resistance of 5Ωis………..
View SolutionFind the current in each branches of the circuit.
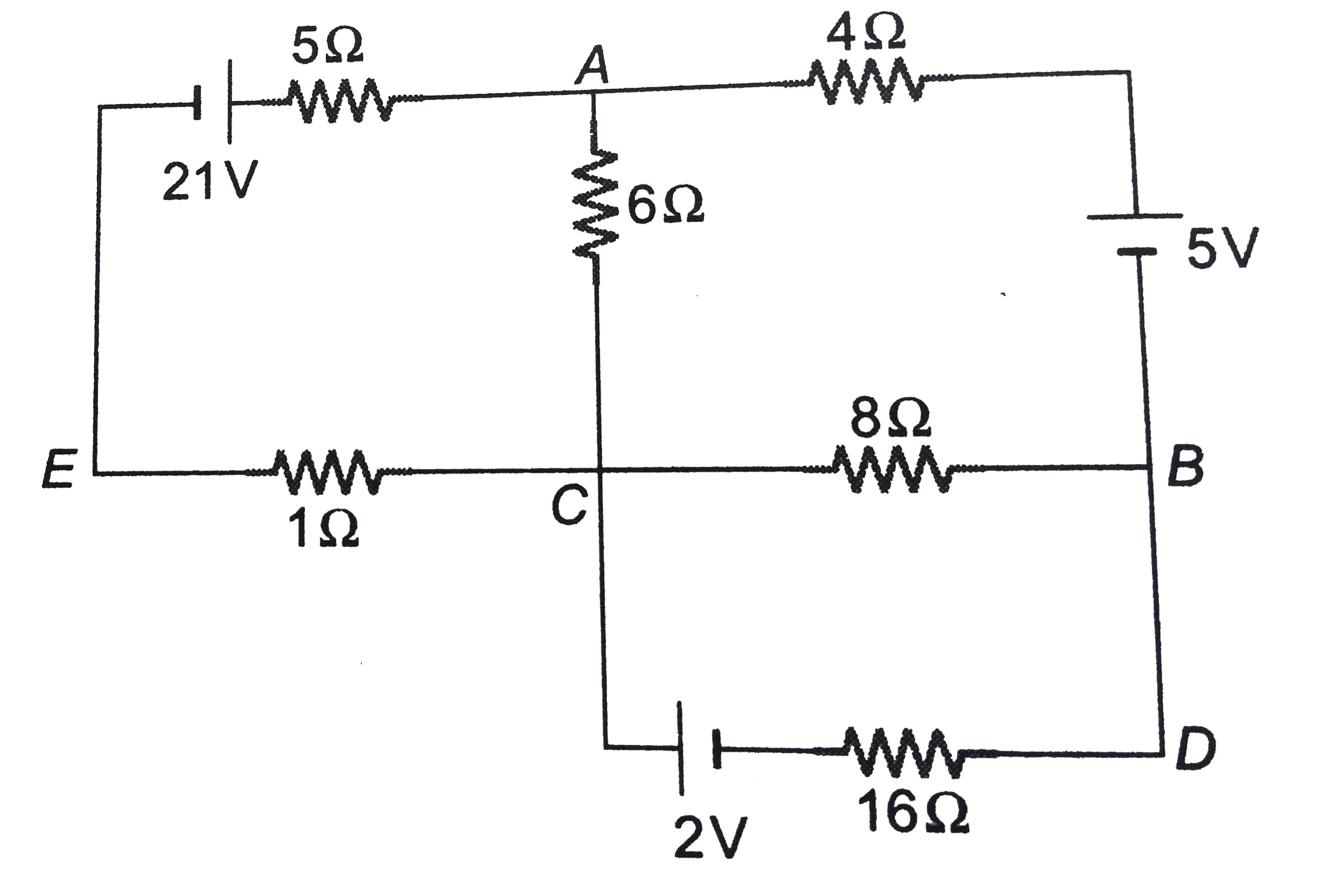
View SolutionFind the current in each resistor in the circuit as shown in fig.

View SolutionFind the current in the branch CD of the circuit (in ampere).
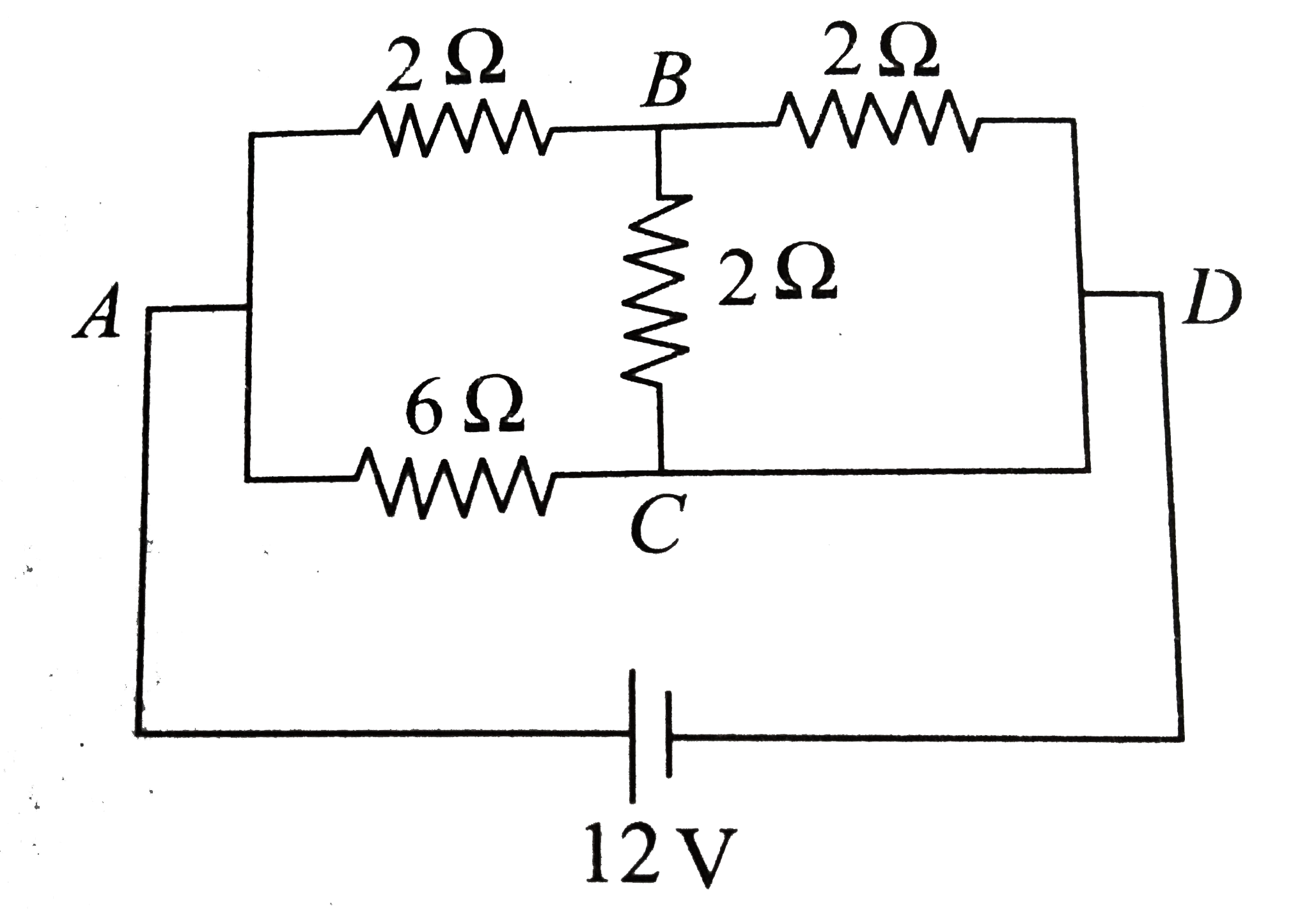
View SolutionFind the current in each branch f the given circuit in steady state. Find the charge on each capacitor.
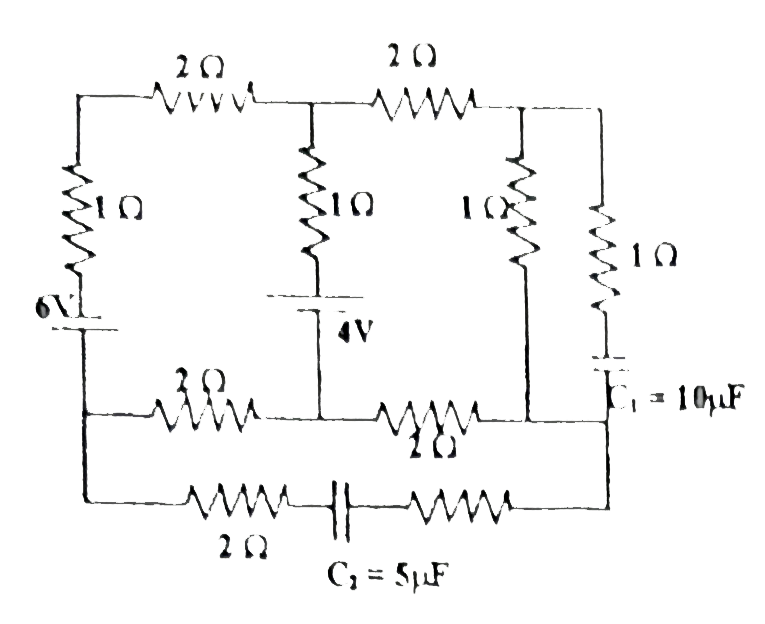
View SolutionFind the current in the circuit
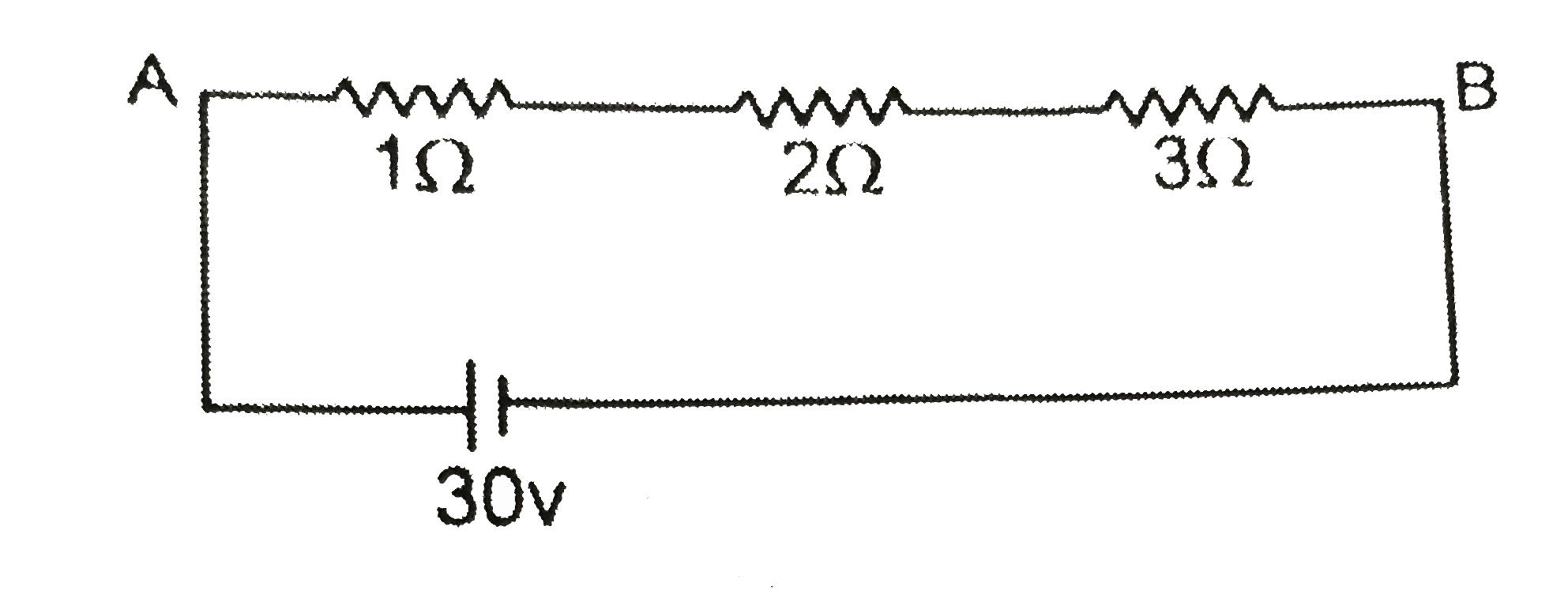
View Solution