A resistance R of therimal coefficient of resistivity α is connected in parallel with a resistance 3R. Having thermal coeffiecinet of resistivity 2α Find the value of αeff
To solve the problem step by step, we need to find the effective thermal coefficient of resistivity (α_eff) for two resistors connected in parallel.
Step 1: Identify the resistances and their thermal coefficients
- Let R1 = R with thermal coefficient of resistivity α.
- Let R2 = 3R with thermal coefficient of resistivity 2α.
Step 2: Calculate the equivalent resistance (R_eq) of the parallel combination
Using the formula for resistors in parallel:
1Req=1R1+1R2
Substituting the values:
1Req=1R+13R
Finding a common denominator:
1Req=3+13R=43R
Thus, the equivalent resistance is:
Req=3R4
Step 3: Relate the resistances to their thermal coefficients
The resistance at a temperature T can be expressed as:
- For R1:
R1(T)=R(1+αT)
- For R2:
R2(T)=3R(1+2αT)
Step 4: Substitute the resistances into the equivalent resistance formula
The equivalent resistance at temperature T can also be expressed as:
Req(T)=Req(0)(1+αeffT)
Where Req(0) is the equivalent resistance at 0°C.
Step 5: Calculate Req(0)
At 0°C, using the equivalent resistance we found:
Req(0)=3R4
Step 6: Substitute the expressions for R1 and R2 into the equivalent resistance formula
Now, we can write:
3R4=R(1+αT)⋅3R(1+2αT)R(1+αT)+3R(1+2αT)
Step 7: Simplify the equation
This leads to:
3R(1+2αT)(1+αT)R(1+αT)+3R(1+2αT)=3(1+2αT)(1+αT)(1+αT)+3(1+2αT)
Step 8: Solve for αeff
After simplifying and equating the coefficients, we find that:
αeff=54α
Final Answer
Thus, the effective thermal coefficient of resistivity is:
αeff=54α
---
- Let R1 = R with thermal coefficient of resistivity α.
- Let R2 = 3R with thermal coefficient of resistivity 2α.
Using the formula for resistors in parallel:
1Req=1R1+1R2
Substituting the values:
1Req=1R+13R
Finding a common denominator:
1Req=3+13R=43R
Thus, the equivalent resistance is:
Req=3R4
The resistance at a temperature T can be expressed as:
- For R1:
R1(T)=R(1+αT)
- For R2:
R2(T)=3R(1+2αT)
The equivalent resistance at temperature T can also be expressed as:
Req(T)=Req(0)(1+αeffT)
Where Req(0) is the equivalent resistance at 0°C.
At 0°C, using the equivalent resistance we found:
Req(0)=3R4
Now, we can write:
3R4=R(1+αT)⋅3R(1+2αT)R(1+αT)+3R(1+2αT)
This leads to:
3R(1+2αT)(1+αT)R(1+αT)+3R(1+2αT)=3(1+2αT)(1+αT)(1+αT)+3(1+2αT)
After simplifying and equating the coefficients, we find that:
αeff=54α
Thus, the effective thermal coefficient of resistivity is:
αeff=54α
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples
12 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.1
28 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
Value of the resistance R in the figure is
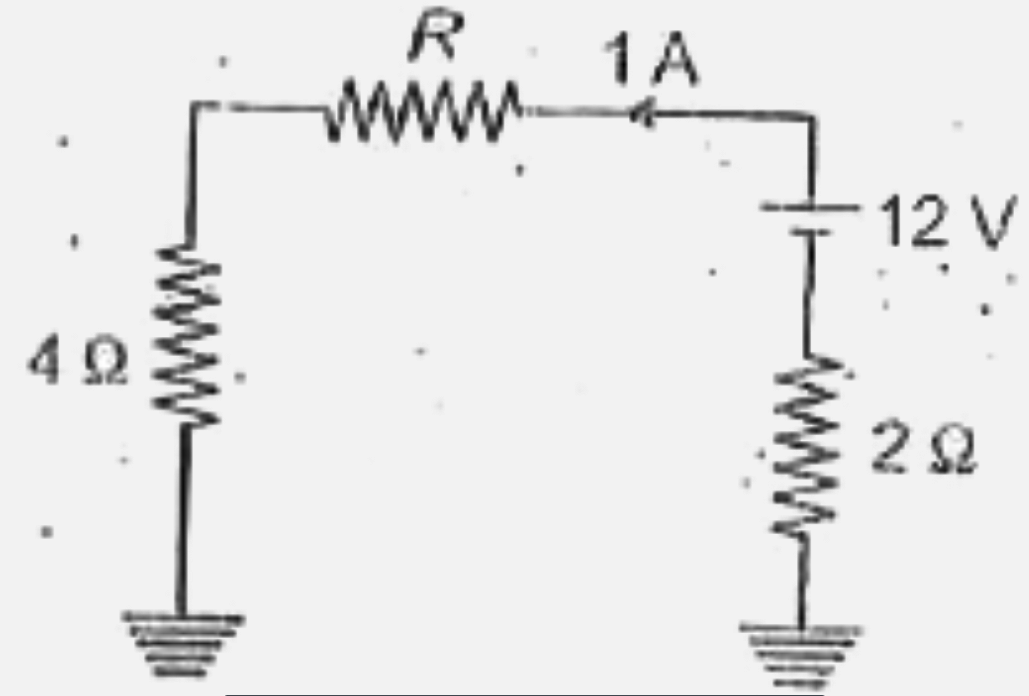
View SolutionValue of the resistance R in the figure is
View SolutionFind out the value of resistance R in fig.
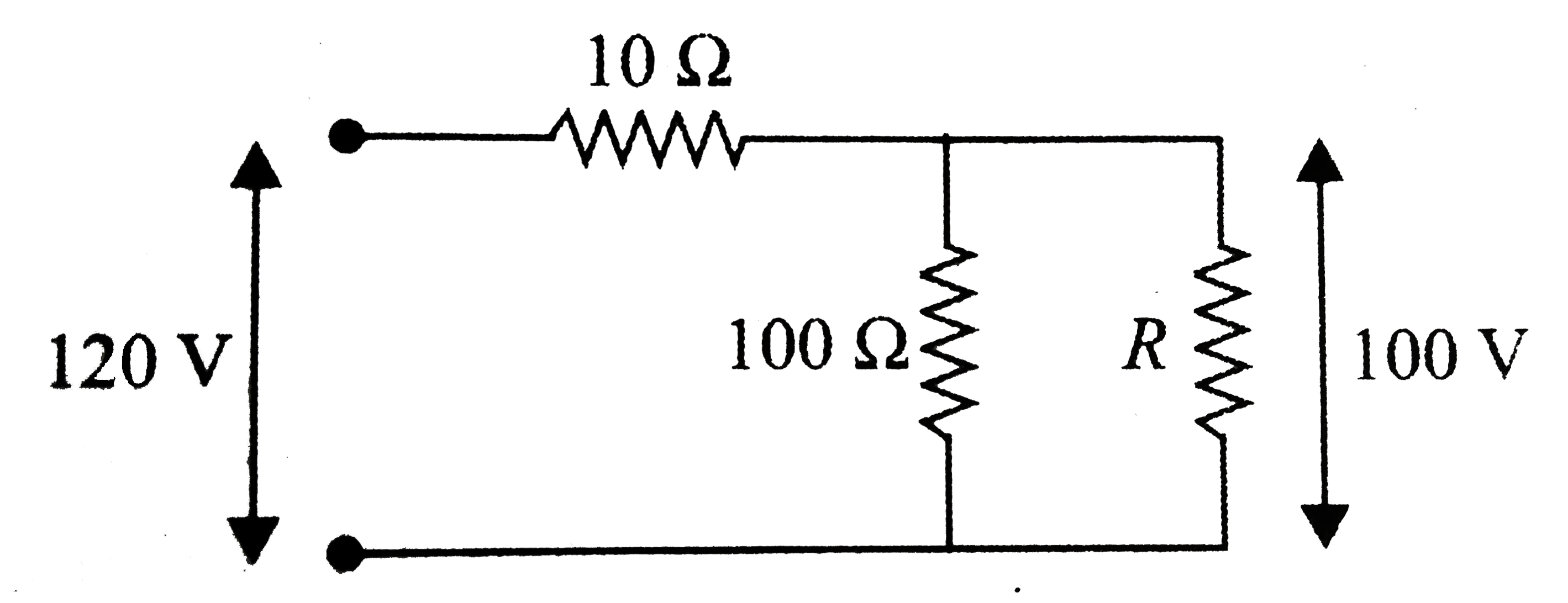
View SolutionTwo resistors having resistance 4 Ω and 6 Ω are connected in parallel. Find their equivalent resistance.
View SolutionA wire of resistance R is divided in 10 equal parts. These parts are connected in parallel, the equivalent resistance of such connection will be
View SolutionAn ammeter has resistance R0 and range l what resistance should be connected in parallel with it to increase its range by nl ?
View SolutionTwo equal resistance at 0∘C with temperature coefficient of resistance α1 and α2 joined in series act as a single resistance in a circuit the temperature coefficient of their single resistance will be
View SolutionThe resistance of a series combination of the resistance is S. when they are joined in parallel equvalent resistance is P. Find the value of (S2P)
View SolutionIn the circuit shown in figure, if a resistance R connected in parallel with R2, then match following
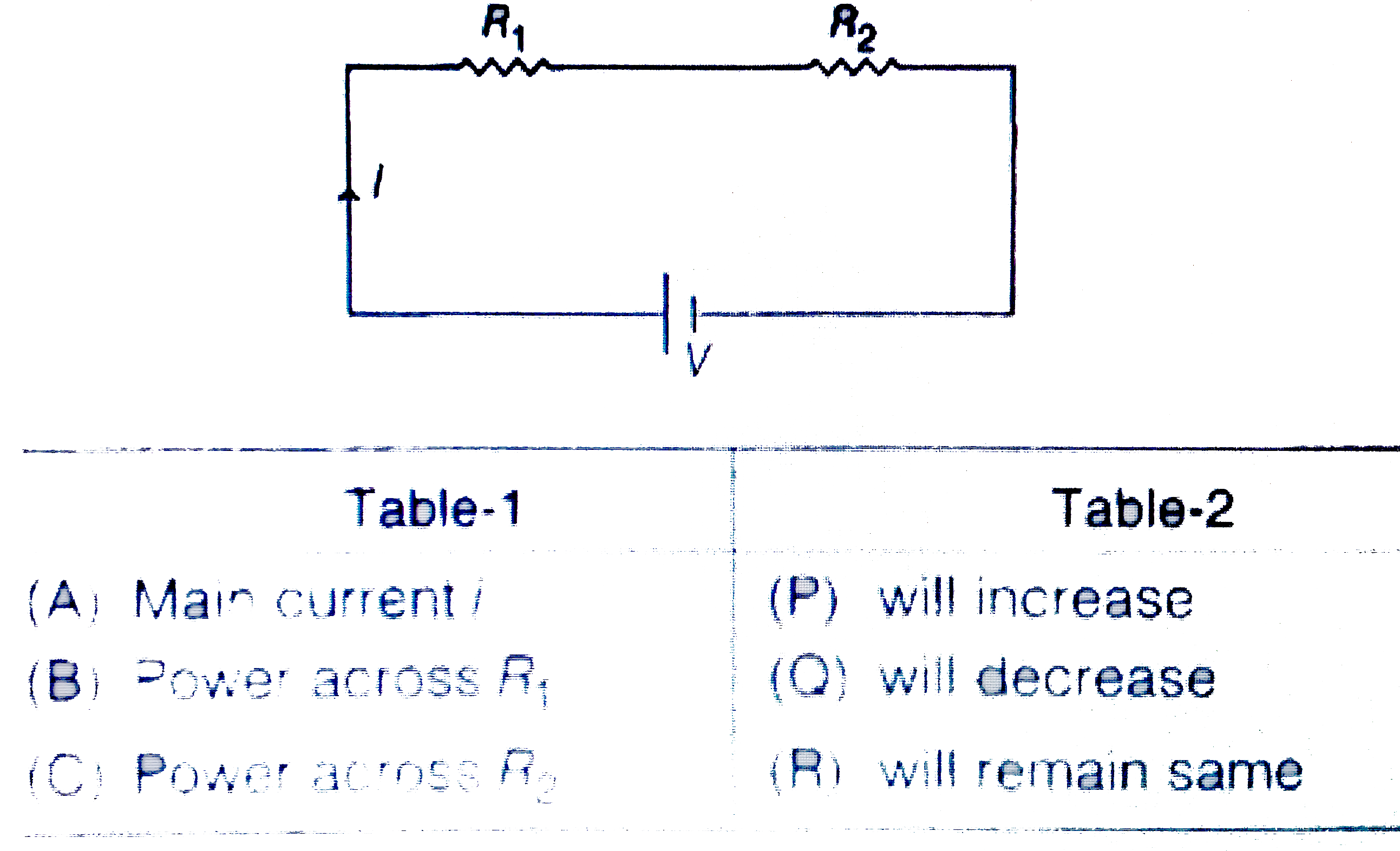
View SolutionTwo metallic wires. A and B of equal dimensions but made of different materials, having resistivities p and 2p temperature coefficients of resistivities 2aipha and α, are connected in series. The temperature coefficient of resistance of the composite wire equals
View Solution

