Find the approximate total distance traveled by an electron in the time interval in which its displacement in one meter along the wire.
To solve the problem of finding the approximate total distance traveled by an electron in the time interval during which its displacement is 1 meter along a wire, we can follow these steps:
1. Identify the Given Data:
- Displacement (s) = 1 meter
- Drift velocity (Vd) = 1 mm/s = 1×10−3 m/s
2. Calculate the Time Interval (t):
- The time taken to travel the length of the wire can be calculated using the formula:
t=sVd
- Substituting the values:
t=1 m1×10−3 m/s=1000 seconds=103 seconds
3. Determine the Speed of the Electron:
- The average speed of an electron between two successive collisions is approximately 106 m/s.
4. Calculate the Total Distance Traveled by the Electron:
- The total distance traveled can be calculated using the formula:
Distance=Speed×Time
- Substituting the values:
Distance=(106 m/s)×(103 s)=109 meters
5. Final Result:
- The approximate total distance traveled by the electron is 109 meters.
Summary:
The total distance traveled by the electron in the time interval during which it displaces 1 meter along the wire is approximately 109 meters.
---
- Displacement (s) = 1 meter
- Drift velocity (Vd) = 1 mm/s = 1×10−3 m/s
- The time taken to travel the length of the wire can be calculated using the formula:
t=sVd
- Substituting the values:
t=1 m1×10−3 m/s=1000 seconds=103 seconds
- The average speed of an electron between two successive collisions is approximately 106 m/s.
- The total distance traveled can be calculated using the formula:
Distance=Speed×Time
- Substituting the values:
Distance=(106 m/s)×(103 s)=109 meters
- The approximate total distance traveled by the electron is 109 meters.
The total distance traveled by the electron in the time interval during which it displaces 1 meter along the wire is approximately 109 meters.
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples
12 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.1
28 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
Knowledge Check
Which of the following statements is incorrect? a) Displacement is independent of the choice of origin of the axis. b) Displacement may or may not be equal to the distance travelled. c) When a particle returns to its starting point, its displacement is not zero. d) Displacement does not tell the nature of the actual motion of a particle between the points.
ADisplacement is independent of the choice of origin of the axis.BDisplacement may or may not be equal to the distance travelled.CWhen a particle returns to its starting point, its displacement is not zero.DDisplacement does not tell the nature of the actual motion of a particle between the points.
State how the velocity-time graph can be used to find (i) the acceleration of a body, (ii) the distance travelled by the body in a given time, and (iii) the displacement of the body in a given time.
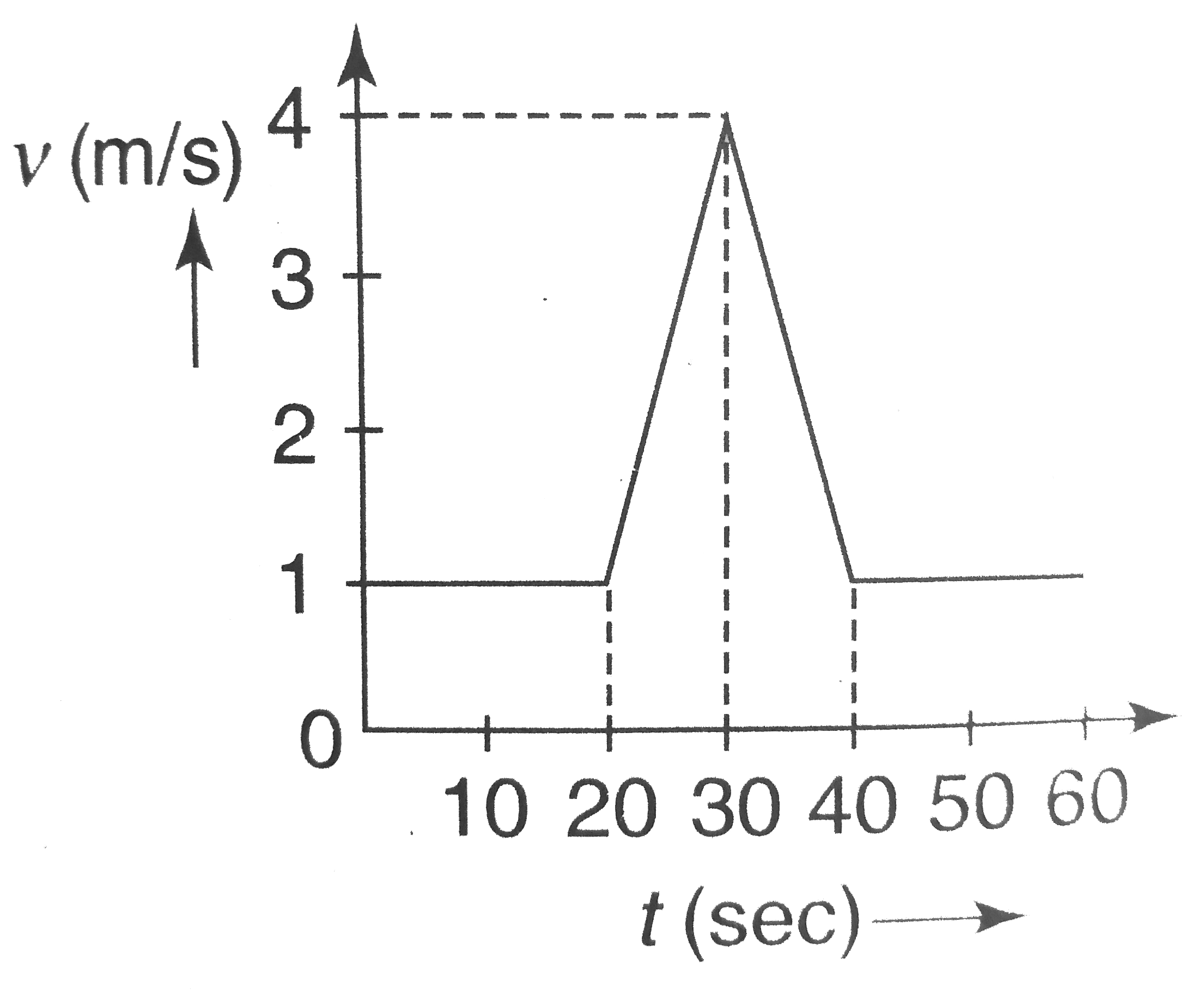
View SolutionVelocity-time (v-t) graph for a moving object is shown in the figure. Total displacement of the object during the time interval when there is non-zero acceleration and retardation is

View SolutionVelocity -time (v-t) graph for a moving object is shown in the figure .Total displacement of the object during the time interval when there is non-zero acceleration and reatardation is

View SolutionVelocity-time graph for a moving object is shown in the figure. Total displacement of the object during the time interval when there is non-zero acceleration and retardation is.
View SolutionWhat is the ratio between the distance travelled by the oscillator in one time period and amplitude?
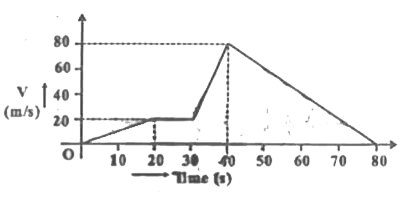
View SolutionThe velocity-time graph of a moving object is given in the figure. Draw the acceleration versus time and displacement versus time graph. Find the distance travelled during the time interval when the acceleration is maximum . Assume that the particle starts from origin.
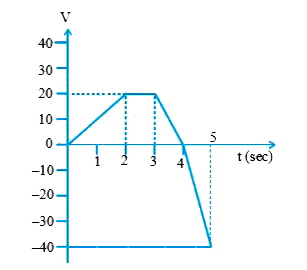
View SolutionIn the following velocity time graph of a body the distance travelled by the body and its displacement during 5 second in meter will be:
View Solution
