At which of the two points, 1 or 2, of a charged capacitor with nonparallel plates is the surface charge density greater?
To determine at which of the two points, 1 or 2, of a charged capacitor with non-parallel plates the surface charge density is greater, we can follow these steps:
Step 1: Understand the Configuration
We have a capacitor with non-parallel plates. The surface charge density (σ) is related to the electric field (E) produced by the charged plates.
Step 2: Recall the Relationship Between Electric Field and Surface Charge Density
The electric field (E) between two plates of a capacitor is given by the formula:
\( E = \frac{\sigma}{\epsilon_0} \)
where:
- \( \sigma \) is the surface charge density,
- \( \epsilon_0 \) is the permittivity of free space.
Step 3: Analyze the Electric Field in Non-Parallel Plates
For non-parallel plates, the distance (D) between the plates varies. The electric field is inversely proportional to the distance between the plates. Therefore, if the distance is greater, the electric field will be smaller.
Step 4: Compare the Distances at Points 1 and 2
Assume that point 1 is closer to one plate and point 2 is further away. Since point 2 is at a greater distance from the charged plate, the electric field at point 2 will be smaller than at point 1.
Step 5: Relate Electric Field to Surface Charge Density
Since we established that:
\( E \propto \sigma \)
If \( E_2 < E_1 \), then it follows that:
\( \sigma_2 < \sigma_1 \)
Step 6: Conclusion
Thus, the surface charge density at point 1 is greater than at point 2:
\( \sigma_1 > \sigma_2 \)
Final Answer
The surface charge density is greater at point 1 than at point 2.
---
We have a capacitor with non-parallel plates. The surface charge density (σ) is related to the electric field (E) produced by the charged plates.
The electric field (E) between two plates of a capacitor is given by the formula:
\( E = \frac{\sigma}{\epsilon_0} \)
where:
- \( \sigma \) is the surface charge density,
- \( \epsilon_0 \) is the permittivity of free space.
For non-parallel plates, the distance (D) between the plates varies. The electric field is inversely proportional to the distance between the plates. Therefore, if the distance is greater, the electric field will be smaller.
Assume that point 1 is closer to one plate and point 2 is further away. Since point 2 is at a greater distance from the charged plate, the electric field at point 2 will be smaller than at point 1.
Since we established that:
\( E \propto \sigma \)
If \( E_2 < E_1 \), then it follows that:
\( \sigma_2 < \sigma_1 \)
Thus, the surface charge density at point 1 is greater than at point 2:
\( \sigma_1 > \sigma_2 \)
The surface charge density is greater at point 1 than at point 2.
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Exercise 4.2
Explore 32 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Subjective
Explore 24 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Solved Examples
Explore 10 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:ATOMIC PHYSICSExercise:ddp.4.3
Explore 15 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
Similar Questions
The plates of a parallel plate capacitor are not exactly parallel. The surface charge density is therefore,
View SolutionIf the two plates of the charged capacitor are connected by a wire, then
View SolutionIf a small sphere of mass m and charge q is hanged from a silk thread at an angle θ with the surface of a vertical charged conducting plate, then for equilibrium of sphere the surface charge density of the plate -
View SolutionIf a small sphere of mass m and charge q is hung from a silk thread at an angle θ with the surface of a vertical charged conducting plate, then for equilibrium of sphere, the surface charge density of the plate is
View SolutionConsider a parallel plate capacitor having charge Q. Then,
View SolutionA parallel plate capacitors of plate area A has a total surface charge density +σ on one plate and a total surface charge density −σ on the other plate. The force one plate due to the other plate is given by :
View SolutionTwo nonconducting plates A and B of radii 2R and 4R, respectively, are kept at distance x and 2x from the point charge q. A surface cutout of a nonconducting shell A is kept such that is center coincides with the point charge. Each plate and spherical surface carries surface charge density σ.
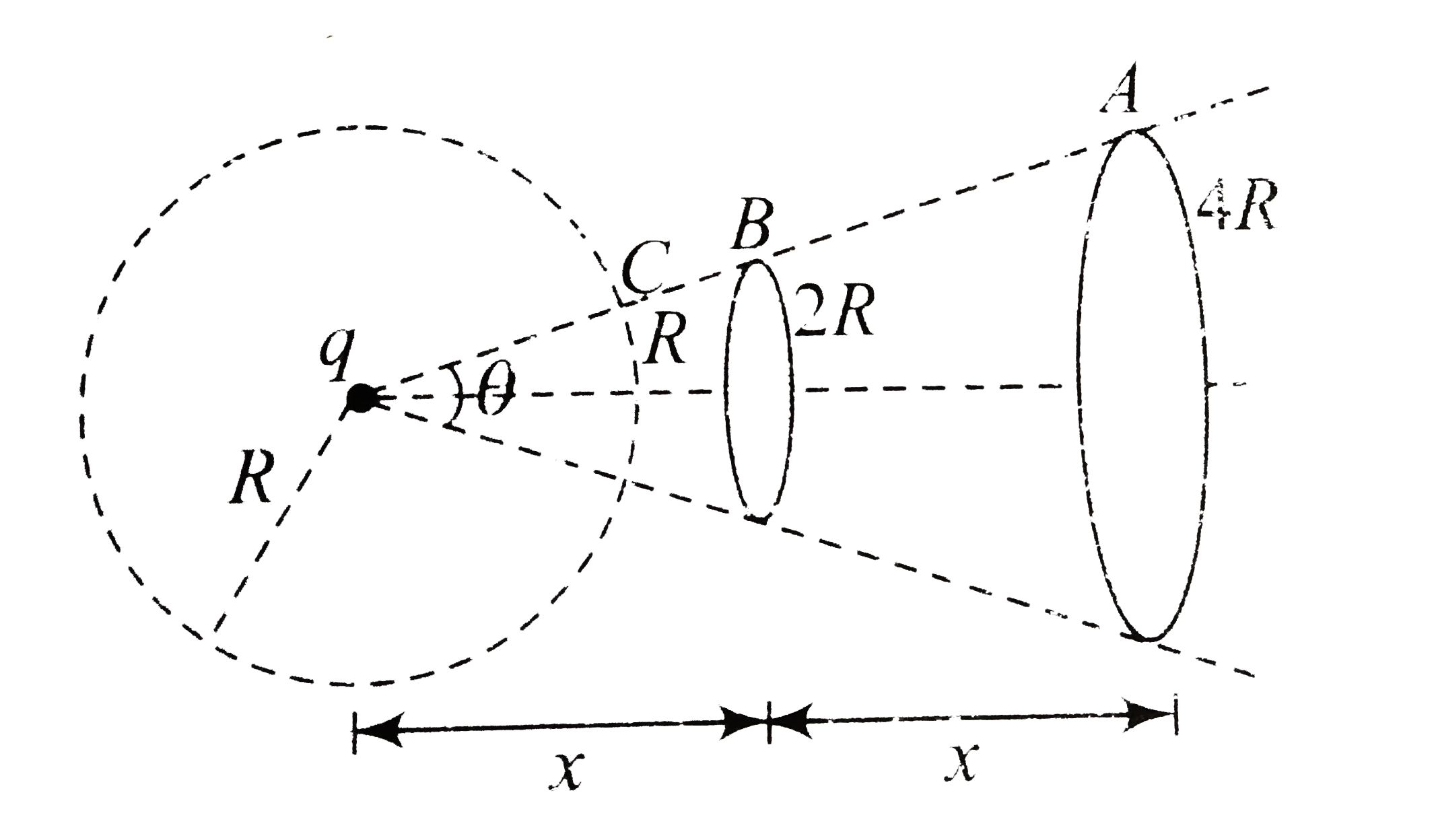
If FA,FB,andFC are the forces on plate A, plate B, and spherical surface C due to charge q, respectively, then
View SolutionAnswer the following:
(i) If two similar large plates, each of area A having surface charge densities +σ and −σ are separated by a distance d in air,find the expression for
(a) field at points between the two plates and on outer side of the plates. Specify the direction of the field in each case.
(b) the potential difference between the plates.
(c) the capacitance of the capacitor so formed.
(ii) Two metallic spheres of radii R and 2R are charged so that both of these have same surface charge density σ. If they are connected to each other with a conducting wire, in which direction will the charge flow and why ?
View SolutionAn electron moves staright inside a charged parallel plate capacitor of unifrom surface charge dencity σ. The space between the plates is filled with constant magnetic field of induction →B. The time of staright line motion of the electron in the capacitor is

View SolutionAn electron moves staright inside a charged parallel plate capacitor of unifrom surface charge dencity σ. The space between the plates is filled with constant magnetic field of induction →B. The time of staright line motion of the electron in the capacitor is

View Solution