Positive charge Q is uniformly distributed throughout the volume of a sphere of radius R. A Point mass having charge +q and mass m is fired towards the centre of the sphere with velocity v from a point A at distance r(r>R) from the centre of the sphere. Find the minimum, so that it can penetrate R/2 distance of the sphere. Neglect any resistance other than:e-c141::, interaction. Charge on the small mass remains constant throughout the motion
Using conservation of mechanical energy ΔK+ΔU=0,
(0−12mv2)+q(Vf−Vi)=0
or 12mv2=q(Vf−Vi) ….(i)
Vi=Q4πε0randVf=q8πε0R[3−r2R2]
where r=R2,here,Vf=11Q32πε0R
Putting the values of Vi and Vf in Eq. (i)
12mv2=11qQ32πε0R−qQ4πε0r
or mv2=11qQ16πε0R−qQ2πε0r
=qQ2πε0[118R−1r]
or v2=qQ2mπε0R[118−Rr]
Hence V=√qQ2mπε0R[118−Rr].
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Examples9videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.123videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q2videos
ELECTRICAL MEASURING INSTRUMENTS
Similar Questions
A positive charge Q is uniformly distributed throughout the volume of a dielectric sphere of radius R. A point mass having charge +q and mass m is fired toward the center of the sphere with velocity v from a point at distance r(r>R) from the center of the sphere. Find the minimum velocity v so that it can penetrate (R/2) distance of the sphere. Neglect any resistance other than electric interaction. Charge on the small mass remains constant throughout the motion.
 View Solution
View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :
 View Solution
View SolutionA charge +Q, is uniformaly distributed within a sphere of radius R. Find the electric field, due to this charge distribution, at a point distant r form the centre of the spehre where :
(i) 0<r<R and
(ii)r>RView SolutionA charge Q is uniformly distributed over the surface of two conducting concentric spheres of radii R and r (Rgtr). Then, potential at common centre of these spheres is
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.
 View Solution
View SolutionA charge is uniformly distributed inside a spherical body of radius r1=2r0 having a concetric cavity of radius r2=r0 (ρ is charge density inside the sphere). The potential of a point P at a distance 3r02 from the centre is
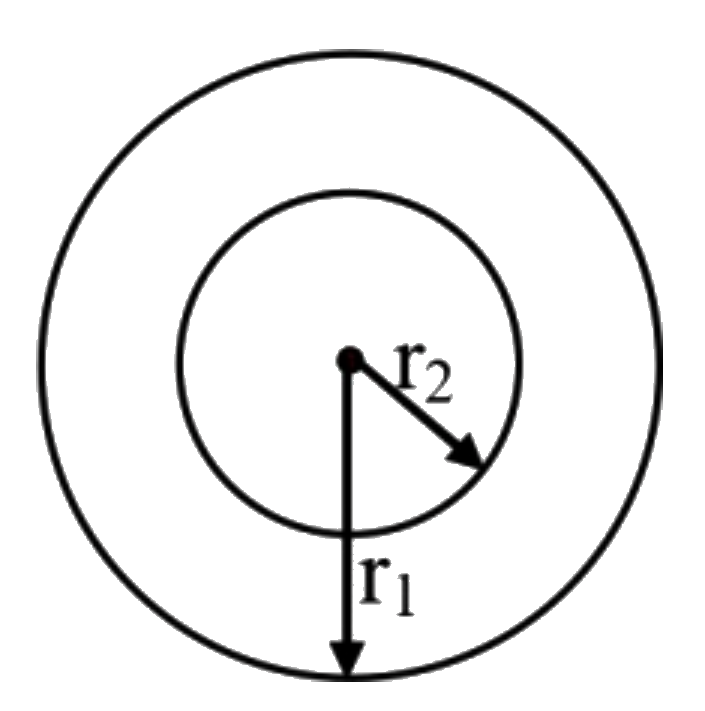 View Solution
View SolutionA bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)
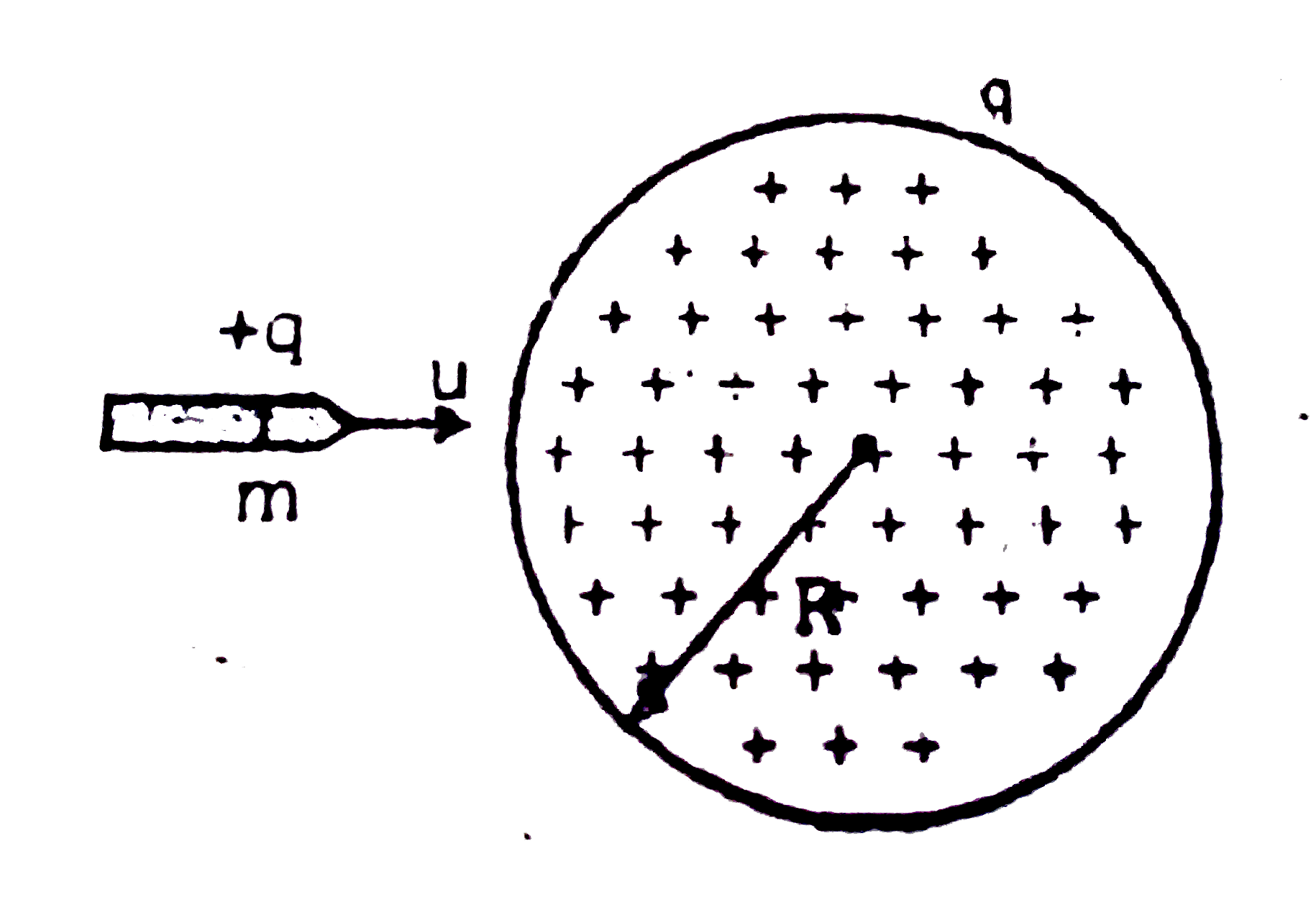 View Solution
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be
 View Solution
View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View Solution
