A metal sphere A of radius a is charged to potential V. What will be its potential if it is enclosed by a spherical conducting shell B of radius b and the two are connected by a wire ?
To solve the problem, we need to analyze the situation step by step:
Step 1: Understand the Initial Conditions
- We have a metal sphere A with a radius a that is charged to a potential V.
- The potential V of a charged sphere is given by the formula:
V=kQr
where k is Coulomb's constant, Q is the charge on the sphere, and r is the distance from the center of the sphere to the point where the potential is being measured.
Step 2: Connect the Sphere to the Conducting Shell
- When the metal sphere A is enclosed by a spherical conducting shell B of radius b and the two are connected by a wire, they will reach the same electric potential because conductors in electrostatic equilibrium have the same potential.
Step 3: Determine the Charge Distribution
- Initially, the charge Q is on sphere A. When connected by a wire, the charge will redistribute. The charge will move to the outer surface of the conducting shell B.
- The potential of the outer shell (which now has all the charge) can be expressed as:
V′=kQb
where b is the radius of the outer shell.
Step 4: Equate the Potentials
- Since both the sphere A and the shell B are at the same potential after being connected by the wire, we have:
V=V′=kQb
Step 5: Solve for the New Potential
- From the initial potential V of sphere A, we can express the charge Q as:
Q=V⋅ak
- Substituting Q into the equation for the potential of the outer shell gives:
V=k(V⋅ak)b
Simplifying this, we find:
V=V⋅ab
Final Result
- Thus, the potential of the metal sphere A when enclosed by the conducting shell B and connected by a wire is:
V′=V⋅ab
- We have a metal sphere A with a radius a that is charged to a potential V.
- The potential V of a charged sphere is given by the formula:
V=kQr
where k is Coulomb's constant, Q is the charge on the sphere, and r is the distance from the center of the sphere to the point where the potential is being measured.
- When the metal sphere A is enclosed by a spherical conducting shell B of radius b and the two are connected by a wire, they will reach the same electric potential because conductors in electrostatic equilibrium have the same potential.
- Initially, the charge Q is on sphere A. When connected by a wire, the charge will redistribute. The charge will move to the outer surface of the conducting shell B.
- The potential of the outer shell (which now has all the charge) can be expressed as:
V′=kQb
where b is the radius of the outer shell.
- Since both the sphere A and the shell B are at the same potential after being connected by the wire, we have:
V=V′=kQb
- From the initial potential V of sphere A, we can express the charge Q as:
Q=V⋅ak
- Substituting Q into the equation for the potential of the outer shell gives:
V=k(V⋅ak)b
Simplifying this, we find:
V=V⋅ab
- Thus, the potential of the metal sphere A when enclosed by the conducting shell B and connected by a wire is:
V′=V⋅ab
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Examples
9 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.1
23 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
A metal sphere A of radius a is charged to potential V. What will be its potential if it is enclosed by a spherical conducting shell B of radius b and the two are connected by a wire ?
View SolutionA hollow metallic sphere of radius 0.1 m is charged to a potential of 5 V. The potential at its centre is
View Solution
Knowledge Check
Metallic sphere of radius R is charged to potential V. Then charge q is proportional to
AVBRCboth V and RDnone of these
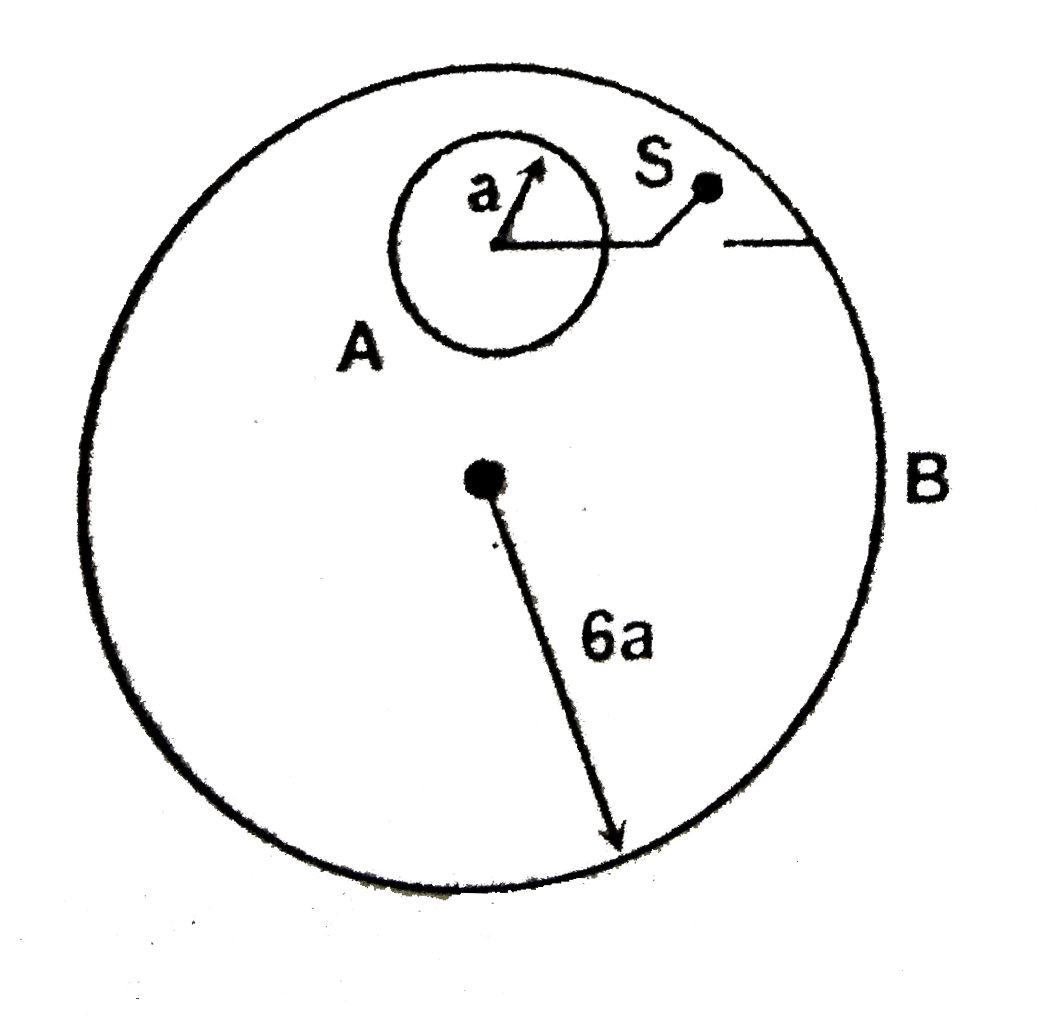
A small spherical conductor 'A' of radias 'a' is initially charged to a potential 'V' and then placed inside an uncharged spherical conducting shell 'B' of radius 6a as shown. The potential of the spherical conductor 'A' after closing the switch S is
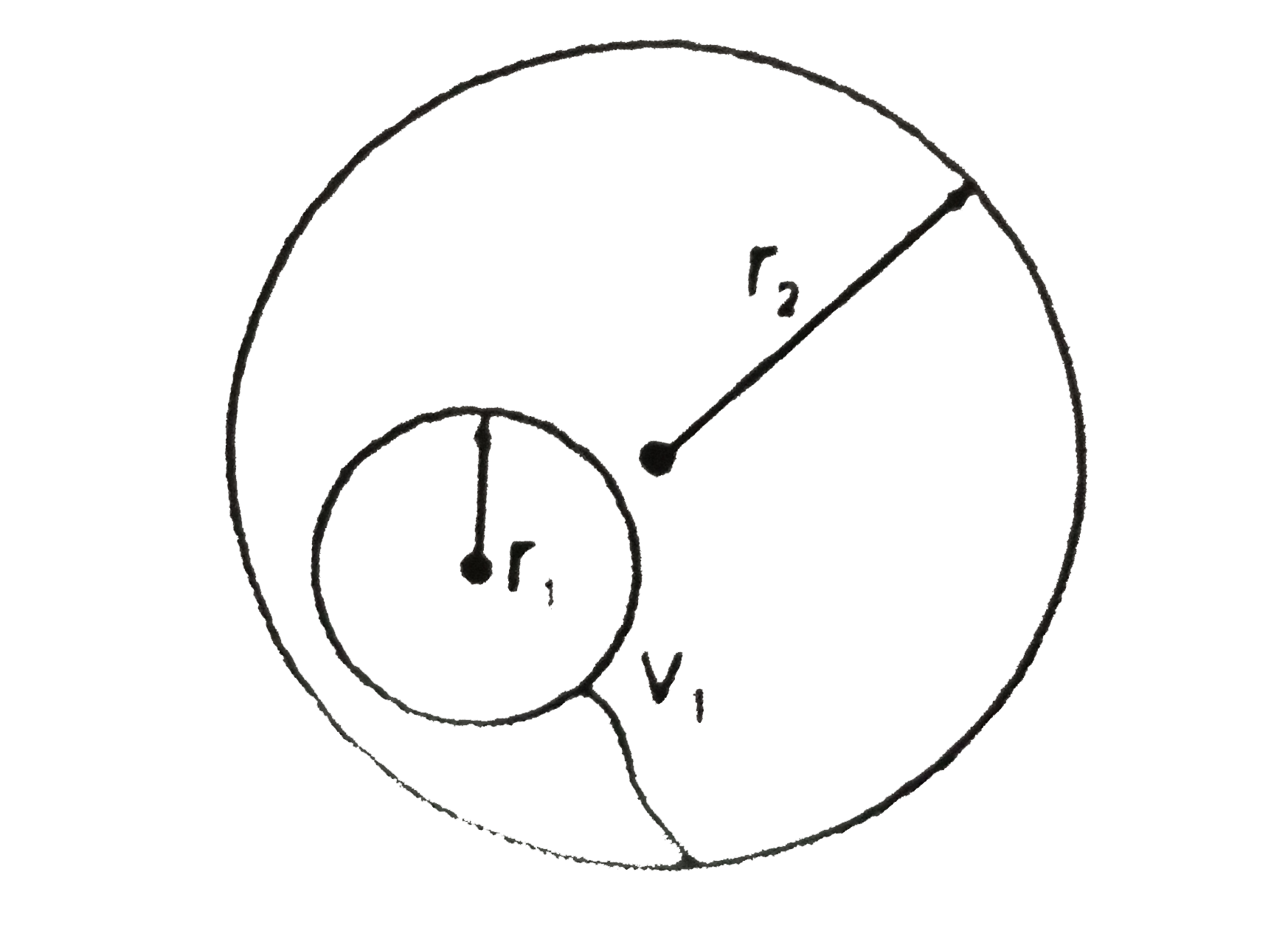
View SolutionA metal sphere of radius r1 charges to a potential V1 is then placed in a thin-walled uncharged conducting spherical shell of radius r2. Determine the potential acquired by the spherical shell after it has been connected for a short time to the sphere by a conductor.
View SolutionA hollow metal sphere of radius 10cm is charged such that the potential on its surface is 80 V. The potential at the centre of the sphere is
View SolutionA hollow metal sphere of radius 10cm is charged such that the potential on its surface is 80 V. The potential at the centre of the sphere is
View SolutionA hollow metal sphere of radius 5cm is charged so that the potential on its surface is 10V. The potential at the centre of the sphere is
View SolutionA common test to find the genotype of a hybrid is by
View SolutionA hollow metal sphere of radius 6 cm is charged such that the potential on its surface is 12 V.What is the potential at the centre of the sphere?
View Solution
