The cube shown in Fig. 2.119 has sides of length L=10.0cm . The electric field is uniform , has a magnitude E=4.00×103NC−1 and is parallel to the xy plane at an angle of 37∘ measured from the +x−aξs toward the +y−aξs .
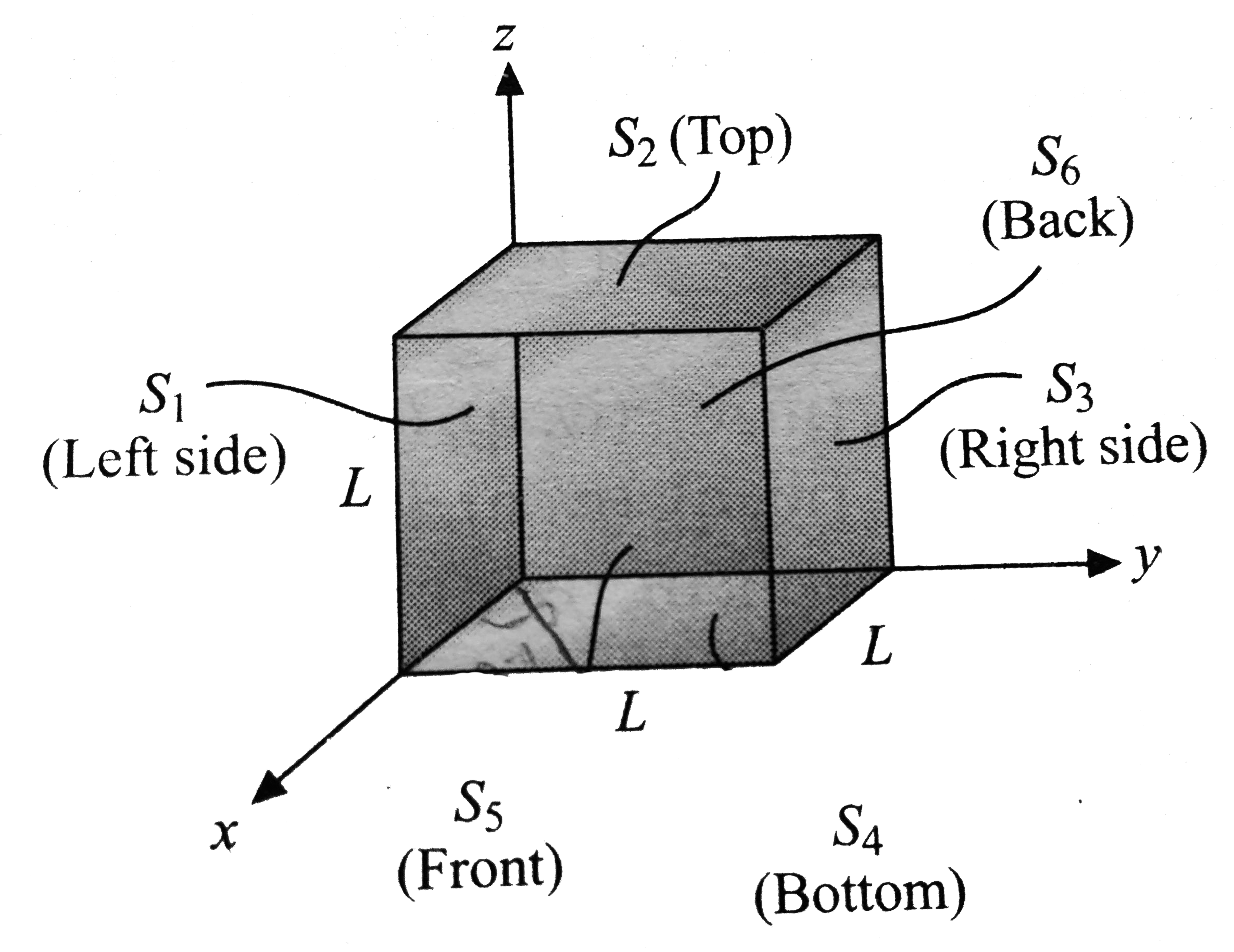
The surface that have zero flux are
S1 and S3
S5 and S6
S2 and S4
S1 and S1
The correct Answer is:C
Phi = vec(E ) . vec(A) = EA cos theta,where,vec(A) = A hat(n)<br>hat(n)_(S_(1) = - hat(j) (left),<br>Phi_(S_1))= -( 4 xx 10^(3) NC^(-1)) (0.1 m)^(2) cos (90^(@) - 37^(@)) = - 24 Nm^(2) C^(-1)<br> hat (n)_(S_(2)) = + hat(k)(⊤),<br>Phi_(S_(2)) = - (4 xx 10^(3) NC^(-1)) (0.1 m)^(2) cos 90^(@)=0
ˆnS3=+ˆj ( right),
ΦS3=+(4×103NC−1)(0.1m)2cos(90∘−37∘)
=+24Nm2C−1
ˆnS4=−ˆk (bottom),
ΦS4=(4×103NC−1)(0.1m)2cos90∘=0
ˆS5=+ˆi (front),
ΦS5=+4(4×103NC−1)(0.1m)2cos37∘=32Nm2C−1
ˆnS6=−ˆi (back),
ΦS6=−(4×103NC−1)(0.1m)2cos37∘=32Nm2C−1
ˆnS6=−(4×103NC−1)(0.1m)2cos37∘=−32Nm2C−1
As the field is uniform , the total flux through the cube must be zero , any flux entering the cube must also leave it.
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective type
7 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct
8 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
Similar Questions
The cube shown in Fig. 2.119 has sides of length L=10.0cm . The electric field is uniform , has a magnitude E=4.00×103NC−1 and is parallel to the xy plane at an angle of 37∘ measured from the +x−aξs toward the +y−aξs .

Electric flux passing through surface S1 is
View SolutionThe cube shown in Fig. 2.119 has sides of length L=10.0cm . The electric field is uniform , has a magnitude E=4.00×103NC−1 and is parallel to the xy plane at an angle of 37∘ measured from the +x−aξs toward the +y−aξs .

Electric flux passing through surface S6 is
View Solution
Knowledge Check
A circular plane sheet of radius 10 cm is placed in a uniform electric field of 5×105NC−1, making an angle of 60∘ with the field. Calculate electric flux through the sheet.
A1.36×102Nm2C−1B1.36×104Nm2C−1C0.515×102Nm2C−1D0.515×104Nm2C−1
The cube shown in Fig. 2.119 has sides of length L=10.0cm . The electric field is uniform , has a magnitude E=4.00×103NC−1 and is parallel to the xy plane at an angle of 37∘ measured from the +x−aξs toward the +y−aξs .

The total net electric flux through all faces of the cube is
View SolutionThe electric field in a region is given by →E=35E0→i+45E0→j with E0=2.0×103NC−1. Find the flux of this field through a recatngular surface of area 0.2m2 parallel to the y-z plane.
View SolutionThe electric field in a region is given by E=35E0ˆi+45E0j with E0=2.0×103N/C. Find the flux of this field through a rectangular surface of area 0.2m2 parallel to the y-z plane.
View SolutionA Charged particle of mass 1.0 g is suspended through a
. silk thread of length 40 cm in a horizantal electric field
. of 4.0×104NC−1 . If the particle stays aty a distance of
. 24 cm from the wall in equilibrium, find the charge on
. the particle.
View SolutionA cube has sides of length L=0.300m. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by →E=(−5.00NC−1)xˆi+(3.00NC−1)zˆk.
The total electric charge inside the cube is
View SolutionThe cube shown in, 50.0cm on a side, is in a uniform magnetic field of 0.120T, directed along the positive y-axis. Wires A,C,andD move in the direction indicated, each with a speed of 0.350ms−1. (Wire A moves parallel to the x-y plane, C moves at an angle of 45.0∘ below the x-y plane, and D moves parallel to the x-z plane.) What is the potential difference between the ends of each wire?

View SolutionA cube has sides of length L=0.300m. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by →E=(−5.00NC−1)xˆi+(3.00NC−1)zˆk.
The flux passing through the surface S5 will be
View Solution
