If Coulomb's law involved 1r3 (instead of 1r2), would Gauss's law still be true?
To determine whether Gauss's law would still hold true if Coulomb's law involved a 1r3 dependence instead of 1r2, we need to analyze the implications of this change step by step.
1. Understanding Coulomb's Law:
- Coulomb's law states that the electric force \( F \) between two point charges \( q_1 \) and \( q_2 \) separated by a distance \( r \) is given by:
\(
F = \frac{1}{4 \pi \epsilon_0} \frac{q_1 q_2}{r^2}
\)
- If we change this to \( \frac{1}{r^3} \), the force becomes:
\(
F = \frac{1}{4 \pi \epsilon_0} \frac{q_1 q_2}{r^3}
\)
2. Electric Field Calculation:
- The electric field \( E \) due to a point charge \( q \) is defined as the force per unit charge:
\(
E = \frac{F}{q} = \frac{1}{4 \pi \epsilon_0} \frac{q}{r^3}
\)
3. Applying Gauss's Law:
- Gauss's law states that the electric flux \( \Phi_E \) through a closed surface is proportional to the charge enclosed \( Q \):
\(
\Phi_E = \oint E \cdot dS = \frac{Q_{\text{enc}}}{\epsilon_0}
\)
- For a spherical surface of radius \( r \) surrounding a charge \( q \), the electric field \( E \) would be uniform over the surface.
4. Calculating the Electric Flux:
- The area \( A \) of a sphere is \( 4\pi r^2 \), so the electric flux through the surface is:
\(
\Phi_E = E \cdot A = E \cdot 4\pi r^2
\)
- Substituting \( E \):
\(
\Phi_E = \left(\frac{1}{4 \pi \epsilon_0} \frac{q}{r^3}\right) \cdot 4\pi r^2
\)
- Simplifying this gives:
\(
\Phi_E = \frac{q}{\epsilon_0 r}
\)
5. Comparison with Gauss's Law:
- According to Gauss's law, the flux should be:
\(
\Phi_E = \frac{Q_{\text{enc}}}{\epsilon_0} = \frac{q}{\epsilon_0}
\)
- However, we found that:
\(
\Phi_E = \frac{q}{\epsilon_0 r}
\)
- This indicates that the electric flux depends on the radius \( r \), which contradicts Gauss's law.
6. Conclusion:
- Since the electric flux derived from the modified Coulomb's law depends on the distance \( r \), Gauss's law would not hold true in this scenario.
Final Answer:
No, Gauss's law would not be true if Coulomb's law involved 1r3 instead of 1r2.
- Coulomb's law states that the electric force \( F \) between two point charges \( q_1 \) and \( q_2 \) separated by a distance \( r \) is given by:
\(
F = \frac{1}{4 \pi \epsilon_0} \frac{q_1 q_2}{r^2}
\)
- If we change this to \( \frac{1}{r^3} \), the force becomes:
\(
F = \frac{1}{4 \pi \epsilon_0} \frac{q_1 q_2}{r^3}
\)
- The electric field \( E \) due to a point charge \( q \) is defined as the force per unit charge:
\(
E = \frac{F}{q} = \frac{1}{4 \pi \epsilon_0} \frac{q}{r^3}
\)
- Gauss's law states that the electric flux \( \Phi_E \) through a closed surface is proportional to the charge enclosed \( Q \):
\(
\Phi_E = \oint E \cdot dS = \frac{Q_{\text{enc}}}{\epsilon_0}
\)
- For a spherical surface of radius \( r \) surrounding a charge \( q \), the electric field \( E \) would be uniform over the surface.
- The area \( A \) of a sphere is \( 4\pi r^2 \), so the electric flux through the surface is:
\(
\Phi_E = E \cdot A = E \cdot 4\pi r^2
\)
- Substituting \( E \):
\(
\Phi_E = \left(\frac{1}{4 \pi \epsilon_0} \frac{q}{r^3}\right) \cdot 4\pi r^2
\)
- Simplifying this gives:
\(
\Phi_E = \frac{q}{\epsilon_0 r}
\)
- According to Gauss's law, the flux should be:
\(
\Phi_E = \frac{Q_{\text{enc}}}{\epsilon_0} = \frac{q}{\epsilon_0}
\)
- However, we found that:
\(
\Phi_E = \frac{q}{\epsilon_0 r}
\)
- This indicates that the electric flux depends on the radius \( r \), which contradicts Gauss's law.
- Since the electric flux derived from the modified Coulomb's law depends on the distance \( r \), Gauss's law would not hold true in this scenario.
No, Gauss's law would not be true if Coulomb's law involved 1r3 instead of 1r2.
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.2
14 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective
12 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Example
7 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
Similar Questions
If magnetic monpole existed, how would Gauss law of magnetism be modified?
View SolutionCoulomb's law states that the electric force becomes weaker with increasing distance. Suppose that instead, the electric force between two charged particles were independent of distance. In this case, would a neutral insulator still be attracted towards the comb.
View Solution
Knowledge Check
The Bohr model for the H-atom relies on the Coulomb's law of electrostatics . Coulomb's law has not directly been varified for very short distances of the order of angstroms. Suppos-ing Coulomb's law between two oppsite charge +q1,−q2 is modified to ∣∣→F∣∣=q1q2(4πε0)r21r2,r≥R0
=q1q2(4πε0)r21R20(R0r)ε,r≤R0
Calculate in such a case , the ground state enenergy of H-atom , if ε=0.1,R0=1ÅA−11.4B−17.3C5.9D−23.2If the gravitational force had varied as r−5/2 instead of r−2 the potential energy of a particle at a distance 'r' from the centre of the earth would be proportional to
Ar−1Br−2Cr−3/2Dr−5/2Which of the following statements is not true about Gauss's law?
AGauss's law is true for any closed surface.BThe term q on the ringht side of Gauss's law includes the sum of all charges enclosed by the surface.CGauss's law is not much useful in calculating electrostatic field when the system has some symmetry.DGauss's law is based on the inverse square dependence on distance contained in the coulomb's law.
Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss's law. [Hint.use Coulomb's law directly and evaluate the necessary integral ].
View SolutionA: Raoult's law applicable for dilute solution only.
R: Henry's law is applicable for solution of gas in liquid.
View SolutionWhat is the nature of Gaussian surface involved in Gauss's law of electrostatics?
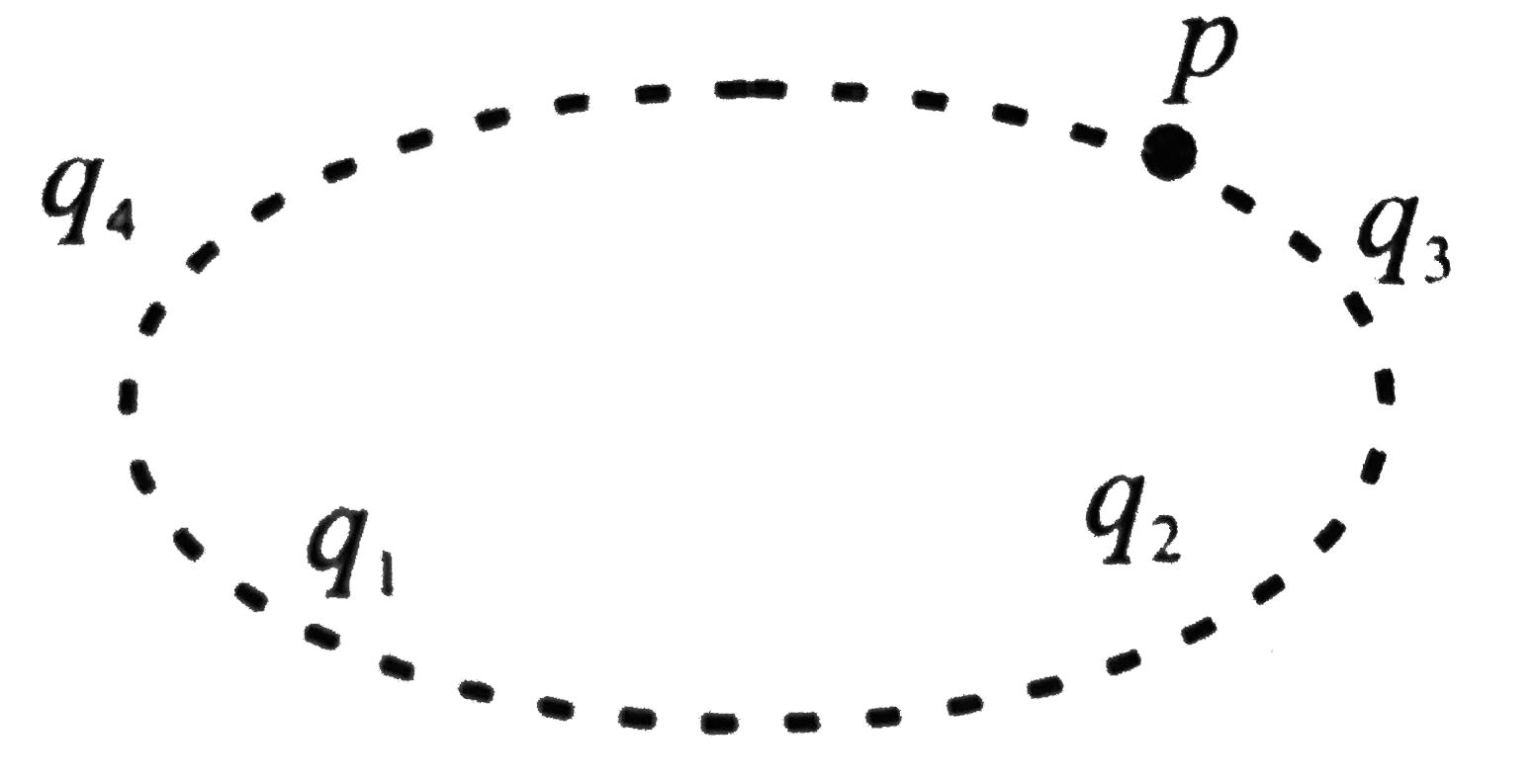
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
The net flux of the electric field through the surface due to q3 and q4 is
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
A Gaussian surface encloses two of the four positively charged particles. The particles that contribute to the electric field at a point P on the surface are
View Solution
