Four identical point charges are placed at the corners of a square, A fifth point charge placed at the center of the square experiences zero net force . Is this a stable equilirium for the fifth charge? Explain.
To determine if the fifth point charge placed at the center of the square experiences stable equilibrium, we need to analyze the forces acting on it when it is slightly displaced from the center.
1. Understanding the Setup:
- We have four identical point charges located at the corners of a square.
- A fifth point charge is placed at the center of the square.
2. Net Force at the Center:
- Due to symmetry, the forces exerted by the four corner charges on the fifth charge at the center cancel each other out.
- Therefore, the net force acting on the fifth charge at the center is zero. This means the charge is in equilibrium.
3. Displacement from the Center:
- Now, consider displacing the fifth charge slightly from the center towards one of the corners.
- The charge will experience forces from the corner charges that are no longer balanced.
4. Analyzing the Forces:
- If the charge is displaced towards a corner, the distance to that corner charge decreases, increasing the force exerted by that charge on the fifth charge.
- Simultaneously, the distances to the other three corner charges increase, decreasing the forces exerted by them.
5. Direction of the Resultant Force:
- The net force will now point away from the center towards the corner that the charge is displaced towards.
- This means that if the fifth charge is displaced, it will experience a force that pushes it further away from the center.
6. Conclusion on Stability:
- Since the net force acts in the direction away from the equilibrium position (the center), the equilibrium is unstable.
- If the fifth charge is slightly displaced, it will not return to the center but will move further away, confirming that the equilibrium is unstable.
Final Answer:
The fifth point charge placed at the center of the square does not experience stable equilibrium. When displaced from the center, it experiences a net force that pushes it further away from the equilibrium position, indicating instability.
- We have four identical point charges located at the corners of a square.
- A fifth point charge is placed at the center of the square.
- Due to symmetry, the forces exerted by the four corner charges on the fifth charge at the center cancel each other out.
- Therefore, the net force acting on the fifth charge at the center is zero. This means the charge is in equilibrium.
- Now, consider displacing the fifth charge slightly from the center towards one of the corners.
- The charge will experience forces from the corner charges that are no longer balanced.
- If the charge is displaced towards a corner, the distance to that corner charge decreases, increasing the force exerted by that charge on the fifth charge.
- Simultaneously, the distances to the other three corner charges increase, decreasing the forces exerted by them.
- The net force will now point away from the center towards the corner that the charge is displaced towards.
- This means that if the fifth charge is displaced, it will experience a force that pushes it further away from the center.
- Since the net force acts in the direction away from the equilibrium position (the center), the equilibrium is unstable.
- If the fifth charge is slightly displaced, it will not return to the center but will move further away, confirming that the equilibrium is unstable.
The fifth point charge placed at the center of the square does not experience stable equilibrium. When displaced from the center, it experiences a net force that pushes it further away from the equilibrium position, indicating instability.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Solved examples
Explore 10 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Exercises
Explore 58 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
Similar Questions
Knowledge Check
Four charges are arranged at the corners of a square ABCD, as shown in the adjoining figure. The force on the charge kept at the centre O is
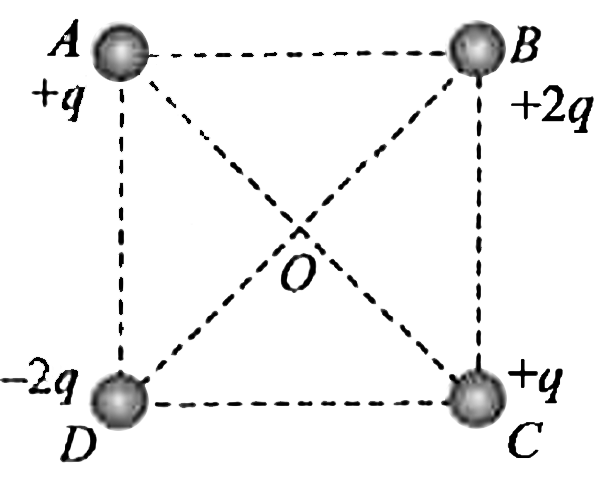 Aalong the diagonal BDBalong the diagonal ACCzeroDperpendicular to side AB
Aalong the diagonal BDBalong the diagonal ACCzeroDperpendicular to side AB
Four identical charges each .q. are placed at four corners of a square of side .a.. Find the charge to be placed at the centre of the square so that the system of charges is in equilibrium
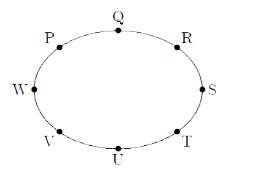
View SolutionA planet travels in an elliptical orbit about a star as shown. At what pair of points is the speed of the planet the same?
View SolutionA point charge Q is placed at the corner of a square of side a. Find the flux through the square.
View SolutionFour point charges are placed at the corners of a square ABCD of side 10 cm, as shown in figure. The force on a charge of 1μC placed at the centre of square is

View SolutionFour identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
 .
.
View SolutionFour charges are arranged at the corners of a square as shown in the figure. The direction of electric field at the centre of the square is along

View SolutionFour positive charges (2√2−1)Q are arranged at the four corners of a square. Another charge q is placed at the centre of the square. Resulting force acting on each corner charge is zero if q is
View Solution


 .
.