A hollow sphere is completely filled with a liquid having a density ρ. The radius of the sphere is R. Now the sphere is puloled with a constant horizontal acceleration of g on a horizontal surface. Take centre of sphere as origin of coordinate system as shown in the figure. 
Coordinate of the point having the maximum pressure is
R√2,R√2
R2,R2
−R√2,−R√2
−R2,−R2
The correct Answer is:c
Effective gravity (√2g) will be along line OC.
Pressure will be minimum at D and maximum at c.
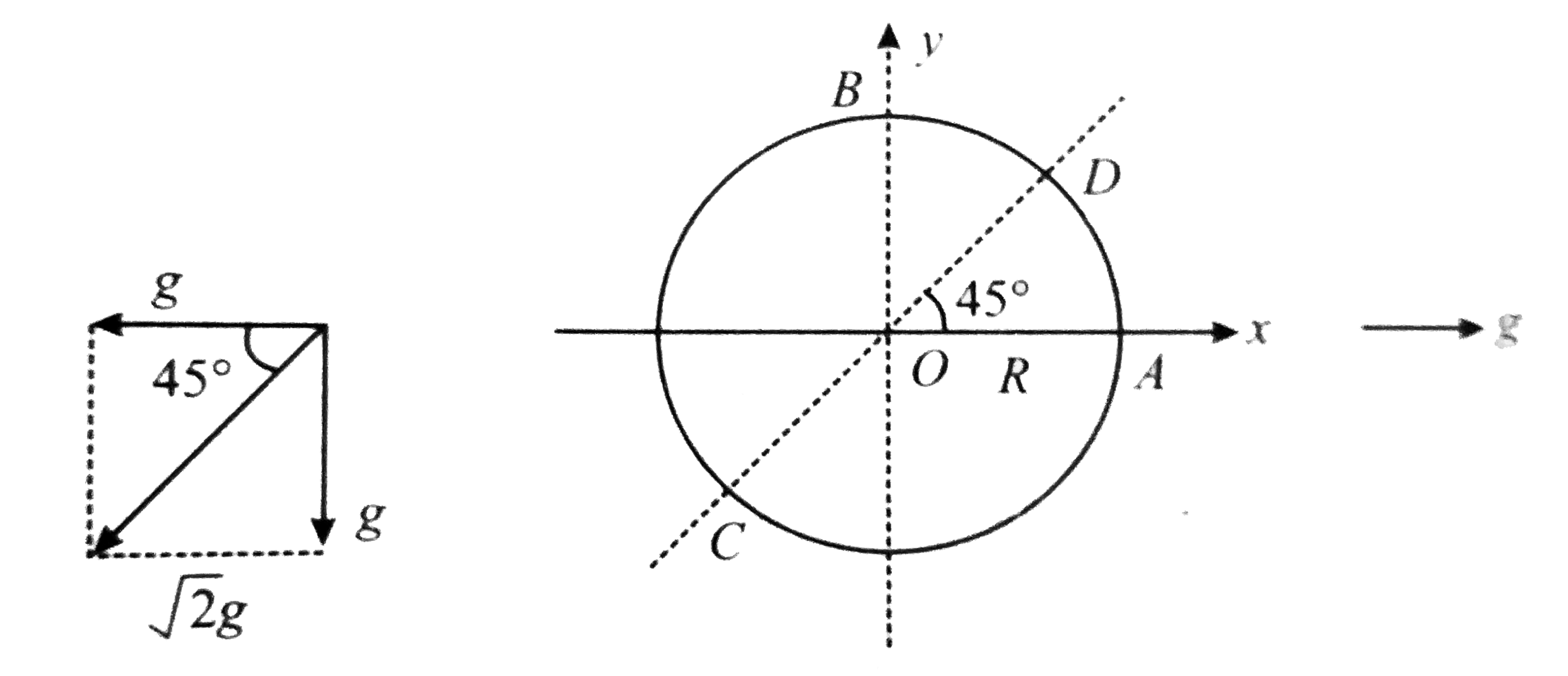
Pressure will be the same at all points on a surface which is perpendicular to line CD. Hence PA=PB
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - MCQ_TYPE
20 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
Similar Questions
A hollow sphere is completely filled with a liquid having a density ρ. The radius of the sphere is R. Now the sphere is puloled with a constant horizontal acceleration of g on a horizontal surface. Take centre of sphere as origin of coordinate system as shwon in the figure.

Coordinate of the point having the minimum pressure is
View SolutionA hollow sphere is completely filled with a liquid having a density ρ. The radius of the sphere is R. Now the sphere is puloled with a constant horizontal acceleration of g on a horizontal surface. Take centre of sphere as origin of coordinate system as shown in the figure.

Consider points A and B as shown in the figure.
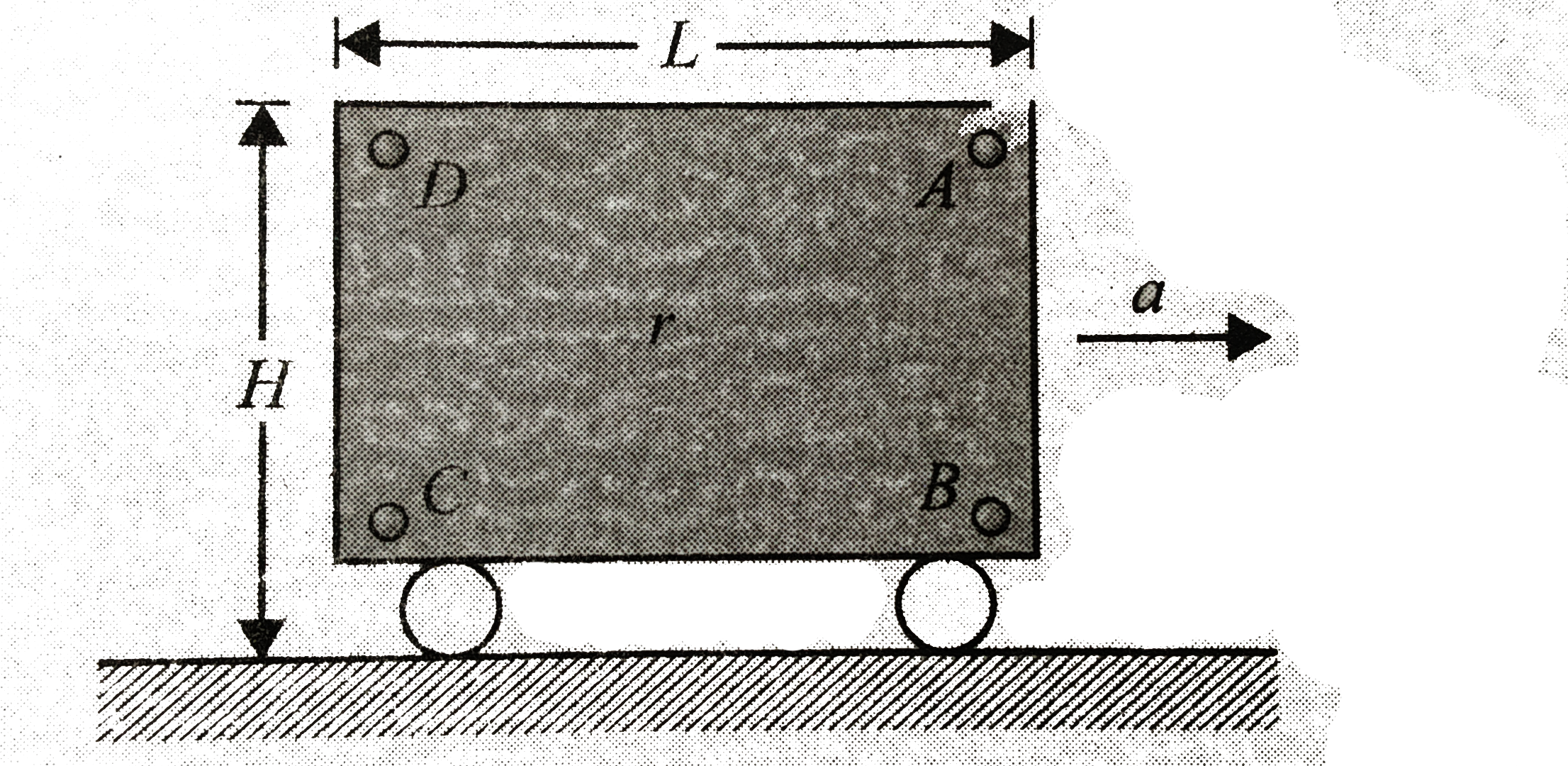
View SolutionA rectangular box is completely filled with a liquid of density ρ, as shown in Fig. The box is accelerated horizontally with a constant acceleration a. Determine the gauge pressures at the four points A,B,C and D.
View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is

View SolutionA thin hollow sphere of mass m is completely filled with a liquid of mass m. When the sphere rolls with a velocity v kinetic energy of the system is (neglect friction)
View SolutionA solid sphere rolling on a rough horizontal surface. Acceleration of contact point is zero.
A solid sphere can roll on the smooth surface.
View SolutionA small body of mass 'm' is placed at the top of a smooth sphere of radius 'R' placed on a horizontal surface as shown, Now the sphere is given a constant horizontal acceleration a0=g. The velocity of the body relative to the sphere at the moment when it loses contact with the sphere is

View SolutionA nonconducting sphere of radius R is filled with uniform volume charge density −ρ. The center of this sphere is displaced from the origin by →d. The electric field →E at any point P having position vector inside the sphere is

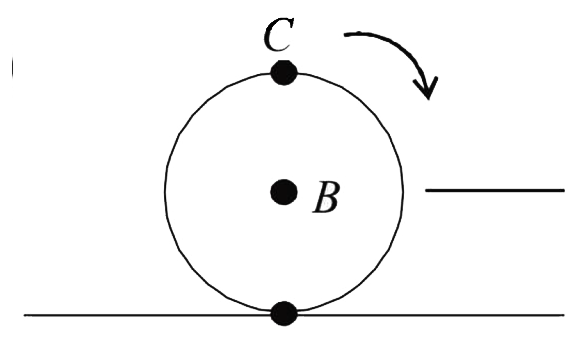
View SolutionA sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then
View SolutionAssuming the earth to be a homogeneous sphere of radius R, its density in terms of G (constant of gravitation) and g (acceleration due to gravity on the surface of the earth)
View Solution
