Assume the radius of the earth to be $6.4 \times 10^{6} m$
a. Calculate the time period $T$ of a satellite on equational orbit at $1.4 \times 10^{e} m$ above the surface of the earth.
b. What is the speed of the satellite in this orbit?
c. If the satellite is travelling in the same direction as the rotation of the earth i.e. west to east, what is the interval between two successie times at which it will appear vertically overhead to an observed at a fixed point on the equator?

Video Solution

Text Solution

Verified by Experts

a. $r = R_{earth} + h = 6.4 \times 10^{6} + 1.4 \times 10^{6} = 7.8 \times 10^{6} m$
$\Rightarrow r = 7.8 \times 10^{6} m \Rightarrow T = (\frac{4 π^{2} r^{3}}{G M_{earth}}) = 6831 s$
b. Speed of satellite
$V = \sqrt{\frac{G M_{earth}}{r}} = 7174 m s^{- 1}$
c. Relative angular velocity $= ω_{satellite} - ω_{earth}$
Thus $T = \frac{2 π}{ω_{s} - ω_{e}} = \frac{2 π}{[\frac{2 π}{T_{s}} - \frac{2 π}{T_{e}}]}$
$\Rightarrow T = \frac{T_{s} T_{e}}{T_{e} - T_{s}} = 7471 s$

Updated on:21/07/2023

Match the Column I with Column II
For a satellite in circular orbit

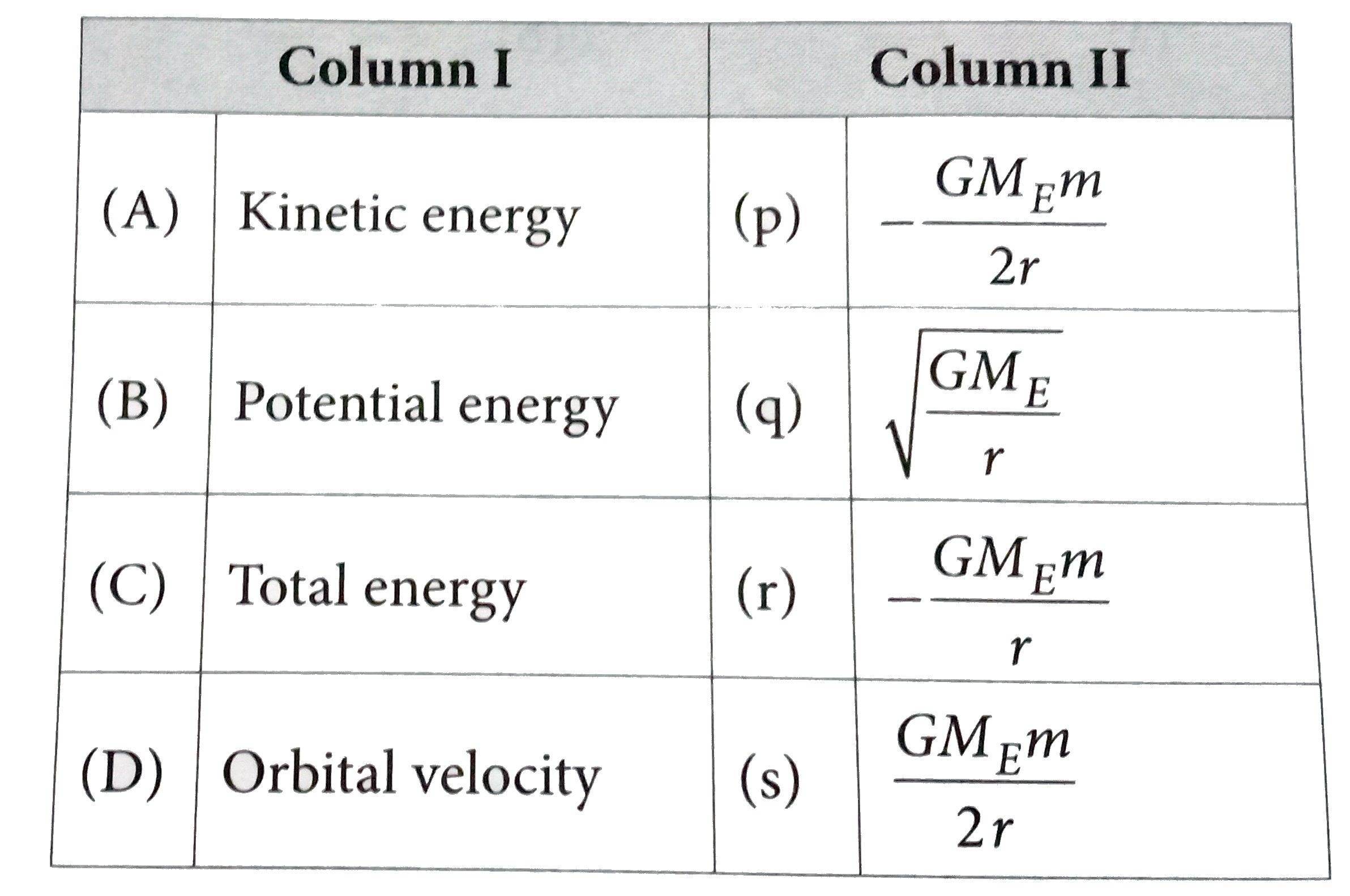
(where $M_{E}$ is the mass of the earth , m is the mass of the satellite and r is the radius of the orbit )
AA-r, B-s,C-q,D-p
BA-q,B-p,C-r,D-s
CA-p,B-q,C-s,D-r
DA-s,B-r,C-p,D-q
A geostationary satellite is orbiting the earth at a height of 6R above the surface of the earth, where R is the radius of the earth. The time period of another satellite at a height of 2.5 R from the surface of the earth is …… hours.
A $3 \sqrt{2} h$
B $1.5 \sqrt{2} h$
C $6 \sqrt{2} h$
D $12 \sqrt{2} h$