A vessel whose , bottom has round holes with diameter 0.1mm, is filled with water. The maximum height up to which water can be filled without leakage is
100cm
75cm
50cm
30cm
The correct Answer is:D
To find the maximum height up to which water can be filled in a vessel with a hole at the bottom, we can use the principles of fluid mechanics, specifically the relationship between pressure, surface tension, and the geometry of the hole.
1. Understand the Problem:
We have a vessel with a hole at the bottom, and we need to determine the maximum height of water that can be filled without leaking out through the hole.
2. Identify Given Data:
- Diameter of the hole, d=0.1mm=0.1×10−3m=1×10−4m
- Radius of the hole, R=d2=1×10−42=0.5×10−4m
- Density of water, ρ≈1000kg/m3
- Acceleration due to gravity, g≈9.8m/s2
- Surface tension of water, T≈0.072N/m
3. Apply the Pressure Balance:
The pressure at the bottom of the vessel due to the height of the water column must balance the pressure drop due to surface tension at the hole. The pressure at the bottom is given by:
P=Patm+ρgh
The pressure drop due to surface tension at the hole can be expressed as:
ΔP=2TR
Setting these equal gives:
ρgh=2TR
4. Rearranging for Height:
We can rearrange the equation to solve for h:
h=2TρgR
5. Substituting Values:
Substitute the known values into the equation:
h=2×0.0721000×9.8×(0.5×10−4)
6. Calculating:
First calculate the denominator:
1000×9.8×(0.5×10−4)=1000×9.8×0.000005=0.049
Now substitute back:
h=0.1440.049≈2.94m
7. Final Result:
The maximum height up to which water can be filled without leakage is approximately 2.94m.
We have a vessel with a hole at the bottom, and we need to determine the maximum height of water that can be filled without leaking out through the hole.
- Diameter of the hole, d=0.1mm=0.1×10−3m=1×10−4m
- Radius of the hole, R=d2=1×10−42=0.5×10−4m
- Density of water, ρ≈1000kg/m3
- Acceleration due to gravity, g≈9.8m/s2
- Surface tension of water, T≈0.072N/m
The pressure at the bottom of the vessel due to the height of the water column must balance the pressure drop due to surface tension at the hole. The pressure at the bottom is given by:
P=Patm+ρgh
The pressure drop due to surface tension at the hole can be expressed as:
ΔP=2TR
Setting these equal gives:
ρgh=2TR
We can rearrange the equation to solve for h:
h=2TρgR
Substitute the known values into the equation:
h=2×0.0721000×9.8×(0.5×10−4)
First calculate the denominator:
1000×9.8×(0.5×10−4)=1000×9.8×0.000005=0.049
Now substitute back:
h=0.1440.049≈2.94m
The maximum height up to which water can be filled without leakage is approximately 2.94m.
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Multiple Correct
Explore 17 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Assertion- Reasoning
Explore 13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Subjective
Explore 16 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
Similar Questions
A vessel, whose bottom has round holes with diameter of 0.1 mm , is filled with water. The maximum height to which the water can be filled without leakage is (S.T. of water =75 dyne/cm , g=1000 cm/s)
View SolutionA vessel whose bottom has round holes with a diameter of d=0.1mm is filled with water. The maximum height of the water level h at which the water does not flow out, will be (The water does not wet the bottom of the vessel). [STofwater=70dyne/cm]
View SolutionA vessel whose bottom has round holes with diameter of 1 mm is filled with water Assuming that surface tension acts only at holes, then the maximum height to which the water can be filled in vessel without leakage is (given surface tension of water is 75×10−3N/m) and g=10m/s2
View SolutionA cylindrical tank has a hole of 1cm2 in its bottom. If the water is allowed to flow into the tank from a tube above it at the rate of 70cm3/sec, then the maximum height up to which water can rise in the tank is
View SolutionA cylindrical tank has a hole of 1cm2 in its bottom. If the water is allowed to flow into the tank from a tube above it at the rate of 70cm3/sec, then the maximum height up to which water can rise in the tank is
View SolutionA cylinderical tank of height 0.4 m is open at the top and has a diameter 0.16m. Water is filled in it up to height of 0.16 m. Find the time taken to empty the tank through a hole of radius 5×10−3m in its bottom.
View SolutionA container of height 10 cm is filled with water. There is hole at bottom. Find the pressure difference between point A & B .
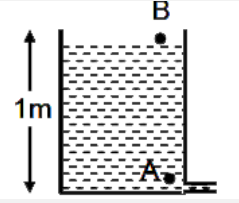
View SolutionA wide vessel with a small hole in the bottom is filled with water and kerosene. Find the velocity of water flow if the thickness of water layer is h1=30cm and that of kerosene is h2=20cm brgt

View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the minimum value of height h1 (in situation 1), for which the block just starts to move up?
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the minimum value of height h1 (in situation 1), for which the block just starts to move up?
View Solution

