A force of 3.14N is required to drag a sphere of radius 4cm with a speed of 5ms−1 in a medium in gravity free space. Find the coefficient of the viscosity of the medium.
To find the coefficient of viscosity of the medium, we can use the formula for the drag force acting on a sphere moving through a viscous medium:
F=6πμrv
Where:
- F is the drag force (in Newtons),
- μ is the coefficient of viscosity (in poise),
- r is the radius of the sphere (in centimeters),
- v is the velocity of the sphere (in centimeters per second).
Step 1: Convert the radius to centimeters
The radius of the sphere is given as 4cm, which is already in the correct unit.
Step 2: Convert the velocity to centimeters per second
The velocity is given as 5m/s. To convert this to centimeters per second:
v=5m/s×100cm/m=500cm/s
Step 3: Substitute the values into the formula
We know:
- F=3.14N
- r=4cm
- v=500cm/s
Now we can rearrange the formula to solve for μ:
μ=F6πrv
Step 4: Substitute the known values into the rearranged formula
Substituting the values we have:
μ=3.146×π×4×500
Step 5: Calculate the denominator
Calculating the denominator:
6×π≈6×3.14=18.84
Then:
18.84×4=75.36
And:
75.36×500=37680
Step 6: Calculate the viscosity
Now substituting back into the equation:
μ=3.1437680
Calculating this gives:
μ≈8.3×10−5poise
Final Answer
The coefficient of viscosity of the medium is approximately:
μ≈8.3×10−5poise
---
- F is the drag force (in Newtons),
- μ is the coefficient of viscosity (in poise),
- r is the radius of the sphere (in centimeters),
- v is the velocity of the sphere (in centimeters per second).
The radius of the sphere is given as 4cm, which is already in the correct unit.
The velocity is given as 5m/s. To convert this to centimeters per second:
v=5m/s×100cm/m=500cm/s
We know:
- F=3.14N
- r=4cm
- v=500cm/s
μ=F6πrv
Substituting the values we have:
μ=3.146×π×4×500
Calculating the denominator:
6×π≈6×3.14=18.84
Then:
18.84×4=75.36
And:
75.36×500=37680
Now substituting back into the equation:
μ=3.1437680
Calculating this gives:
μ≈8.3×10−5poise
The coefficient of viscosity of the medium is approximately:
μ≈8.3×10−5poise
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.3
9 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Subjective
16 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.1
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
An electorn moves in a circle of radius 10cm with a constant speed of 4.0×106ms−1.Find the electric current at a point on the circle.
View SolutionElectromagnetic travel in a medium at a speed of 2.0×108ms−1. The relative permitivity of the medium is 2.25. Find the relative permeability of the medium.
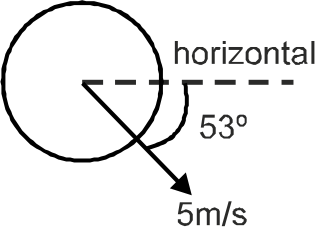
View SolutionAn external force 6N is applied on a sphere of radius R = 10 cm of mass 1 kg and the sphere moves in a liquid with a constant velocity 5 m/s making 530 with the horizontal.The coefficient of viscosity of the liquid is 20/(6π), in S.I units. (Take g=10m/s2)
View SolutionWater from a hosepipe of radius 5 cm strikes a wall at a speed of 5ms−1 normally and stops. The force exerted on the wall in newton is
View SolutionA sphere of mass m and radius r is projected in a gravity free space with speed v. If coefficient of viscosity of the medium in which it moves is 16π , the distance travelled by the body before it stops is
View SolutionA sphere of mass m and radius r is projected in a gravity free space with speed v. If coefficient of viscosity of the medium in which it moves is 16π , the distance travelled by the body before it stops is
View Solution
A space 2.5cm wide between two large plane surfaces is filled with oil. Force required to drag a very thin plate of area 0.5m2 just midway the surfaces at a speed of 0.5msec is 1N. The coefficient of viscosity in kg−sm2 is:
View SolutionFind the surface area of a sphere of radius: 10.5 cm (ii) 5.6 cm (iii) 14 cm
View SolutionFind the surface area of a sphere of radius: 10.5 cm (ii) 5.6 cm (iii) 14 cm
View SolutionFind the surface area of a sphere of radius:(i) 10.5 cm (ii) 5.6 cm (iii) 14 cm
View Solution
