A sphere of radius 10cm and mass 25 kg is attached to the lower end of a steel wire of length 5m and diameter 4mm which is suspended from the ceiling of a room . The point of support is 521cm above the floor. When the sphere is set swinging as a simple pendulum, its lowest point just grazes the floor. Calculate the velocity of the ball at its lowest position (Ysteel=2×1011N/m2).
Young's modulus of steel=20×1010N/m2
Unstretched length of the wire =500cm
Radius of the steel wire =0.05cm
A wire can be considered as a spring of suitable force constant. For a wire
Y=FA△l/l=FLA△l⇒F=YAll△l
Now F=k.△l
Therefore k (force cosnant =F△l=YAl
⇒k=20×1010×π(0.05×10−2)25=π×10N/m2
Now we may treat the problem as if the mass were suspended by a spring of force constant k=104πN/m2. Considering the dynamics of circular motion at the lowest point
T−mg=mv2r
Obviously, at the lowest point the wire elongates by 1cm
∴T=k△l=π×104×0.01=π×102N
∴π×102−25×9.8=25×v25.21
v2=(100π−245)×5.2125=14.42
⇒v=3.8ms−1
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.1
12 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.2
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
A sphere of radius 0.1m and mass 8πkg is attached to the lower end of a steel wire of length 5.0m and diameter 10−3. The wire is suspended from 5.22m high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position . Young's modulus of steel is (1.994×1011N/m2).
View SolutionA solid sphere of radius 1cm is melted to stretch into a wire of length 100 cm. Find the radius of the wire.
View Solution
Knowledge Check
A 14.5 kg mass, fastened to the end of a steel wire of unstretched length 1m, is whirled in a vertical circle with an angular velocity of 2rev./s at the bottom of the circle. The cross-sectional area of the wire is 0.065cm2 . Calculate the elongation of the wire when the mass is at the lowest point of its path Ysteel=2×1011Nm−2.
A0.52 mmB1.52 mmC2.52 mmD3.52 mm
A sphere of mass 10 kg and radius 0.5 m rotates about a tangent. The moment of inertia of the sphere is
View SolutionA steel wire 2m long is suspended from the ceiling. When a mass is hung from its lower end, the increase in length recorded is 1cm. Determine the strain in the wire.
View SolutionA steel wire of length 4 m and diameter 5 mm is strethed by 5 kg-wt. Find the increase in its length, if the Young's modulus of steel is 2×1012 dyne cm2
View SolutionA sphere of mass 3 kg is attached to one end of a steel wire of length 1 m and radius 1mm. It is whirled in a vertical circle with an angular velocity of 2 rev / s. What is the elongation of the wire, when the weight is at the lowest point of its path? Y for steel =20×1010N/m2.
View SolutionWhen a weight of 5kg is suspended from a copper wire of length 30m and diameter 0.5mm, the length of the wire increases by 2.4cm. If the diameter is doubled, the extension produced is
View SolutionA 14.5 kg mass, fastened to the end of a steel wire of unstretched length 1m, is whirled in a vertical circle with an angular velocity of 2rev./s at the bottom of the circle. The cross-sectional area of the wire is 0.065cm2 . Calculate the elongaton of the wire when the mass is at the lowest point of its path Ysteel=2×1011Nm−2.
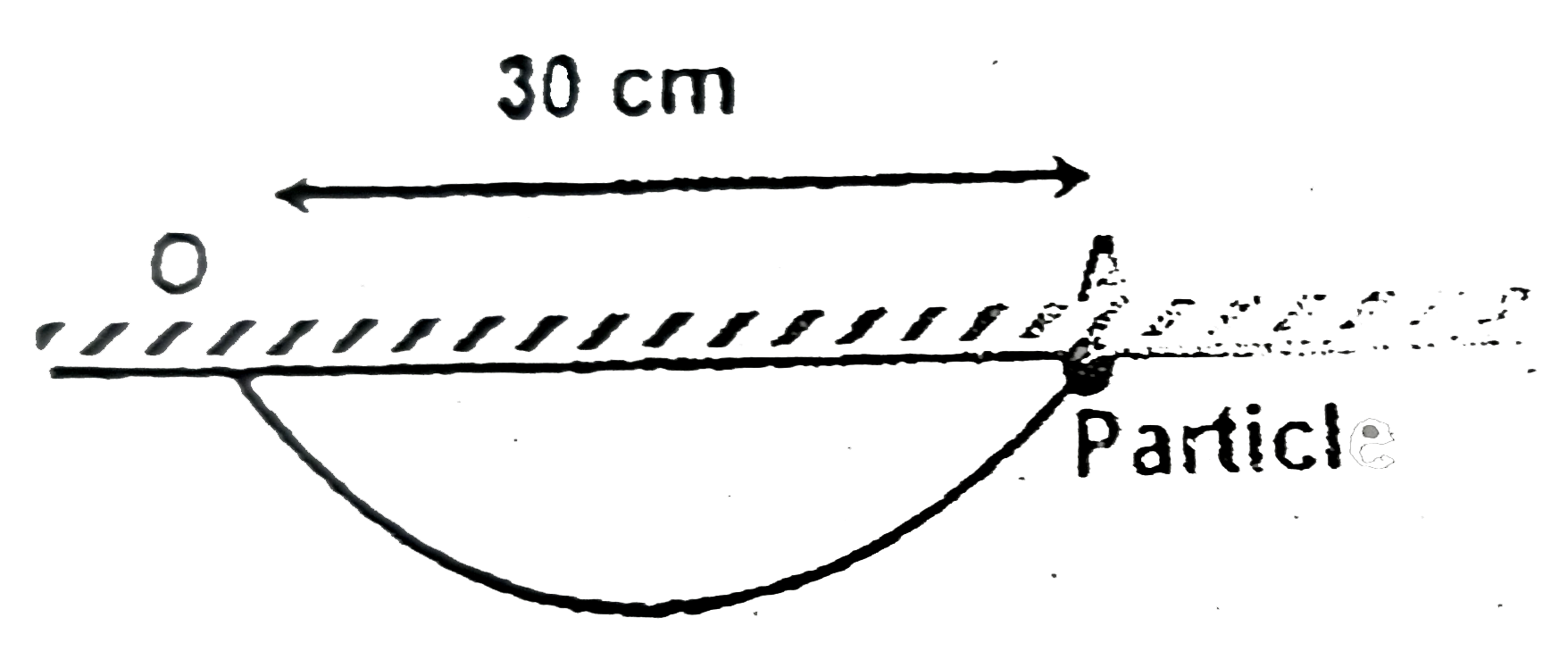
View SolutionA small ball of mass 100g is attached to a light and inextensible string of length 50cm. The string is tied to a support O and the mass m released from point A which is a' a horizontal distance of 30cm from the support. Calculate the speed of the ball is its lowest point of the trajectory.
View Solution
