Question

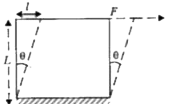
Two parallel and opposite forces, each of magnitude $4000N$, are applied tangentially to the upper and lower faces of a cubical metal block $25cm$ on a side. Find the angle of shear and the displacement of the upper surface relative to the lower surface. The shear modulus for the metal is $80GPa$.

Explanation

To solve the problem, we will follow these steps:

Step 1: Understand the Given Information
- Two parallel and opposite forces, each of magnitude \( F = 4000 \, \text{N} \).
- The side length of the cubical metal block \( L = 25 \, \text{cm} = 0.25 \, \text{m} \).
- Shear modulus \( G = 80 \, \text{GPa} = 80 \times 10^9 \, \text{N/m}^2 \).

Step 2: Calculate the Area of the Faces
The area \( A \) of one face of the cube is given by:
\( A = L^2 = (0.25 \, \text{m})^2 = 0.0625 \, \text{m}^2 \)

Step 3: Calculate Shear Stress
Shear stress \( \tau \) is defined as the force per unit area:
\( \tau = \frac{F}{A} = \frac{4000 \, \text{N}}{0.0625 \, \text{m}^2} = 64000 \, \text{N/m}^2 \)

Step 4: Calculate the Angle of Shear
The angle of shear \( \phi \) can be calculated using the formula:
\( \phi = \frac{\tau}{G} \)
Substituting the values:
\( \phi = \frac{64000 \, \text{N/m}^2}{80 \times 10^9 \, \text{N/m}^2} = 8 \times 10^{-7} \, \text{radians} \)

Step 5: Calculate the Displacement of the Upper Surface
The displacement \( \Delta l \) of the upper surface relative to the lower surface can be calculated using:
\( \phi = \frac{\Delta l}{L} \)
Thus, rearranging gives:
\( \Delta l = \phi \times L \)
Substituting the values:
\( \Delta l = (8 \times 10^{-7} \, \text{radians}) \times (0.25 \, \text{m}) = 2 \times 10^{-7} \, \text{m} = 2 \times 10^{-5} \, \text{cm} \)

Final Answers
- Angle of Shear: \( \phi = 8 \times 10^{-7} \, \text{radians} \)
- Displacement: \( \Delta l = 2 \times 10^{-5} \, \text{cm} \)