A small block of mass 4kg is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius of 5m about the hole, with a tangential velocity of 4m/s. The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is 200N.
Velocity of the block at the time of breaking of the string
10m/s
20m/s
7.5m/s
12.5m/s
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Understand the conservation of angular momentum
The angular momentum of the block must remain constant since there are no external torques acting on it. The initial angular momentum L1 is given by:
L1=m⋅v1⋅r1
where:
- m=4kg (mass of the block)
- v1=4m/s (initial tangential velocity)
- r1=5m (initial radius)
Step 2: Calculate the initial angular momentum
Substituting the values into the equation:
L1=4kg⋅4m/s⋅5m=80kg m2/s
Step 3: Set up the equation for final angular momentum
When the radius is shortened to r2 and the velocity becomes v2, the final angular momentum L2 is:
L2=m⋅v2⋅r2
Since angular momentum is conserved, we have:
L1=L2⟹80=4⋅v2⋅r2
Step 4: Relate tension to centripetal force
The tension in the cord when the radius is r2 is given as T2=200N. This tension provides the necessary centripetal force:
T2=m⋅v22r2
Substituting the values:
200=4⋅v22r2
From this, we can express r2:
r2=4⋅v22200=v2250
Step 5: Substitute r2 into the angular momentum equation
Now substitute r2 back into the angular momentum equation:
80=4⋅v2⋅(v2250)
This simplifies to:
80=4⋅v3250
Multiplying both sides by 50:
4000=4⋅v32
Dividing both sides by 4:
1000=v32
Step 6: Solve for v2
Taking the cube root of both sides:
v2=10m/s
Final Answer
The velocity of the block at the time of breaking of the string is 10m/s.
---
The angular momentum of the block must remain constant since there are no external torques acting on it. The initial angular momentum L1 is given by:
L1=m⋅v1⋅r1
where:
- m=4kg (mass of the block)
- v1=4m/s (initial tangential velocity)
- r1=5m (initial radius)
Substituting the values into the equation:
L1=4kg⋅4m/s⋅5m=80kg m2/s
When the radius is shortened to r2 and the velocity becomes v2, the final angular momentum L2 is:
L2=m⋅v2⋅r2
Since angular momentum is conserved, we have:
L1=L2⟹80=4⋅v2⋅r2
The tension in the cord when the radius is r2 is given as T2=200N. This tension provides the necessary centripetal force:
T2=m⋅v22r2
Substituting the values:
200=4⋅v22r2
From this, we can express r2:
r2=4⋅v22200=v2250
Now substitute r2 back into the angular momentum equation:
80=4⋅v2⋅(v2250)
This simplifies to:
80=4⋅v3250
Multiplying both sides by 50:
4000=4⋅v32
Dividing both sides by 4:
1000=v32
Taking the cube root of both sides:
v2=10m/s
The velocity of the block at the time of breaking of the string is 10m/s.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A small block of mass 4kg is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius 0.5m about the hole with a tangential velocity of 4m/s. The cord is then pulled slowly from below, shorteing the radius of the circle in which the block revolves. The breaking strength of the cord is 600N. What will be radius of the circle when the cord breaks?

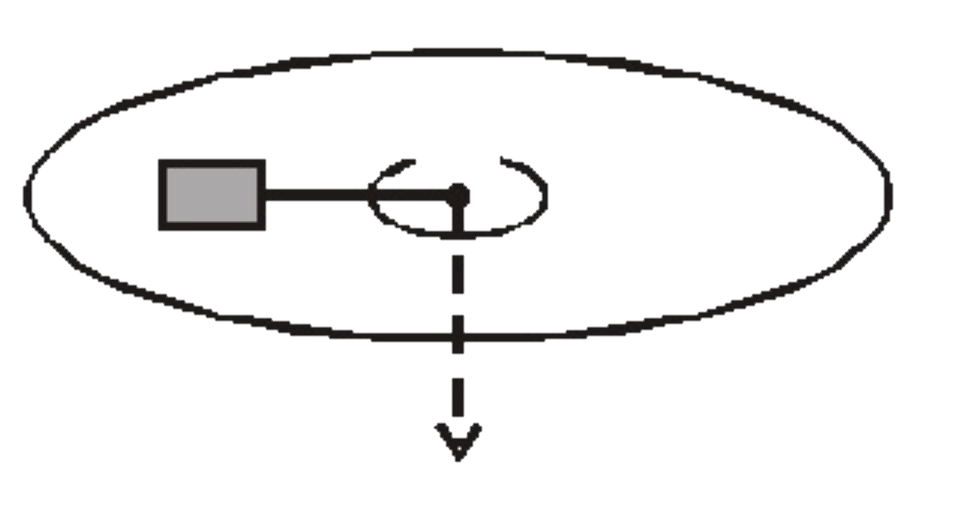
View SolutionA block of mass 0.1 kg is attached to a cord passing through a hole in a horizontal frictionless horizontal surface as shown in the figure. The block is originally revolving at a distance of 0.4 m from the hole, with an angular velocity of 2 rad s−1. The cord is then pulled from below, shortening the radius of the circle in which the block revolves to 0.2 m. Considering the block to be point mass, calculate the new angular velocity (in rad s−1)
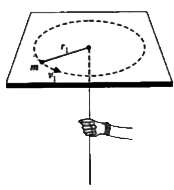
View SolutionA mass m is attached to a string passing through a small hole in a frictionless, horizontal surface. The mass is initially orbiting with a velocity v1 in a circle of radius r1 The string is then slowly pulled from below, decreasing the radius of the circles to r2 (i) What is the speed of the mass when the radius is r2 ? (ii) What is the tension in the string ? (iii) What is the work done in moving the mass m from r1 to r2?
View SolutionFigure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius r0 with a speed v0 and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m . Force F is applied at one end of rope. The force which the rope exerts on the block is:
View SolutionA block of mass m is pulled by a constant powert P placed on a rough horizontal plane. The friction coefficient the block and surface is μ. The maximum velocity of the block is.
View SolutionA block of mass m is attached to a pulley disc of equal mass, radius r by means of a slack string as shown. The pulley is hinged about its centre on a horizontal table and the block is projected with an initial velocity of 5m/s. Find the velocity when the string becomes taut.
 .
.
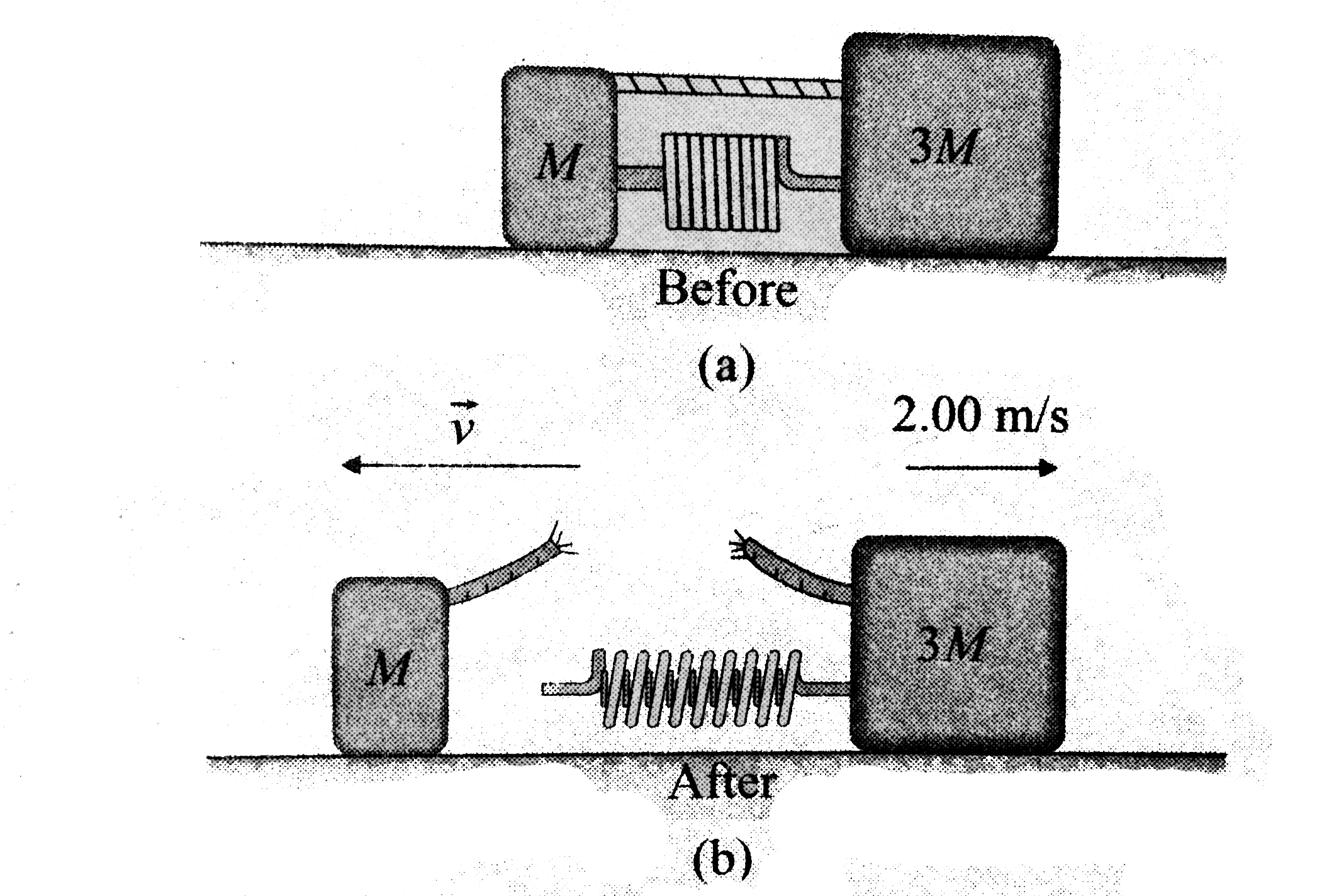
View SolutionTwo blocks of masses M and 3M are placed on a horizontal, frictionless surface. A light spring is attached to one of them and the blocks are pushed together with the spring between them. A cord initially holding the blocks together is burned, after that, the block of mass 3M moves to the right with a speed of 2.00m/s. (a) What is the velocity of the block of mass M. (b) Find the system's original elastic potential energy, taking M=0.350kg. (c) Is the original energy in the spring or in the cord? Explain your answer. (d) Is momentum of the system conserved in the bursting apart process? How can it be with large forces acting? How can it be with no motion beforehand and plenty of motion afterward?
View SolutionA block of mass m is attached with a massless in string. Breaking strength of string is 4mg. Block is moving up. The maximum acceleration and maximum retardation of the block can be

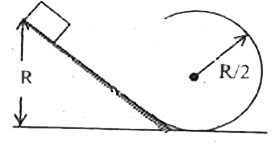
View SolutionA block of mass m is released from a height R on the frictionless incline as shown. The incline leads to a circle of radius R/2. The maximum height attained by the block is
View Solution
