A solid cube of wood of side 2a and mass M is resting on a horizontal surface. The cube is constrained to rotate about an axis passing through D and perpendicular to face ABCD. A bullet of mass m and speed v is shot at a height of 4a/3 as shown in the figure. The bullet becomes embedded in the cube. Find the minimum value of v required to topple the cube. Assume m>>M.

Let ω be the angular velocity of cube just after collison about an axis passing through D. From conservation of the angular mometum about an axis passing through D.

mv(4a3)=ID.ω
Here ID=Icom+mr2
where r= perpedicular distance of axis of rotation passing through D from centre of mass (com) of the cube =√2a
or 4mva3=[M(42+4a212)+M(2a2)]ω
or 4mva3=83Ma2.ω
ω=12mvMa........i
The cube will topple if its COM is just able to reach in a vertical height h2 as shown in figure.

Hence applying conservation of mechanical energy
12IDω2=Mg(h2−h1) (∵ID=83Ma2)
or 12(83Ma2).{12mvMa}2=Mg(√2−1a
or 12(mM)2v2=ag(√2−1)
or v=Mm[3ag(√2−1)]12
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Solved Examples
Explore 12 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.1
Explore 11 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A bullet of mass m strikes a block of mass M. The bullet remains embedded in the block. Find the amplitude of the resulting SHM.

View SolutionIn the figure shown ABCD is a lamina of mass 12kg. The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is
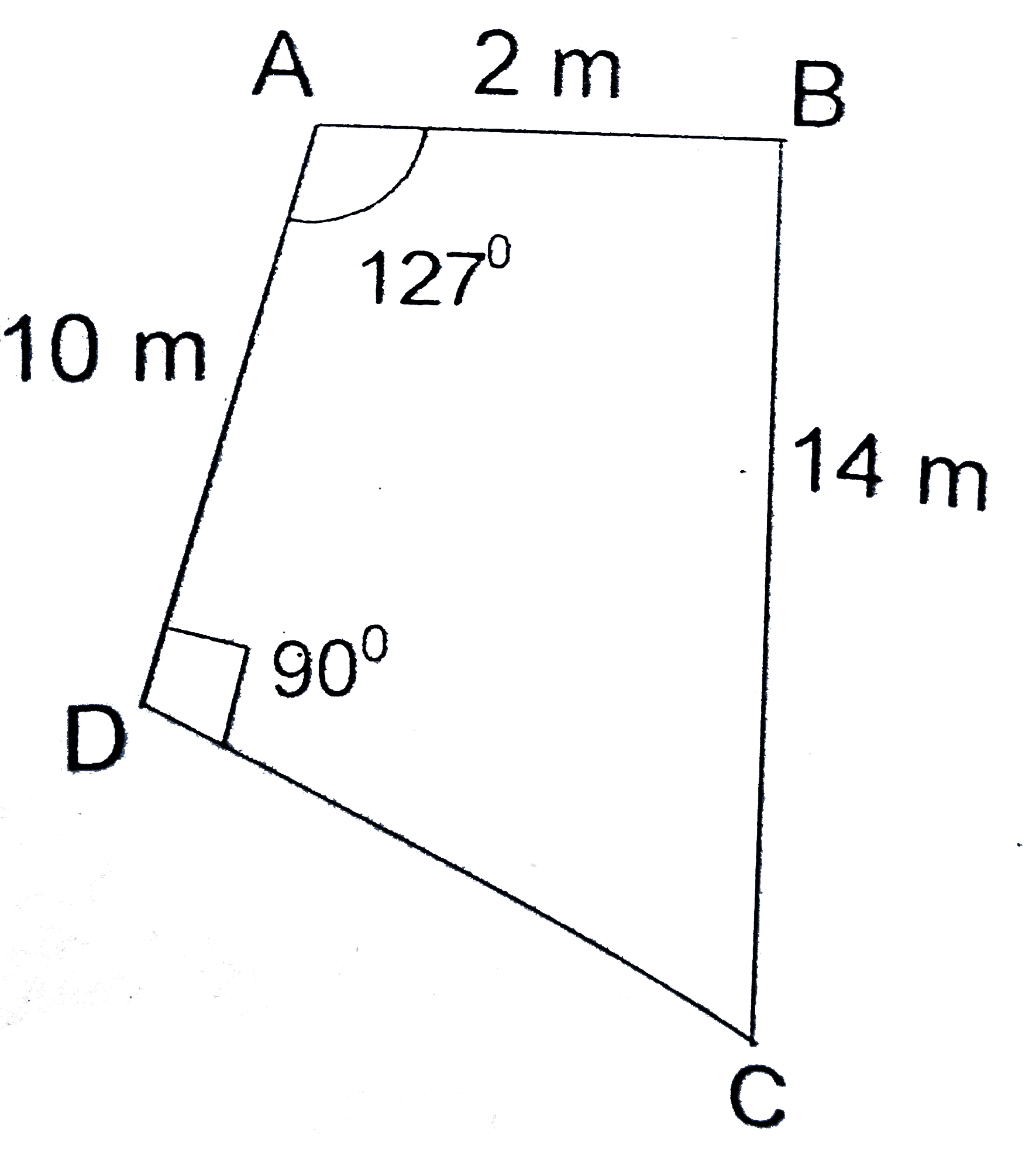
View SolutionFrom a solid sphere of M and radius R a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendiular to one of its faces is:
View SolutionFigure shows a cubical wooden block of side length a and mass M which is resting over a horizontal surface and constrained to rotate about its right lower edge D. A bullet of mass m moving horizontally, directly towards its centre with velocity v strikes and gets embedded in it. During subsequent motion the block just topples, calculate v. Assume m<<M.
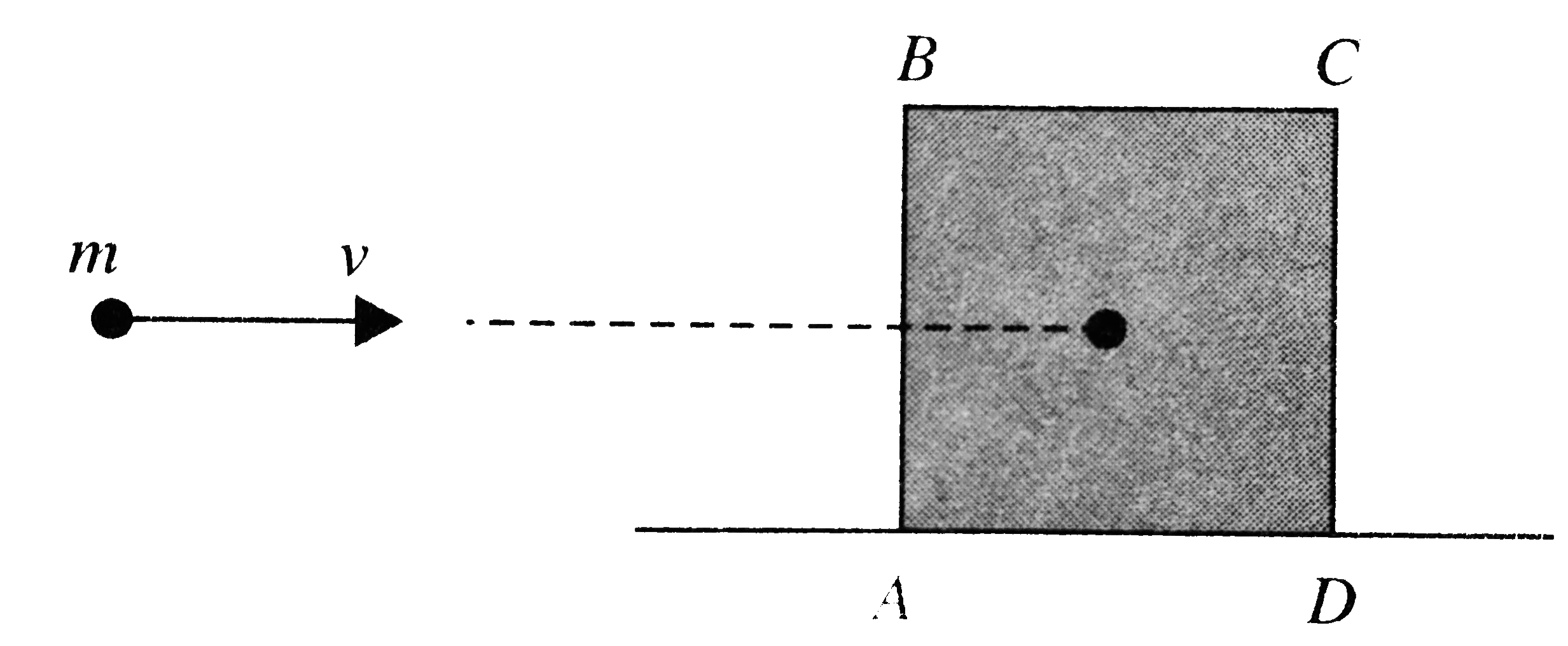
View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionA disc of mass m and radius R is kept on a smooth horizontal surface with its plane parallel to the surface. A particle of same mass m travelling with speed v0 collides with the stationery disc and gets embedded into it as shown in the figure. Then

View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
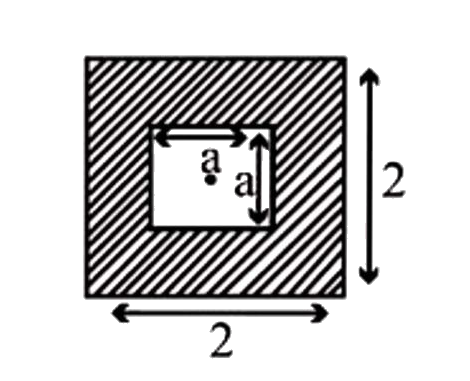
View SolutionA cube of mass m and side a is moving along a plane with constant speed vo as shown in figure. The magnitude of angular momentum of the cube about z -axis would be.
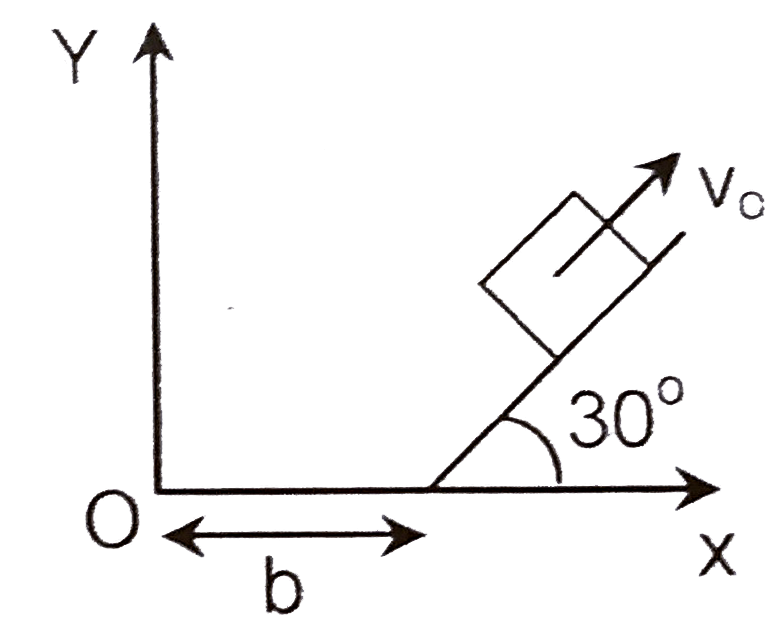
View SolutionA block of mass m is placed at the top of a smooth wedge ABC. The wedge is rotated about an axis passing through C as shown in the figure - 3.81. The minimum value of angular speed ω such that the block does not slip on the wedge is :
View Solution
A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.
View Solution