A rod of mass m is kept on a cylinder and sphere each of radius R. The masses of the sphere and cylinder are m1 and m2 respectively. If the speed of the rod is V, find the KE of the system (rod+cylider+sphere). Assume that the surfaces do not slide relative to each other.

Kinetic energy is case of rolling KE=(1+k2R2)mv22
where k=radius of gyration. For cylinder k2=12
Kcylinder=(1+12)m1v'22=34m1v'2
For rolling Kcylinder=34m1v'2

and Ksphere=12(1+25)m'2v=710m2v'2,then
Krod=Kcylinder+Ksphere=12mv2+34m1v'2+710m2v'2
where v'=v2 and m1=m2=m=6980mv2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Knowledge Check
Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
A25MR2B65MR2C45MR2D75MR2Two spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
A−GMrB−2GMrC−GM2rD−4GMr
Two plates 1 and 2 move with velocities −v and 2v respectively. If the sphere does not slide relative to the plates, assuming the masses of each body as m, find the kinetic energy of the system (plates+sphere).

View SolutionA rod of length 2 m is kept vertical inside a smooth spherical shell of radius 2m. The rod starts slipping inside the shell . Mass of the rod is 4 kg.
Angular speed of the rod(in rad/s) in the position when it becomes horizontal is

View SolutionFind the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
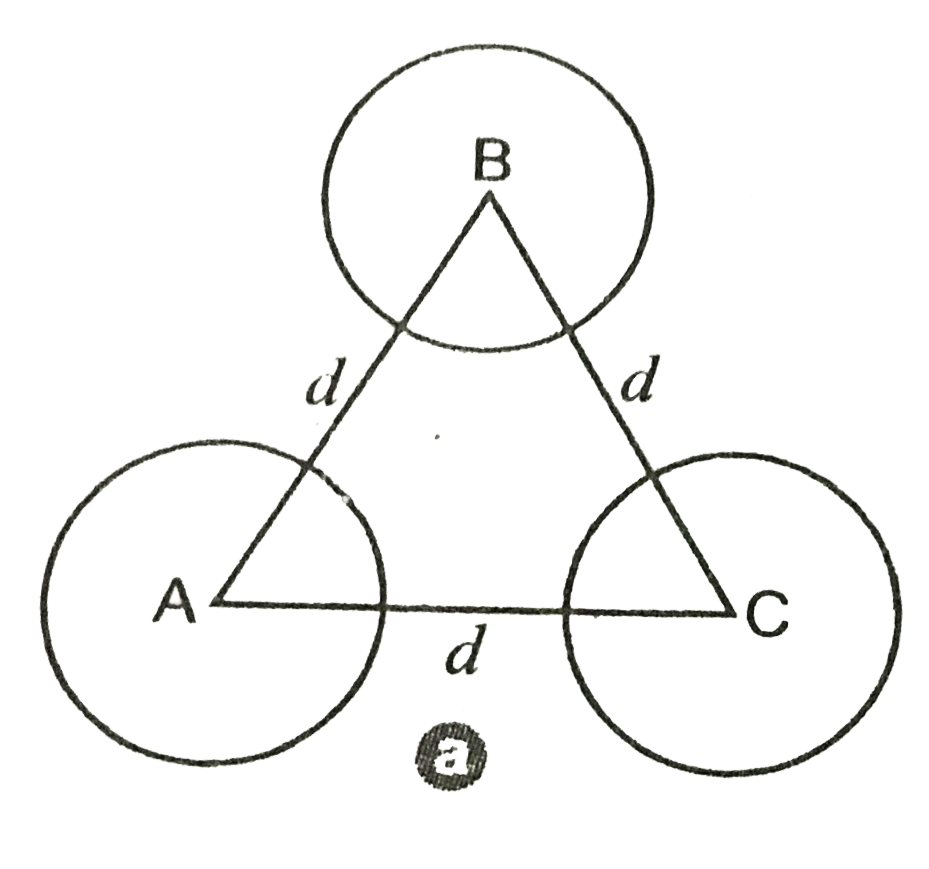
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
View SolutionTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
View SolutionA small sphere of radius R is held against the inner surface of a larger sphere of radius 6R. The mass of large and small spheres are 4M and M respectively. This arrangement is placed on a horizontal table. There is no friction between any surface of contact. The small sphere is now released. The x coordinate of the centre of the larger sphere when the smaller sphere reaches the other extreme position, is found to be (L+nR) , find n.
View Solution
