A uniform sphere of mass m and radius r rolls without sliding over a horizontal plane, rotating ahout a horizontal axle OA. In the process, the centre of the sphere moves with a veocity v along a circle of radius R. Find the kinetic energy of the sphere.
To find the kinetic energy of a uniform sphere of mass m and radius r that rolls without sliding over a horizontal plane while rotating about a horizontal axle OA, we can break down the problem into several steps.
1. Understanding the Motion:
The sphere rolls without slipping, which means that the velocity of the center of mass and the angular velocity are related. The center of the sphere moves with a velocity v along a circular path of radius R.
2. Relating Angular Velocity and Linear Velocity:
For rolling without slipping, the angular velocity ω of the sphere is related to the linear velocity v by the equation:
\(
v = r \cdot \omega
\)
Rearranging gives:
\(
\omega = \frac{v}{r}
\)
3. Calculating the Moment of Inertia:
The moment of inertia I of a uniform sphere about its center of mass is given by:
\(
I_{cm} = \frac{2}{5} m r^2
\)
When the sphere rolls about an axis that is parallel to the axis through its center of mass, we can use the parallel axis theorem:
\(
I = I_{cm} + m d^2
\)
Here, d is the distance from the center of mass to the new axis of rotation, which is R (the radius of the circular path). Thus:
\(
I = \frac{2}{5} m r^2 + m R^2
\)
4. Calculating Kinetic Energy:
The total kinetic energy K of the sphere consists of two parts: translational kinetic energy and rotational kinetic energy.
- The translational kinetic energy Kt is given by:
\(
K_t = \frac{1}{2} m v^2
\)
- The rotational kinetic energy Kr about the axis OA is given by:
\(
K_r = \frac{1}{2} I \omega^2
\)
Substituting I and ω:
\(
K_r = \frac{1}{2} \left( \frac{2}{5} m r^2 + m R^2 \right) \left( \frac{v}{r} \right)^2
\)
Simplifying this gives:
\(
K_r = \frac{1}{2} \left( \frac{2}{5} m r^2 + m R^2 \right) \frac{v^2}{r^2}
\)
5. Total Kinetic Energy:
The total kinetic energy K is the sum of translational and rotational kinetic energies:
\(
K = K_t + K_r
\)
Substituting the expressions we derived:
\(
K = \frac{1}{2} m v^2 + \frac{1}{2} \left( \frac{2}{5} m r^2 + m R^2 \right) \frac{v^2}{r^2}
\)
Combining these terms yields the final expression for the kinetic energy of the sphere.
Final Expression:
After simplification, the total kinetic energy can be expressed as:
\(
K = \frac{7}{10} m v^2 + \frac{1}{2} m R^2 \frac{v^2}{r^2}
\)
The sphere rolls without slipping, which means that the velocity of the center of mass and the angular velocity are related. The center of the sphere moves with a velocity v along a circular path of radius R.
For rolling without slipping, the angular velocity ω of the sphere is related to the linear velocity v by the equation:
\(
v = r \cdot \omega
\)
Rearranging gives:
\(
\omega = \frac{v}{r}
\)
The moment of inertia I of a uniform sphere about its center of mass is given by:
\(
I_{cm} = \frac{2}{5} m r^2
\)
When the sphere rolls about an axis that is parallel to the axis through its center of mass, we can use the parallel axis theorem:
\(
I = I_{cm} + m d^2
\)
Here, d is the distance from the center of mass to the new axis of rotation, which is R (the radius of the circular path). Thus:
\(
I = \frac{2}{5} m r^2 + m R^2
\)
The total kinetic energy K of the sphere consists of two parts: translational kinetic energy and rotational kinetic energy.
- The translational kinetic energy Kt is given by:
\(
K_t = \frac{1}{2} m v^2
\)
- The rotational kinetic energy Kr about the axis OA is given by:
\(
K_r = \frac{1}{2} I \omega^2
\)
Substituting I and ω:
\(
K_r = \frac{1}{2} \left( \frac{2}{5} m r^2 + m R^2 \right) \left( \frac{v}{r} \right)^2
\)
Simplifying this gives:
\(
K_r = \frac{1}{2} \left( \frac{2}{5} m r^2 + m R^2 \right) \frac{v^2}{r^2}
\)
The total kinetic energy K is the sum of translational and rotational kinetic energies:
\(
K = K_t + K_r
\)
Substituting the expressions we derived:
\(
K = \frac{1}{2} m v^2 + \frac{1}{2} \left( \frac{2}{5} m r^2 + m R^2 \right) \frac{v^2}{r^2}
\)
Combining these terms yields the final expression for the kinetic energy of the sphere.
After simplification, the total kinetic energy can be expressed as:
\(
K = \frac{7}{10} m v^2 + \frac{1}{2} m R^2 \frac{v^2}{r^2}
\)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A solid sphere of mass m rolls down an inclined plane a height h. Find rotational kinetic energy of the sphere.
View SolutionA uniform sphere of mass m and radius R rolls without slipping down an inclined plane set at an angle θ to the horizontal. Find
(a) the friction coefficient at which slipping is absent,
(b) the kinetic energy of the sphere t seconds after the beginning of motion.
View SolutionIf a solid sphere of mass 1 kg and radius 0.1 m rolls without slipping at a uniform velocity of 1 m/s along a straight line on a horizontal floor, the kinetic energy is
View SolutionA sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then
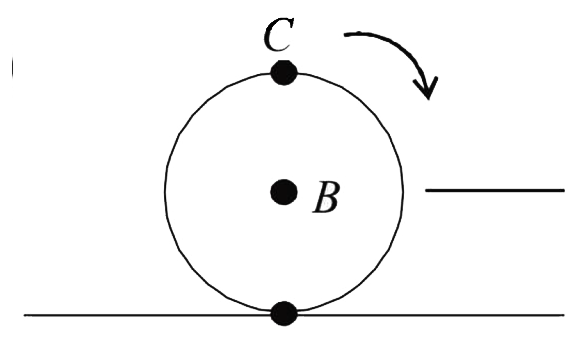
View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View Solution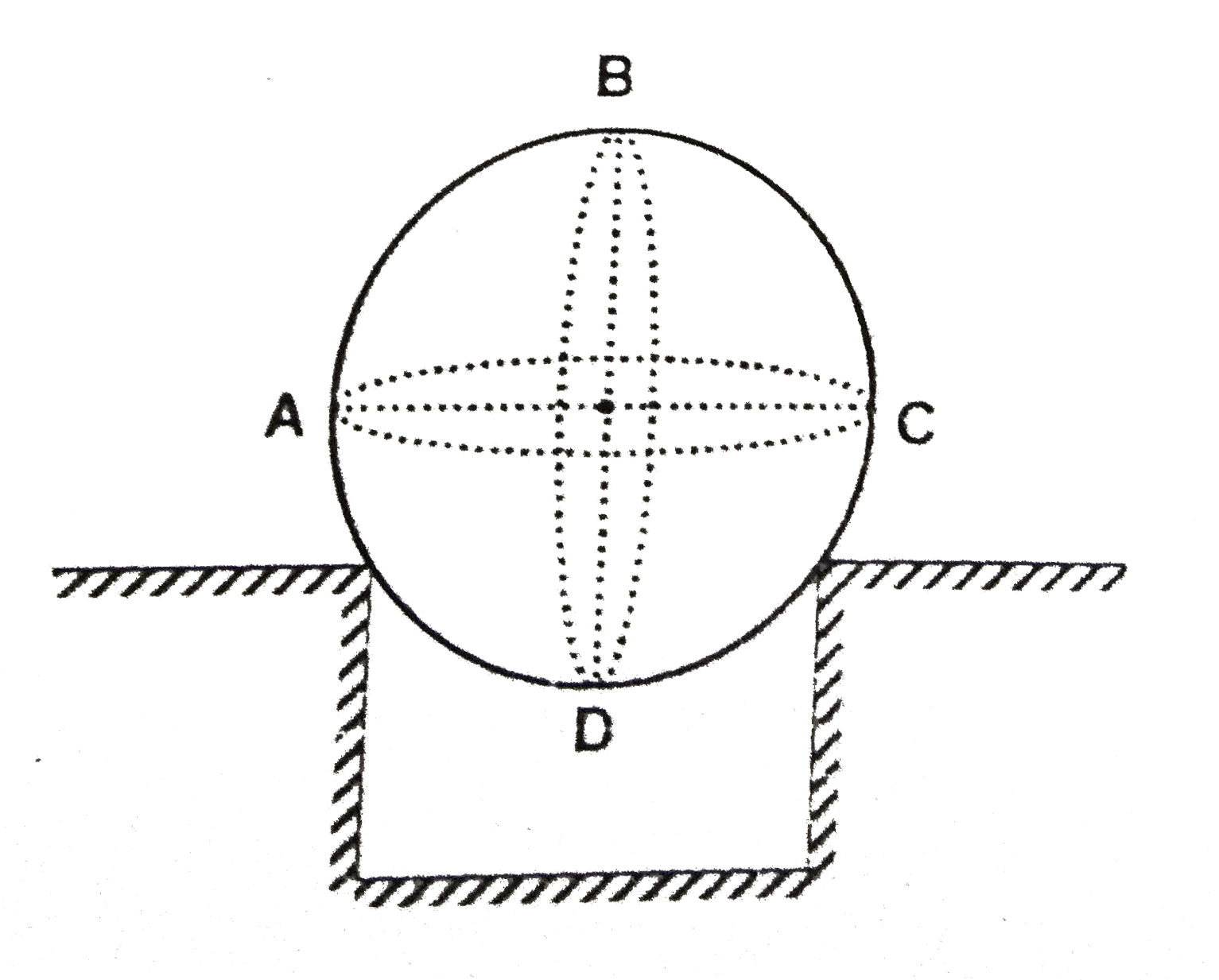
A sphere of mass m and radius r rolls without slipping over a tunnel of width d=8r5 as shown in the figure. (in the figure the sphere rolls perpendicular to the plane of the page) the velocity of centre of mass of sphere is v directed into the plane of the page. the maximum speed of a point on the sphere is
View SolutionA uniform thin spherical shell of mass m and radius R rolls down without slipping over an inclined plane of angle θ with the horizontal. The ratio of rotational kinetic energy to the total kinetic energy of the shell will be
View SolutionA solid sphere of mass m= 500gm is rolling without slipping on a horizontal surface. Find kinetic energy of a sphere if velocity of centre of mass is 5 cm/sec
View SolutionA uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
View Solution
