A boy of mass m climbs up a conveyor belt with a constant acceleration. The speed of the belt is v=√gh/6 and the coefficient of friction between the body and conveyor belt is μ=53√3. The boy starts from A and moves with the maximum possible acceleration till he reaches the highest point B.
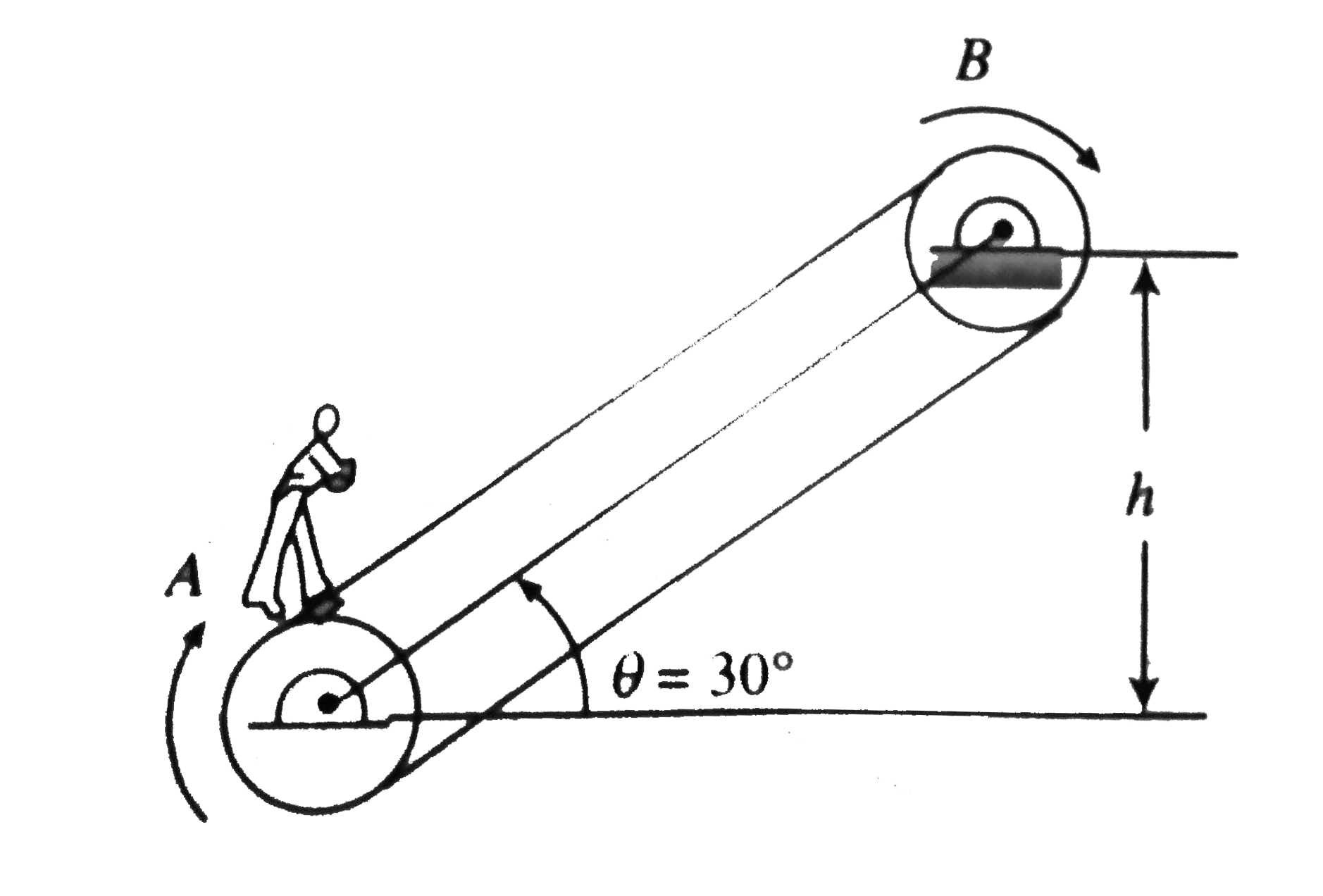
The time taken by the boy to reach the height h is
(a) √2hg
(b) √6hg
(c) 2√hg
(d) None of above
The correct Answer is:B
a=Fmax−mgsinθm
=μmgcosθ−mgsinθm=g3

AB=vt+12at2
hsin30∘=√gh6t+12g3t2
gt2+√6ght−12h=0
Solving, we get t=√6hg
vf=vi+at=√gh6+g3√6hg=3√gh6
ΔKE=12m(v2f−v2i)=23mgh
Distance moved by conveyour belt till the boy reaches B:
s=vit=√gh6√6hg=h
w.r.t. conveyor belt, distance moved by the boy,
2h−h=h
Work done by gravity w.r.t. conveyor
Wmg=−mghsin30∘=−mgh2
From the frame of belt: v1=0, vf=at=2√gh6
Wboy=ΔKE+ΔPE
=12m(v2f−v2i)+mgh2
=12m[4gh6]+mgh2=5mgh6
From the frame of ground:
Wboy+Wf+Wmg=ΔKE
Wf=23mgh+mgh−56mgh=56mgh
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Integer
14 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (sinble Correct )
19 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A boy of mass m climbs up a conveyor belt with a constant acceleration. The speed of the belt is v=√gh/6 and the coefficient of friction between the body and conveyor belt is μ=53√3. The boy starts from A and moves with the maximum possible acceleration till he reaches the highest point B.
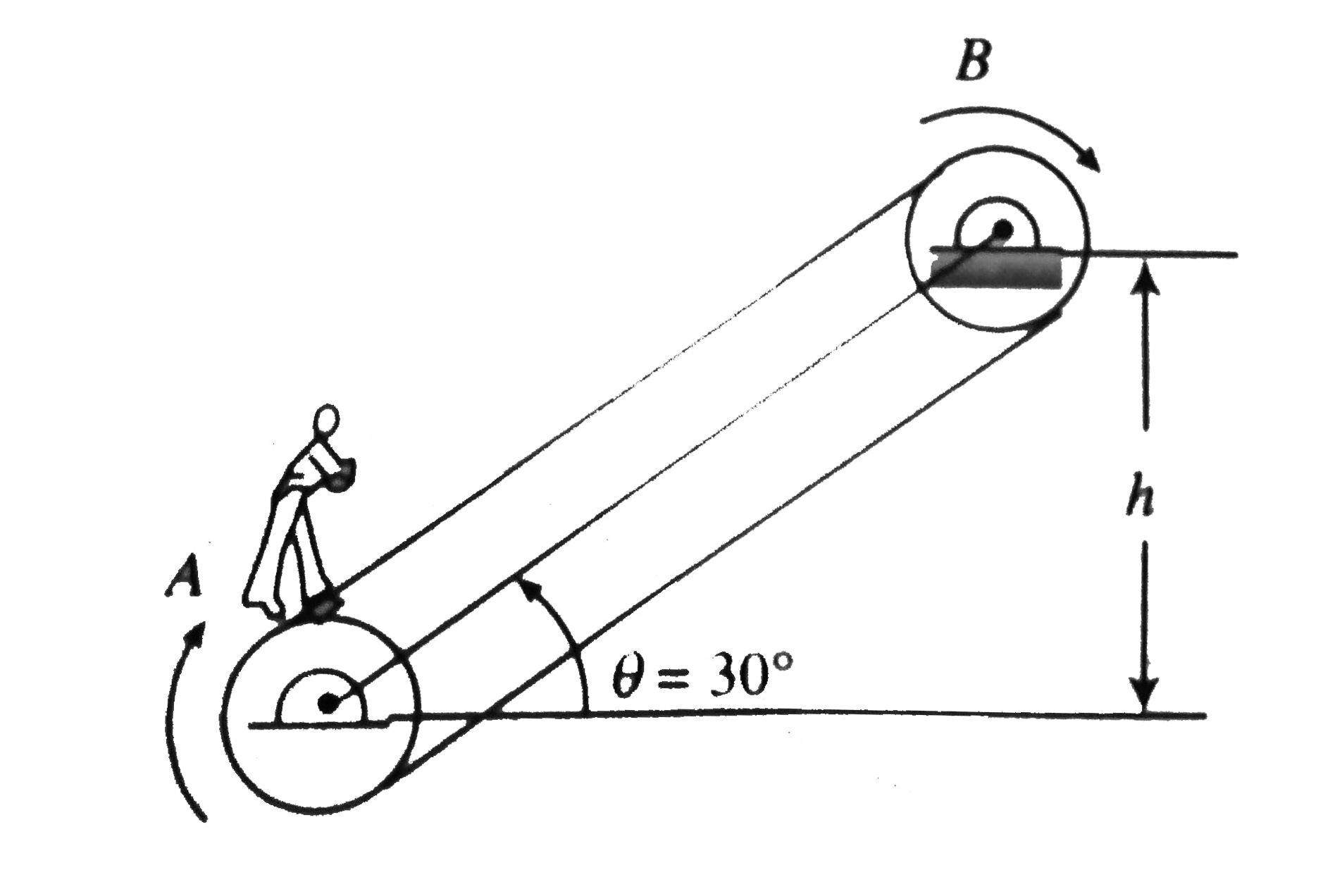
Work done by the boy is
View SolutionA boy of mass m climbs up a conveyor belt with a constant acceleration. The speed of the belt is v=√gh/6 and the coefficient of friction between the body and conveyor belt is μ=53√3. The boy starts from A and moves with the maximum possible acceleration till he reaches the highest point B.
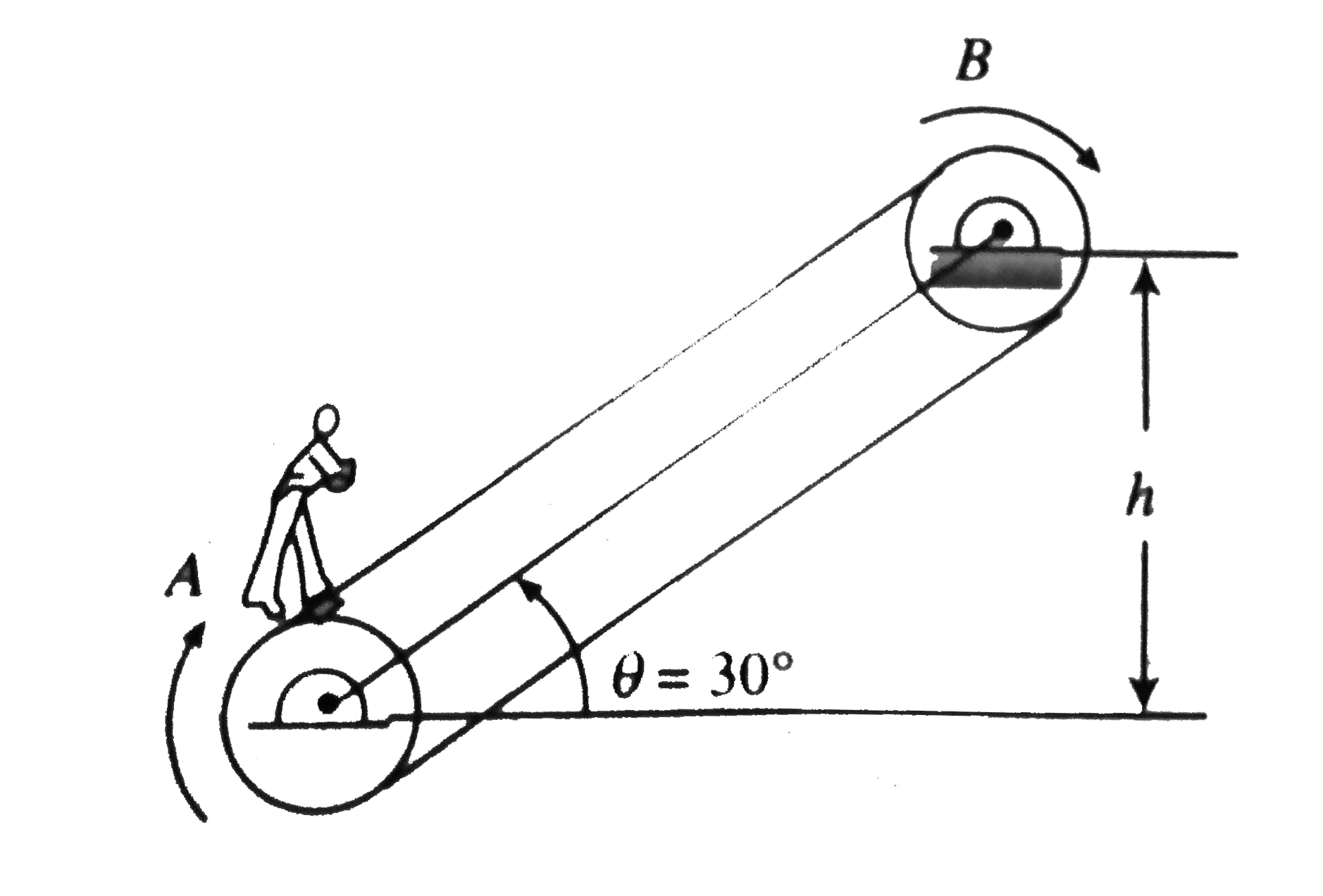
Work done by gravity to w.r.t. the conveyor belt is
View SolutionA conveyor belt is moving at a constant speed of 2m/s . A box is gently dropped on it. The coefficient of friction between them is μ=0.5 . The distance that the box will move relative to belt before coming to rest on it taking g=10ms−2 is:
View SolutionA rectangular wire frame ABCD is in vertical plane is moving with a constant acceleration a into the plane as shown . Direction of gravity is shown inn figure . A collar can move on wire AC of length l . Coefficient of friction between wire and collar is μ. Find
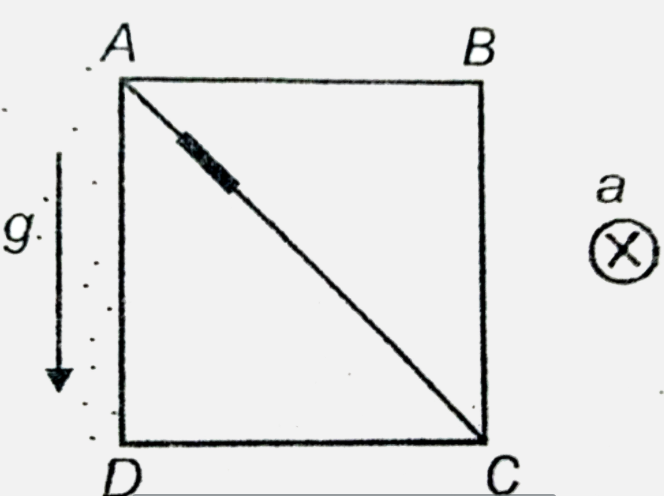 ltbr>
(i) The .....
(i) maximum acceleration a so that collar does not slip on wire.
ltbr>
(i) The .....
(i) maximum acceleration a so that collar does not slip on wire.
(ii) The time taken by collar to reach C if acceleration is half the value calculated in part
View SolutionA package rest on a conveyor belt which is initially at rest . The belt is started and moves to the right for 1.3s with a constant acceleration of 2m/s2. The belt then moves with a constant deceleration a2 and comes to a stop after a total displacement of 2.2m . Knowing that the coefficient of friction between the package and the belt are μs=0.35 and μk=0.25 , determine (a) the deceleration a2 of the belt , (b) the displacement of the package relative to the belt as the belt comes to a stop. (g=9.8m/s2)

View SolutionA uniform cylinder of mass M and radius R is placed on a rough horizontal board, which in turn is placed on a smooth surface. The coefficient of friction between the board and the cylinder is μ. If the board starts accelerating with constant acceleration a, as shown in the figure, then

Option1
for pure rolling motion of the cylinder, direction of frictional force is forward and its magnitude is M a / 3
Option2
the maximum value of a, so that cyliner performs pure rolling is 3 μ g
Option3
The acceleration of the centre of mass of te cylinder under pure rolling condition for the given a is a / 3
Option4
none of these
View SolutionA block of mass 2 kg rests on an inclined plane which makes an angle of 30∘ with the horizontal. The coefficient of friction between the block and the surface is √3/2. (i) What force should be applied on the block so that it moves down without any acceleration ? (ii) What force should be applied on the block so that it moves up without any acceleration ? (iii) Calculate the ratio of the powers in the above two cases if the block moves with uniform speed in both the cases.
View SolutionA body of mass 0.3kg is taken up an inclined plane of length 10m and height 5m, and then allowed to slide down to the bottom again. The coefficient of friction between the body and the plane is 0.15. What is the
(a) work done by the gravitational force over the round trip.
(b) work done by the applied force over the upward journey
(c ) work done by frictional force over the round trip.
(d) kinetic energy of the body at the end of the trip.
How is the answer (d) related to the first three answers ?
m=0.3kg, OA=10m, BA=5m
View SolutionIn the figure the wedge is pushed with an acceleration of √3m/s2. It is seen that the block start climbing up on the smooth inclined face of wedge . What will be the time taken by the block to reach the top?
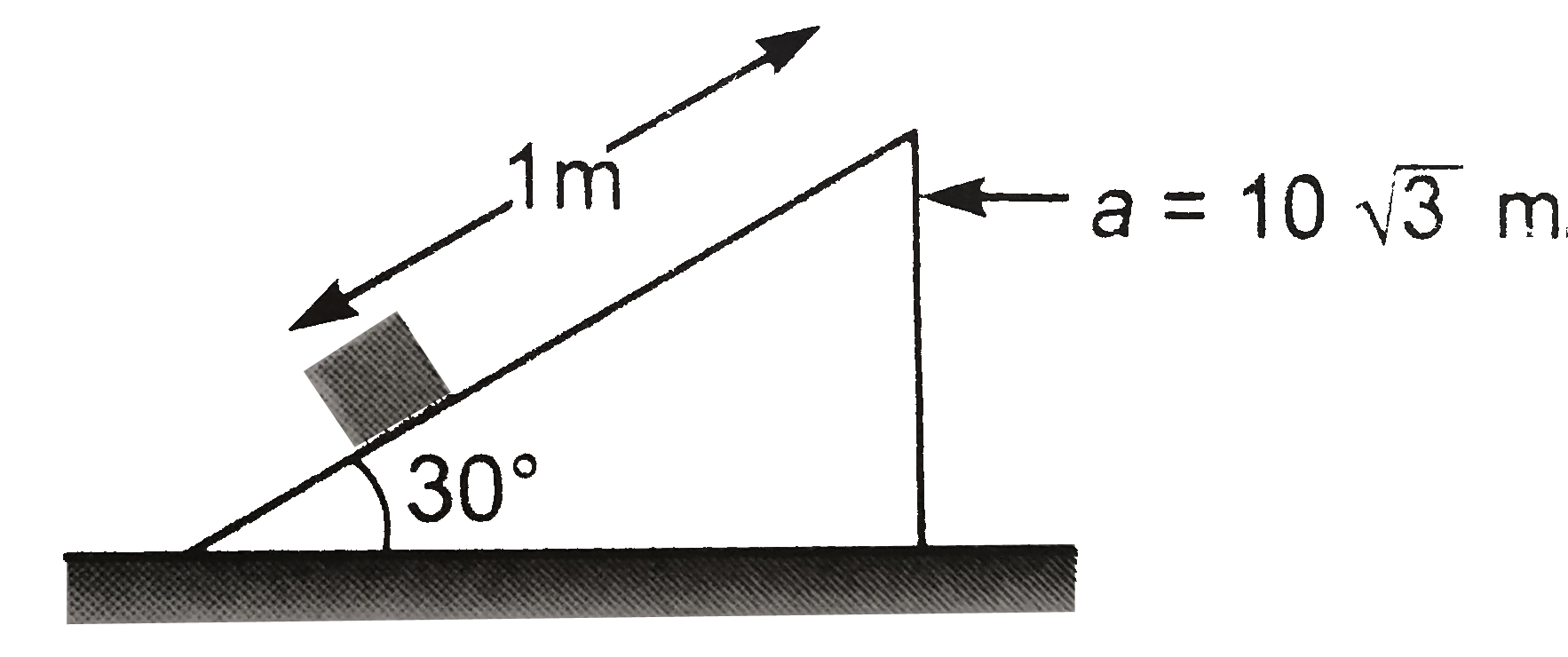
View SolutionIn the figure the wedge is pushed with an acceleration of √3m/s2. It is seen that the block start climbing up on the smooth inclined face of wedge . What will be the time taken by the block to reach the top?

View Solution
