Two blocks having masses 8kg and 16kg are connected to the two ends of a light spring. The system is placed on a smooth horizontal floor. An inextensible string also connects B with ceiling as shown in the figure at the final moment. Initially the spring has its natural length. A constant horizontal force F is applied to the heavier block as shown. What is the maximum possible value of F so the lighter block doesn't loose contact with ground?

The correct Answer is:30N
Draw FBD of B to get extension in spring. Instant when block B just loses contact with ground net force on it is zero.
kx−Tcosθ=0⇒Tsinθ+N−mg=0 to rise N=0
kxcosθsinθ=mg
x=mgktanθ=80k×(4/3)=60k
If spring has to just extend till this value at their extension it should be at rest.
Now we apply work energy theorem to get
Fx=12kx2⇒F=30N

Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Single Correct
Explore 100 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.5
Explore 15 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
Two identical blocks A and B each of mass M are connected to each other through a light string. The system is placed on a smooth horizontal floor. When a constant force F is applied horizontally on the block A, find the tension in the string.
View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is

View Solution
Knowledge Check
Two blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
A100NB200NC300ND400N
Two blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionThree blocks of masses 5 kg, 10 kg and 15 kg are connected to - light inextensible string placed on smooth horizontal tble as shown below.
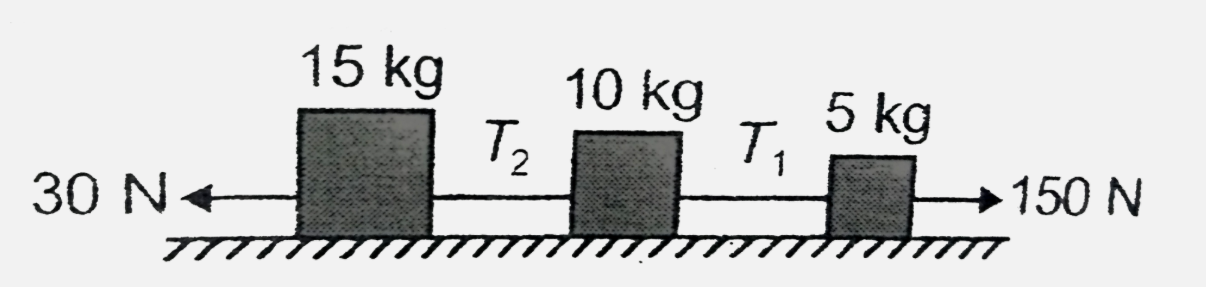
T1T2 will be
View SolutionTwo blocks of masses 7 kg and 3 kg are connected by a spring of stiffness 1000Nm−1 and placed on a smooth horizontal surface. They are acted by horizontal forces of 72 N and 32 N in opposite directions as shown in the figure. When accelerations of the blocks are equal and constant, the extension of the spring is
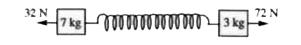
View SolutionTwo blocks of mass 8 kg and 5 kg are connected by a heavy rope of mass 3 kg. An upward force of 180 N is applied as shown in the figure. The tension in the string at point P will be:

View SolutionTwo block of mass 1kg and 2kg are connected by a string AB of mass 1kg. The blocks are placed on a smooth horizontal surface. Block of mass 1kg is pulled by a horizontal force F of magnitude 8N. Find the tension in the string at points A and B

View SolutionAssertion: Two blocks A and B are connected at the two ends of an ideal spring as shwon in figure. Initially, spring was released. Now block B is pressed. Linear momentum of the system will not remain constan till the spring reaches its initial natural length.
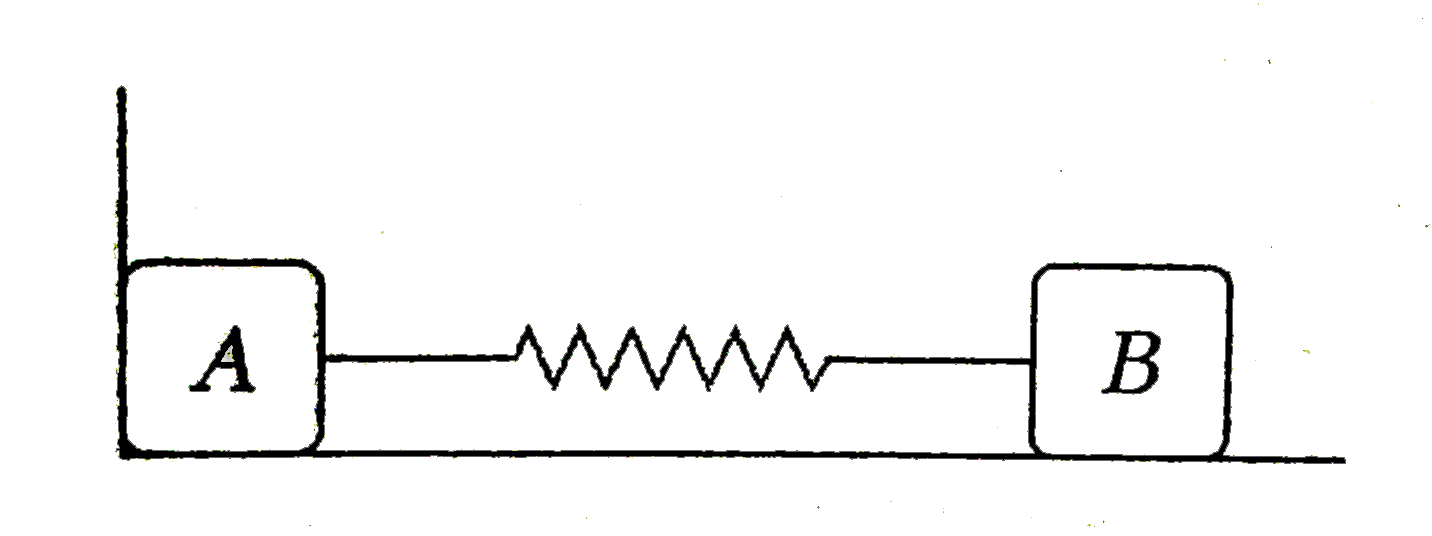
Reason: An external force will act from the wall on block A.
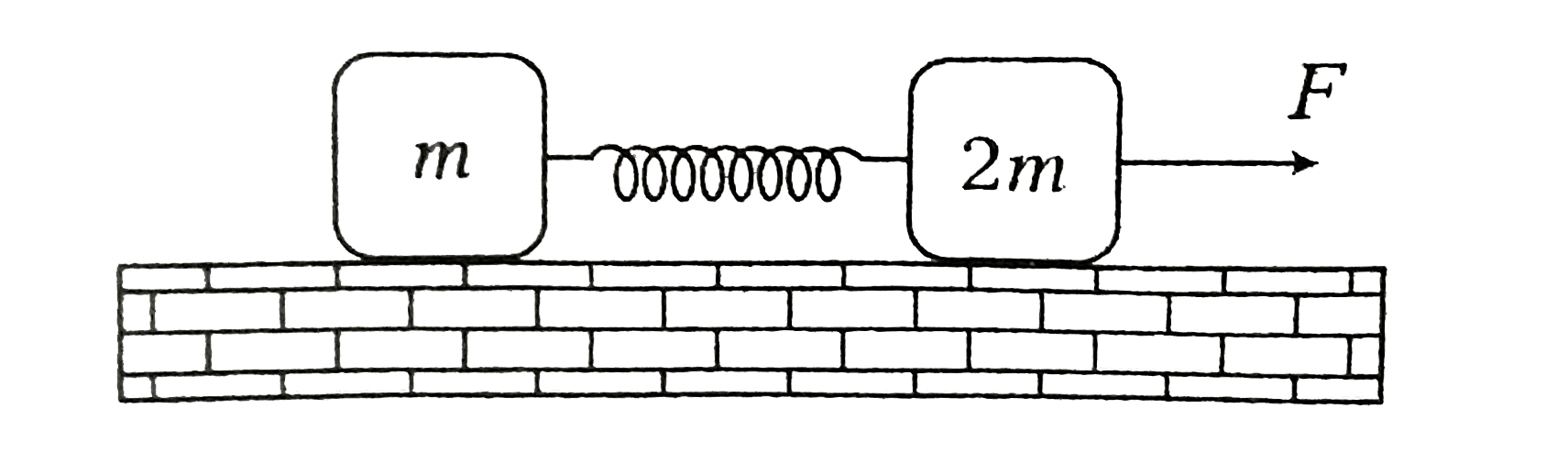
View SolutionTwo blocks of mass m and 2m are kept on a smooth horizontal surface. Theya are connected by an ideal spring of force constant k. Initially the spring is unstretched. A constant force is applied to the heavier block in the direction shown in figure. Suppose at time t displacement of smaller block is x1 then displacement of the heavier block at this moment would be
View Solution

