Statement I: A block is lying stationary as on inclined plane and coefficient of friction is μ. Friction on block is μmgcosθ.

Statement II: Contact force on block is mg.
Statement I is true, statement II is true, Statement II is the correct explanation for statement I.
Statemet I is true, Statement II is true , Statement II is NOT the correct explanation for Statement I
Statement I is True, Statement II is False.
Statement I is False, Statement II is true
The correct Answer is:D
Contact force is the sum of friction and normal reaction.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Linked Comperhension
46 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
Knowledge Check
A block of mass m is at rest on an inclined plane. The coefficient of static friction is μ. The maximum angle of incline before the block begins to slide down is :
Atan−1(μ/m)Btan−1(μ)Ctan−1(μ/2)Dcos−1(μ)A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μ
A block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
View SolutionA block of mass m is placed over rough inclined plane having inclination 30∘ .The co-efficient of friction between the block and inclined plane is 0.75.The contact force on the block is x4mg. Find the value of x
View SolutionA block slides down an inclined plane that makes an angle θ with the horizontal. If the coefficient of kinetic friction is μ, find the acceleration of the block.
View SolutionA block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
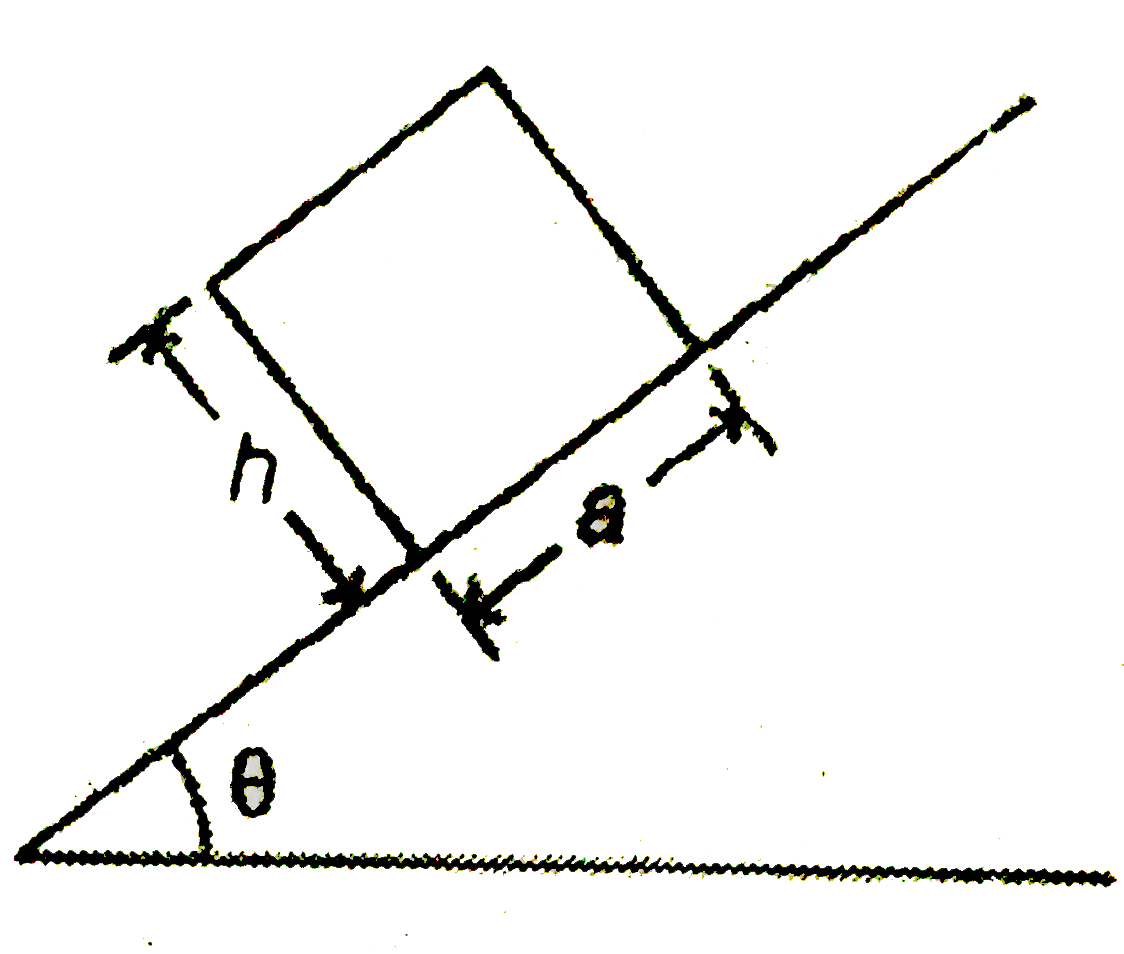
View SolutionStatement I: A block of mass m is placed on a smooth inclined plane of inclinaton θ with the horizontal. The force exerted by the plane on the block has a magnitude mgcosθ.
Statement II: Normal reaction always acts perpendicular to the contact surface.
View SolutionA small block is resting on an inclined plane (co-efficient of friction μ>tanθ) as shown in the figure. The inclined plane is given a constant horizontal acceleration 'a' towards right.
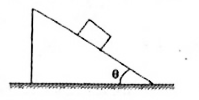
(a) Find the range of 'a' such that the bock does not slide on the plane.
(b) Find the value of 'a' such that the firction force between the block and the plane is zero.
View Solution
