When forces F1, F2, F3, are acting on a particle of mass m such that F2 and F3 are mutually perpendicular, then the particle remains stationary. If the force F1 is now removed then the acceleration of the particle is
R3m
R1+R2m
R1−R2m
R1m
The correct Answer is:A
To solve the problem step by step, we will analyze the forces acting on the particle and apply Newton's laws of motion.
Step 1: Understand the Forces Acting on the Particle
We have three forces acting on a particle of mass m:
- F1
- F2
- F3
Given that F2 and F3 are mutually perpendicular, we can visualize them as acting along the x-axis and y-axis respectively.
Step 2: Condition for the Particle to be Stationary
For the particle to remain stationary, the net force acting on it must be zero. This means:
F1+F2+F3=0
Since F2 and F3 are perpendicular, we can express the net force in terms of their magnitudes:
F1=√F22+F23
Step 3: Removing Force F1
Now, if we remove the force F1, the remaining forces acting on the particle are F2 and F3. Since F2 and F3 are still present, we need to find the resultant force acting on the particle.
Step 4: Calculate the Resultant Force
The resultant force Fnet when F1 is removed is simply the vector sum of F2 and F3:
Fnet=√F22+F23
Step 5: Apply Newton's Second Law
According to Newton's second law, the net force acting on an object is equal to the mass of the object multiplied by its acceleration:
Fnet=m⋅a
Substituting the expression for Fnet:
√F22+F23=m⋅a
Step 6: Solve for Acceleration a
To find the acceleration a, we rearrange the equation:
a=√F22+F23m
Final Answer
Thus, the acceleration of the particle after removing force F1 is:
a=√F22+F23m
---
We have three forces acting on a particle of mass m:
- F1
- F2
- F3
For the particle to remain stationary, the net force acting on it must be zero. This means:
F1+F2+F3=0
Since F2 and F3 are perpendicular, we can express the net force in terms of their magnitudes:
F1=√F22+F23
Now, if we remove the force F1, the remaining forces acting on the particle are F2 and F3. Since F2 and F3 are still present, we need to find the resultant force acting on the particle.
The resultant force Fnet when F1 is removed is simply the vector sum of F2 and F3:
Fnet=√F22+F23
According to Newton's second law, the net force acting on an object is equal to the mass of the object multiplied by its acceleration:
Fnet=m⋅a
Substituting the expression for Fnet:
√F22+F23=m⋅a
To find the acceleration a, we rearrange the equation:
a=√F22+F23m
Thus, the acceleration of the particle after removing force F1 is:
a=√F22+F23m
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Multiple Correct
Explore 11 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Assertion-reasoning
Explore 15 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Subjective
Explore 15 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
When forces F1 , F2 , F3 are acting on a particle of mass m such that F2 and F3 are mutually prependicular, then the particle remains stationary. If the force F1 is now rejmoved then the acceleration of the particle is
View SolutionF1 particle of oxysome
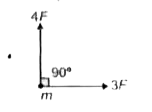
View SolutionWhen a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
View SolutionA particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionThe variation of force (F) acting on a particle of mass 800 g with position (x) is as shown in figure. The time period of oscillation of the particles is
View SolutionA particle moves under force F=5(x−2)3 .Motion of the particle is
View SolutionForces F1andF2 act on a point mass in two mutually perpendicular directions. The resultant force on the point mass will be
View SolutionForces F1andF2 act on a point mass in two mutually perpendicular directions. The resultant force on the point mass will be
View SolutionTwo forces f1=4N and f2=3N are acting on a particle along positve X−axis and negative y−axis respectively. The resultant force on the particle will be−
View Solution