A locomotive accelerates a train of identical railway carts. The carts are numbered consecutively with the cart next to locomotive having the number 1. The tension in the connection between the carts with numbers 4 and 5 is three times begger than the tension in the connection between the carts with numbers 14 and 15. What is the number of the last cart? there is no resistance to the train's motion.
To solve the problem, we need to analyze the situation involving the tensions between the railway carts and how they relate to the number of carts.
1. Understanding the Problem:
- We have a locomotive pulling a series of identical railway carts.
- The carts are numbered consecutively, starting from 1 next to the locomotive.
- The tension between carts 4 and 5 is three times the tension between carts 14 and 15.
2. Define Variables:
- Let n be the total number of carts.
- The mass of each cart is m.
- The acceleration of the train is a.
3. Calculate Tension Between Carts:
- The tension T4−5 between carts 4 and 5 can be expressed as:
T4−5=(n−4)⋅m⋅a
Here, (n−4) is the number of carts being pulled by cart 4 (from cart 5 to cart n).
- The tension T14−15 between carts 14 and 15 can be expressed as:
T14−15=(n−14)⋅m⋅a
Here, (n−14) is the number of carts being pulled by cart 14 (from cart 15 to cart n).
4. Set Up the Equation:
- According to the problem, the tension between carts 4 and 5 is three times that between carts 14 and 15:
T4−5=3⋅T14−15
- Substituting the expressions for tension, we get:
(n−4)⋅m⋅a=3⋅(n−14)⋅m⋅a
5. Simplify the Equation:
- Since m and a are common on both sides, we can cancel them out:
n−4=3(n−14)
- Expanding the right side:
n−4=3n−42
6. Rearranging the Equation:
- Bring all terms involving n to one side:
n−3n=−42+4
−2n=−38
- Dividing by -2:
n=19
7. Conclusion:
- The total number of carts is n=19. Therefore, the last cart is numbered 19.
Final Answer:
The number of the last cart is 19.
- We have a locomotive pulling a series of identical railway carts.
- The carts are numbered consecutively, starting from 1 next to the locomotive.
- The tension between carts 4 and 5 is three times the tension between carts 14 and 15.
- Let n be the total number of carts.
- The mass of each cart is m.
- The acceleration of the train is a.
- The tension T4−5 between carts 4 and 5 can be expressed as:
T4−5=(n−4)⋅m⋅a
Here, (n−4) is the number of carts being pulled by cart 4 (from cart 5 to cart n).
T14−15=(n−14)⋅m⋅a
Here, (n−14) is the number of carts being pulled by cart 14 (from cart 15 to cart n).
- According to the problem, the tension between carts 4 and 5 is three times that between carts 14 and 15:
T4−5=3⋅T14−15
- Substituting the expressions for tension, we get:
(n−4)⋅m⋅a=3⋅(n−14)⋅m⋅a
- Since m and a are common on both sides, we can cancel them out:
n−4=3(n−14)
- Expanding the right side:
n−4=3n−42
- Bring all terms involving n to one side:
n−3n=−42+4
−2n=−38
- Dividing by -2:
n=19
- The total number of carts is n=19. Therefore, the last cart is numbered 19.
The number of the last cart is 19.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.3
19 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.4
13 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
"Carts with rubber tyres are better than those with iron tyres". Why ?
View SolutionA horse has to pull a cart harder in the initial stange of his motion . Why ?
View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?

View SolutionA force F=2t2 is applied to the cart of mass 10 Kg, initially at rest. The speed of the cart at t = 5 s is -
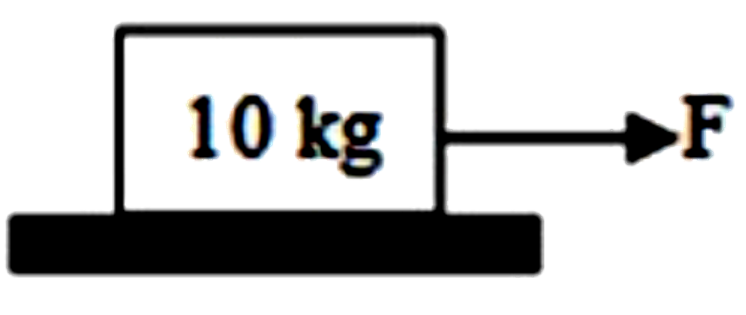
View Solution
Consider the figure shown here of a moving cart C. if the coefficient of friction between the block A and the cart is μ, then calculate the minimum acceleration a of the cart C so that the block A does not fall.
View SolutionThe minimum acceleration that must be impprted to the cart in the figure so that the block A will not fall (given μ is the coefficient if friction between the surface of block and cart) is given by:

View SolutionA cart moves with a constant speed along a horizontal circular path. From the cart, a particle is thrown up vertically with respect to the cart.
View SolutionA block of mass m is in contact with the cart C as shown in The coefficient of static friction between the block and the cart is μ The acceleration a of the cart that will prevent the block from falling satisfies
 .
.
View SolutionA body is just supported at the face of a cart moving at an acceleration. The acceleration of the cart so that the body does not slide
View SolutionA block of mass m is in contact with the cart C as shown in figure -
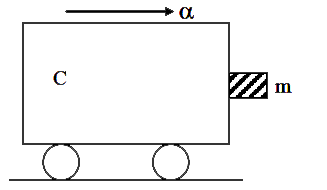
The coefficient of static friction between the block and the cart is μ , The accelertion α of the cart that will prevent the block from failing satisfies -
View Solution
