Three blocks A, B, and C of masses 3M,2M, and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is a1,a2 and a3 , respectively, then

The value of acceleration a3 at the moment spring PQ is cut is
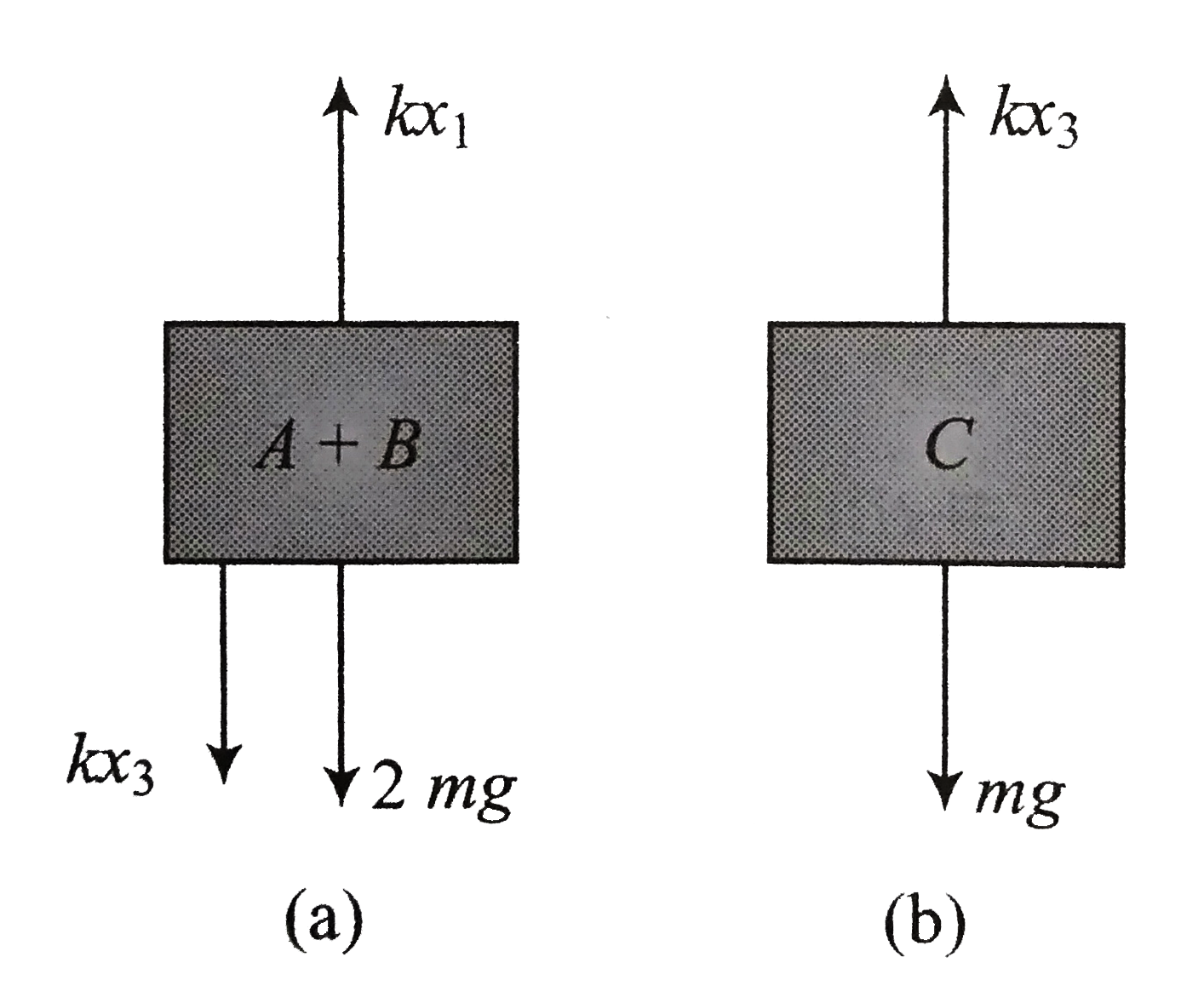
The system is in equlibrium :
kx3=mg..(i)
form fig.
2mg+kx3=kx1 …(ii)
form fig
∴3mg=kx1
(a) When the spring between ceiling and block is cut, then the elongation of spring between B and C remains same just after cutting

∴ac=0(kx3=mg)
For (A+B)
kx3+2mg=3mg
∴3mg=2ma
∴a=32g=15ms−2
∴aA=aB=15ms−2
For tension (from FBD of B),
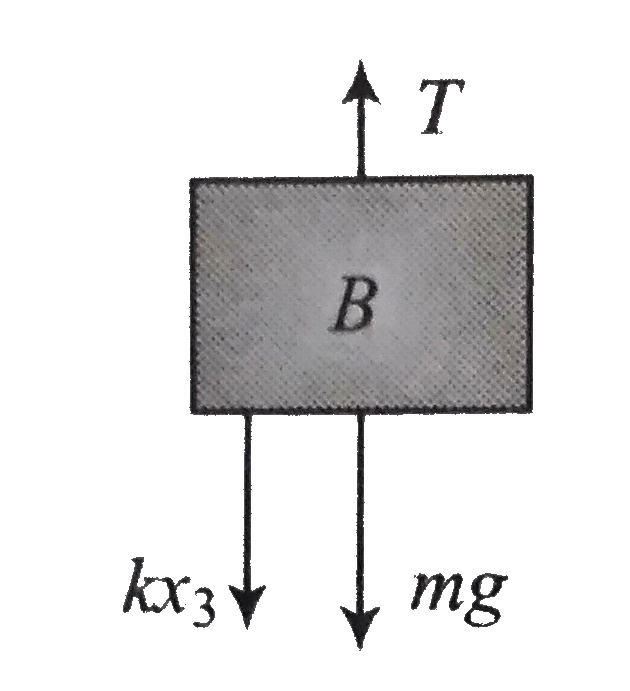
mg+kx3−T=maB
mg+mg−T=3mg2
∴T=mg2
(b) When string between A and B is cut, the elongation in spring do not change just after cutting the string.
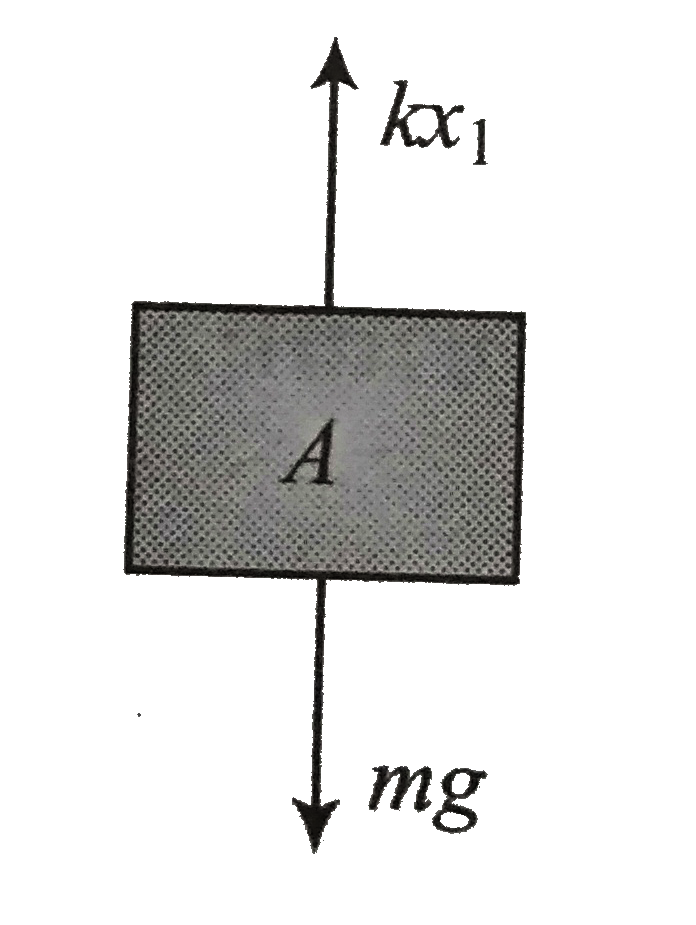
mg−kx1=maA
mg−3mg=maA {kx1=3mg}
−2mg=maA
aA=−2g
∴aA=2g (upwards)
For B
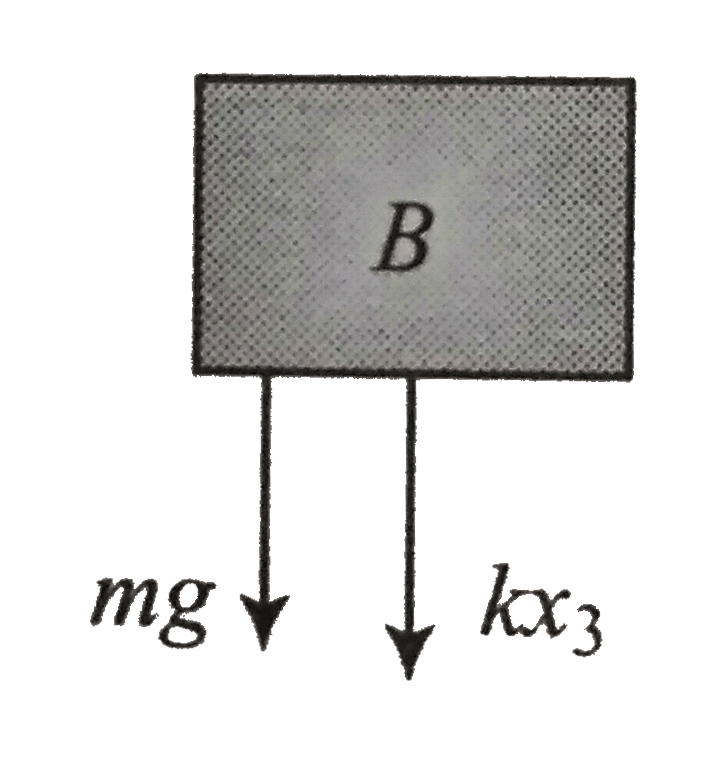
mg+kx3=maB
mg+mg=maB {∴kx3=mg}
∴aA=2g(downward)
for C, 
mg−kx3=mac
or mg−mg=mac {kx3=mg}
ac=0
T=0
(c ) when spring between B and C is cut.
for C, mg=mac
∴ac=g (downward)

The acceleration of A and B will be equal, taking A+B together as system
2mg−kx1=2maB {∴aA=aB}
2mg−3mg=2maB {∴kx1=3mg}
∴aB=−g2
∴aA=aB=g2 (upward)

For tension in string between A and B, considering the FBD of B only

T−(mg)=maB
T=mg+mg2=3mg2.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
Three blocks A, B, and C of masses 3M,2M, and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is a1,a2 and a3 , respectively, then

The value of acceleration a2 at the moment spring TU is cut is
View SolutionThree blocks A, B, and C of masses 3M,2M, and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is a1,a2 and a3 , respectively, then

The value of acceleration a1 at the moment string RS is cut is
View SolutionFind the relation between acceleration of blocks a1,a2 and a3.

View SolutionTwo blocks A and B of same mass m attached with a light spring are suspended by a string as shown in fig. Find the acceleration of block A and B just after the string is cut.
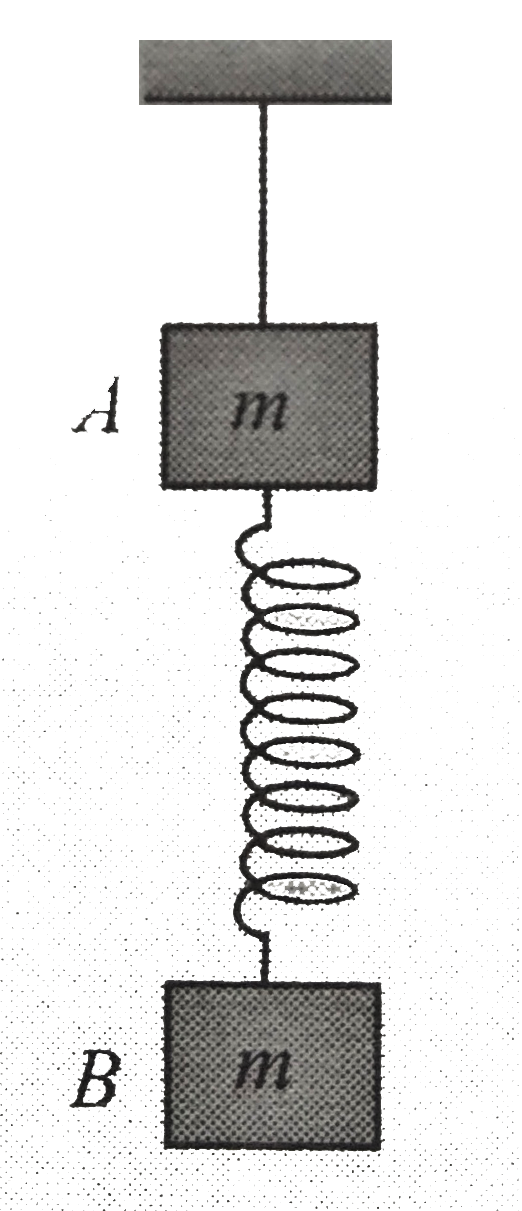
View Solution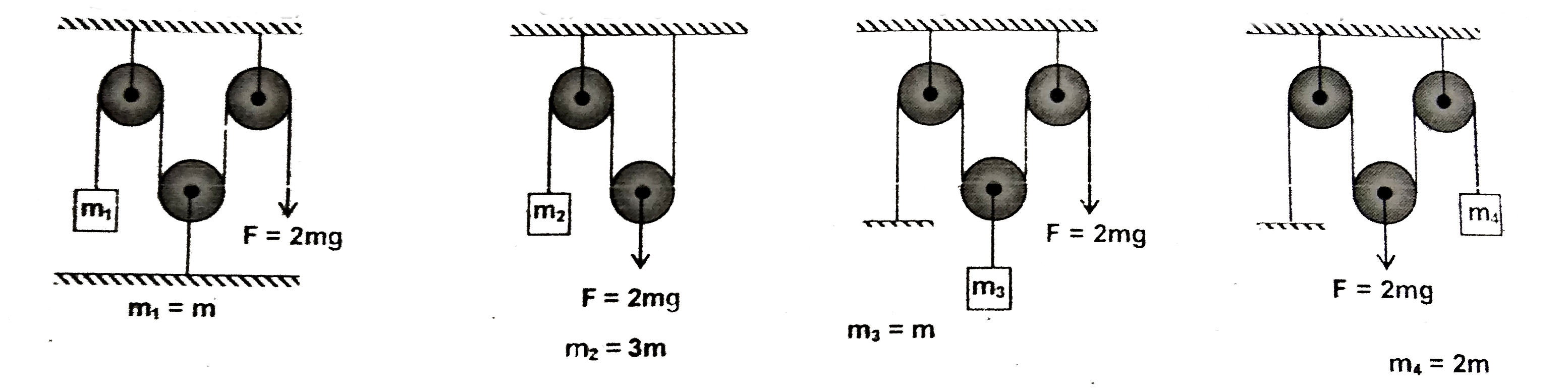
All the blocks are attached to an ideal rope which passes over an ideal pulley. If acceleration of blocks m1,m2,m3 and m4 and a1,a2,a3 and a4 respectively then choose the correct option.
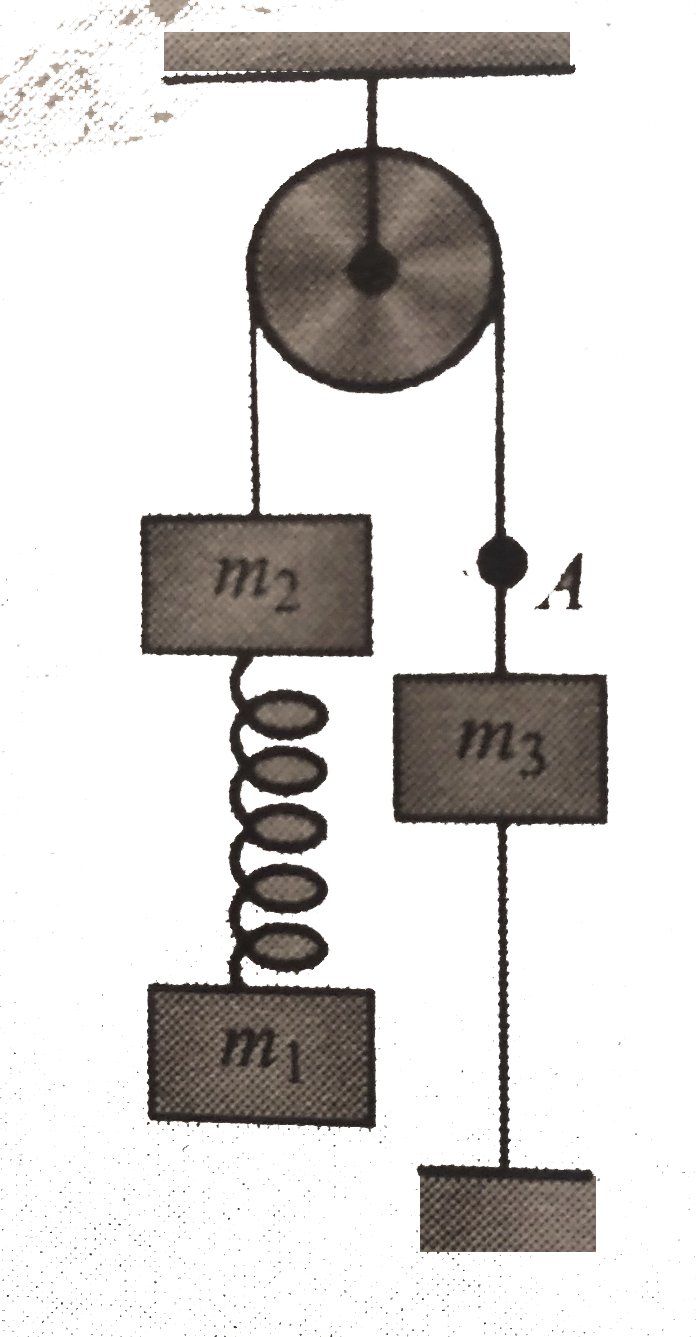
View SolutionThree blocks arranged with pullwy and spring as shown in fig. If the string connecting blocks m2 and m3 is cut at point A, find the acceleration of masses m1,m2 and m3. Just after the string is cut at point A.
View SolutionFigure shows two blocks each of mass m system is released from rest. If acceleration of blocks A and B at any instant (not initially) are a1 and a2, respectively. Then
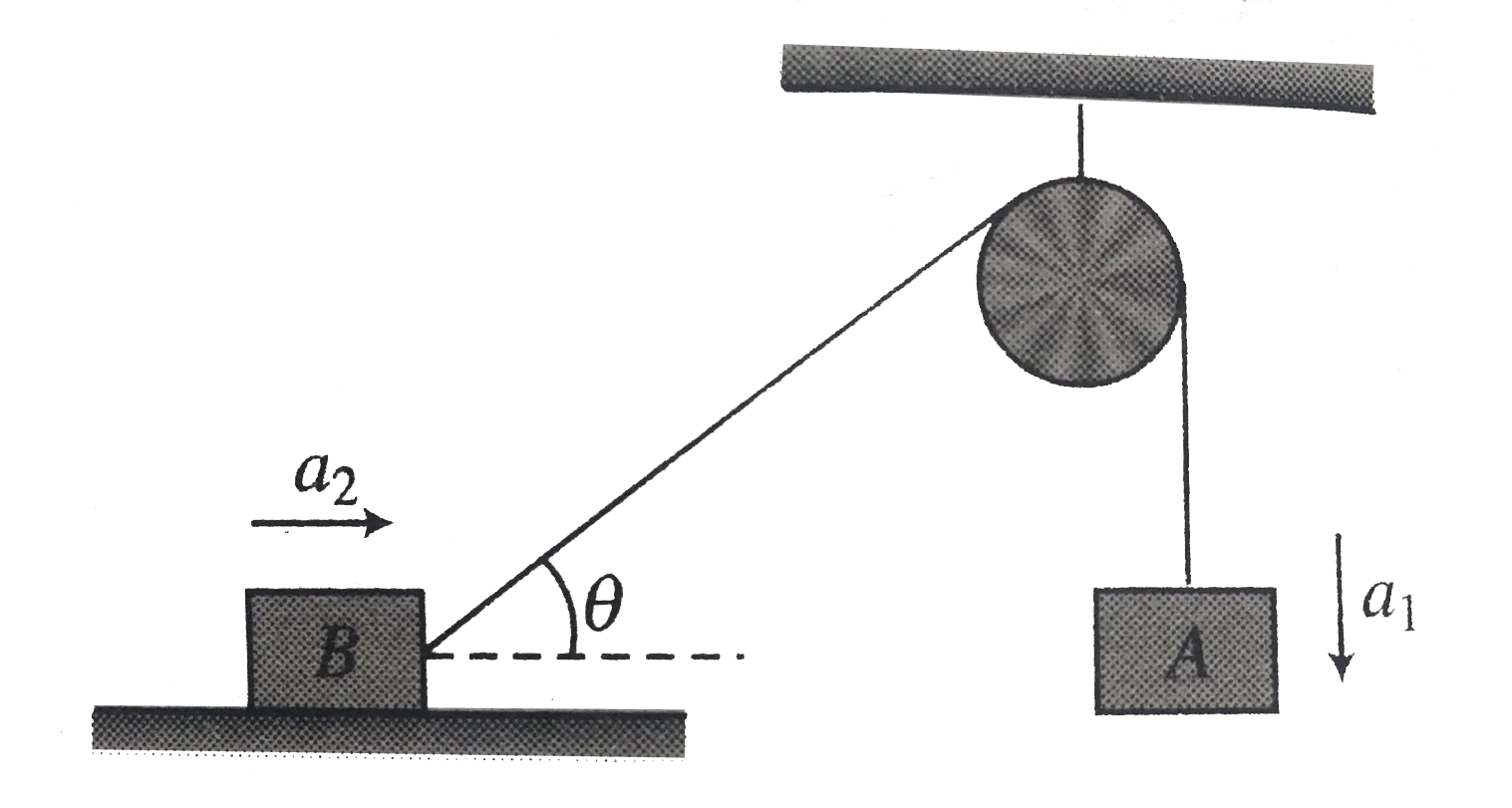
View SolutionIn the pulley-block arrangement shown in figure , find the relation between aA,aB and aC

View SolutionIn the pulley-block arrangement shown in figure , find the relation between aA,aB and aC

View SolutionThree blocks are placed as shown in figure. Mass of A, B and C are m1,m2,and m3respectively. The force exerted by block 'C' on 'B' is :-
View Solution
