A man standing on the roof a house of height h throws one particle vertically downwards and another particle horizontally with same velocity u. Find the ratio of their velocities when they reach the earth's surface.
To solve the problem, we need to analyze the motion of both particles separately and then find their velocities when they reach the earth's surface.
Step 1: Analyze the first particle (thrown vertically downwards)
- The first particle is thrown vertically downwards with an initial velocity u.
- The height from which it is thrown is h.
- We can use the kinematic equation to find the final velocity V1 of the first particle when it reaches the ground:
V2=u2+2gh
Here, g is the acceleration due to gravity (acting downwards), and h is the height.
- Rearranging gives us:
V1=√u2+2gh
Step 2: Analyze the second particle (thrown horizontally)
- The second particle is thrown horizontally with the same initial velocity u.
- Since it is thrown horizontally, its initial vertical velocity uy is 0.
- The horizontal component of its velocity Vx remains constant throughout its motion because there is no horizontal acceleration. Thus:
Vx=u
- For the vertical component, we can again use the kinematic equation to find the final vertical velocity Vy when it reaches the ground:
V2y=u2y+2gh
Since uy=0:
V2y=0+2gh⟹Vy=√2gh
Step 3: Calculate the resultant velocity of the second particle
- The total velocity V2 of the second particle when it reaches the ground can be found using the Pythagorean theorem, since it has both horizontal and vertical components:
V2=√V2x+V2y=√u2+(2gh)
Step 4: Find the ratio of the velocities
- Now we have both velocities:
V1=√u2+2gh
V2=√u2+2gh
- The ratio of their velocities V1 to V2 is:
V1V2=√u2+2gh√u2+2gh=1
Thus, the ratio of their velocities when they reach the earth's surface is:
Ratio=1:1
- The first particle is thrown vertically downwards with an initial velocity u.
- The height from which it is thrown is h.
- We can use the kinematic equation to find the final velocity V1 of the first particle when it reaches the ground:
V2=u2+2gh
- The second particle is thrown horizontally with the same initial velocity u.
- Since it is thrown horizontally, its initial vertical velocity uy is 0.
- The horizontal component of its velocity Vx remains constant throughout its motion because there is no horizontal acceleration. Thus:
- The total velocity V2 of the second particle when it reaches the ground can be found using the Pythagorean theorem, since it has both horizontal and vertical components:
- Now we have both velocities:
V2=√u2+2gh
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise 5.3
Explore 12 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise 5.4
Explore 11 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise 5.1
Explore 15 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
From the top of a tower body A is thrown up vertically with velocity u and another body B is thrown vertically down with the same velocity u.If VA and VB are their velocities when they reach the ground and tA and tB are their times of flight ,then
View SolutionA particle falls on earth :
(i) from infinity. (ii) from a height 10 times the radius of earth. The ratio of the velocities gained on reaching at the earth's surface is :
View SolutionA body is thrown horizontally with a velocity of v m/s from the top of a tower of height 2h reaches the ground in 't' seconds. If another body double the mass is thrown horizontally with a velocity 5v m/s from the top of another tower of height 8h it reaches the ground in a time of
View SolutionA particle is thrown with escape velocity ve from the surface of earth. Calculate its velocity at height 3 R :-
View SolutionA particle falls towards the earth from inifinity. The velocity with which it reaches the earth is surface is
View Solution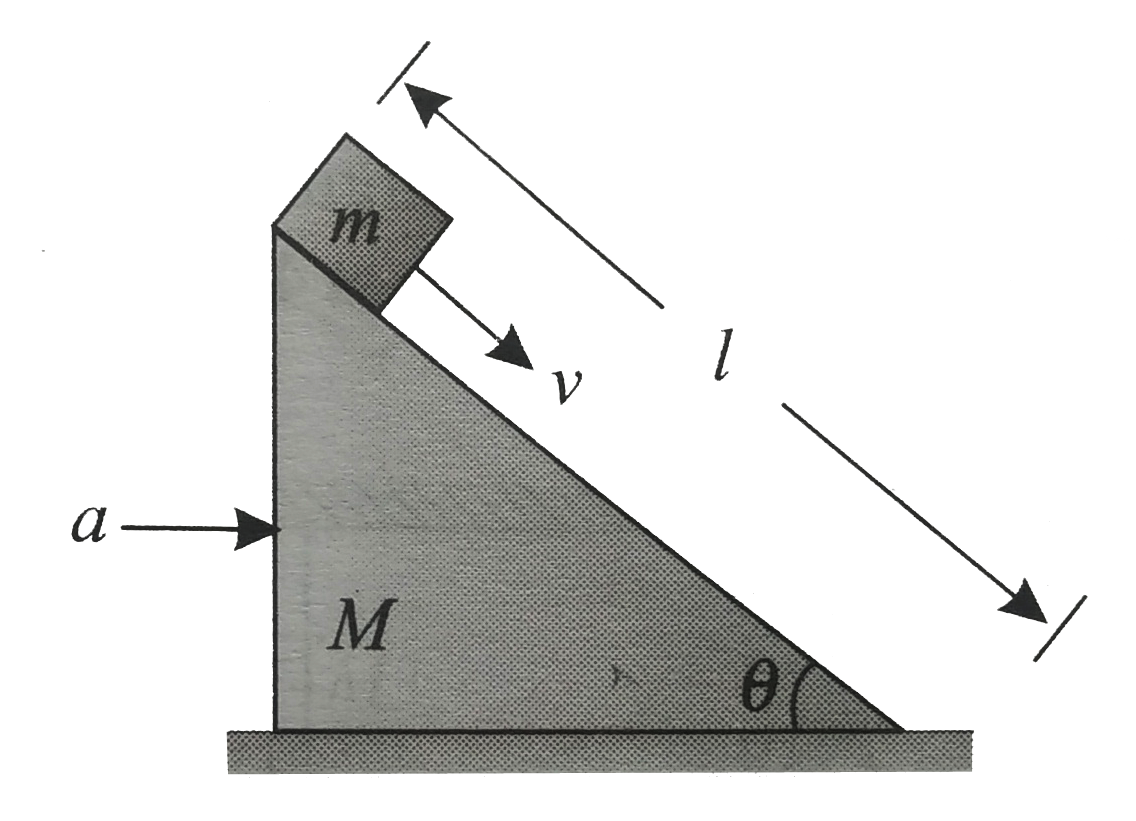
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:
View SolutionA particle (A) is dropped from a height and another particle (B) is thrown in horizontal direction with speed of 5 m/s from the same height. The correct statement is
View SolutionA person standing downward on a tower throws a stone vertically upward with a velocity u and drops another stone downward with same initial velocity. Which stone will strike the earth with a larger velocity ?
View SolutionA body is projected vertically upward from the surface of earth with a velocity sufficient to carry it to initially. Calculate the time taken by it to reach height h.
View SolutionA body falls freely from a height 'h' its average velocity when it reaches earth is
View Solution
